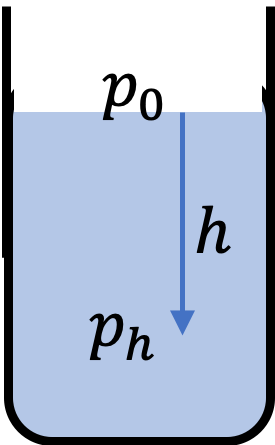
If the density of air didn’t vary with height, the pressure will vary with height in a linear way. This can be seen as follows. Suppose the atmosphere goes up to a height H. Since, there would be nothing above it, the pressure will be zero there. If we want pressure at height \(h\) from the sea level, we will just use the weight of air above \(h\text{,}\) which will be the air of a column of height \(H-h\text{.}\) Thus, the pressure at height \(h\) would be
\begin{equation*}
p_h = \rho_a g (H-h).
\end{equation*}
But, this is wrong! We will use a result from thermodynamics to make our point. In a gas, we can use ideal gas law, \(pV=Nk_BT\text{,}\) which can be also written as
\begin{equation*}
\rho = \dfrac{m}{k_B T}\, p,
\end{equation*}
where \(m \) is mass a gas molecule, which we can approximate to the mass of a nitorgen, \(N_2 \text{,}\) molecule, \(k_B \) a universal constant, called the Boltzmann constant, and \(T\) the temperature in kelvin. Let us use a \(y\) axis pointed up with origin at the sea level.
Then, at height, now given by coordinate \(y\text{,}\) the density and pressure are related by
\begin{equation}
\rho(y) = \dfrac{m}{k_B T}\, p(y),\tag{17.7}
\end{equation}
But, \(p(y)\) is just the pressure from all the air above \(y\text{.}\)
\begin{equation*}
p(y) = \dfrac{1}{A}\, g\, \int_{y}^{\infty} \rho(y) A dy,
\end{equation*}
from which we get the following differential relation.
\begin{equation*}
\dfrac{dp}{dy} = -g \rho(y),
\end{equation*}
which can be rewritten with the help of Eq.
(17.7) as
\begin{equation}
\dfrac{dp}{dy} = -\alpha p,\tag{17.8}
\end{equation}
where
\begin{equation}
\alpha = \dfrac{mg}{k_B T}.\tag{17.9}
\end{equation}
Eq.
(17.8) can be rearranged and then integrated from
\(y=0\) to
\(y=y\text{.}\)
\begin{equation*}
\int_{p_0}^{p(y)}\dfrac{1}{p} dp = -\int_0^y \alpha dy.
\end{equation*}
This gives
\begin{equation*}
\ln \dfrac{p(y)}{p_0} = -\alpha y,
\end{equation*}
which is solve for \(p\text{.}\)
\begin{equation}
p(y) = p_0\, e^{-\alpha y}.\tag{17.10}
\end{equation}
This shows that the atmospheric pressure decreases exponentially with height \(y \text{,}\) and not linearly. The pressure drops by a factor of \(\frac{1}{e}\) when height from the sea level is \(\dfrac{1}{\alpha}\text{.}\) Based on this we get a physical interpretation for \(\alpha \text{:}\) constant \(\dfrac{1}{\alpha}\) is a length scale that characterizes how pressure varies with height.
An approximate value of \(\alpha\) can be obtained by using mass of a nitrogen molecule as a proxy for an air molecule. At temperature \(27^{\circ}\text{C}\) or \(300\text{K}\text{,}\) we find
\begin{equation}
\alpha=-\frac{mg}{k_B T} = \frac{1}{9,000\ \text{m}}. \tag{17.11}
\end{equation}
Therefore, for every 9,000 meters, the air pressure drops by a factor \(\dfrac{1}{e}\) or approximately one-third of its value. Of course, this gives us only a rough estimate of the physical situation since we have assumed both the temperature and \(g\) constant over such great distances from the Earth, neither of which is correct in reality.