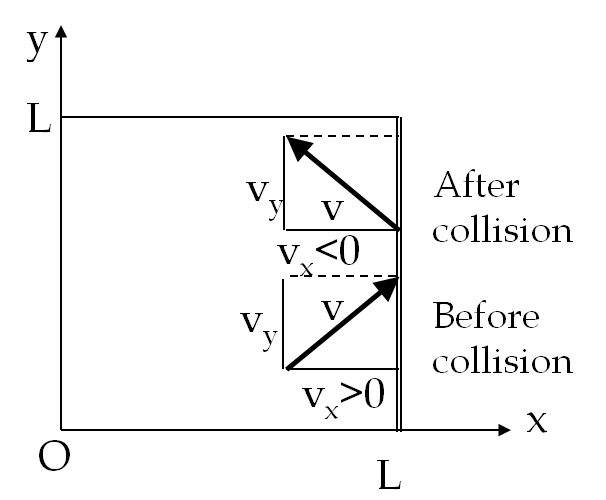
Looking at the wall at \(x=L\) again, we find the calculations of the simple model for a single molecule goes through without much change except now we have \(v_x\) in place of \(v\) in the formulas. The number of collisions made by a molecule on the right wall only depends on the \(v_x\text{.}\) A random molecule will collide with all six walls because, in general, it will have all three components \(v_x\text{,}\) \(v_y\) and \(v_z\) non-zero. Therefore, the force on the right wall will be obtained by adding up the contributions from all \(N\) molecules with the following result.
\begin{equation*}
F_x^{net}= \dfrac{1}{L} \left( mv_{1x}^2 + mv_{2x}^2 +\cdots + mv_{Nx}^2 \right)\ \ \text{(net on right wall)},
\end{equation*}
where the subscripts \(1, 2, \cdots , N\) label the molecules. The quantity in parenthesis is related to the average of the square of the \(x\)-component of velocities of the molecules denoted as \(\langle v_x^2\rangle\text{.}\)
\begin{equation*}
\langle v_x^2\rangle = \dfrac{v_{1x}^2 + v_{2x}^2 +\cdots + v_{Nx}^2}{N}.
\end{equation*}
We will denote the average quantities by including them within angle brackets, \(\langle \dots\rangle\text{.}\) Therefore, the force exerted on the right wall by all molecules can be written more compactly as
\begin{equation}
F_x^{net}= \dfrac{m}{L} N \langle v_x^2\rangle \ \ \text{(net on right wall)}.\tag{27.3}
\end{equation}
Since, the velocities are assumed to be random, the average of square of the \(x\)-component of velocities must be equal to the corresponding \(y\) and \(z\)-averages, especially because \(N\) is very large in any macroscopic sample.
\begin{equation}
\langle v_x^2\rangle = \langle v_y^2\rangle = \langle v_z^2\rangle.\tag{27.4}
\end{equation}
Recall that the sum of squares of the \(x\text{,}\) \(y\) and \(z\)-component of velocity is equal to the square of the speed. Writing the speed of any one molecule as \(v\text{,}\) we have the following for each molecule.
\begin{equation*}
v_x^2 + v_y^2 + v_z^2 = v^2
\end{equation*}
Now, adding this equation for all molecules and dividing by the total number of molecules gives an identical relation for the average of square of the components of the velocity and the speed.
\begin{equation}
\langle v_x^2\rangle + \langle v_y^2\rangle + \langle v_z^2\rangle = \langle v^2\rangle.\tag{27.5}
\end{equation}
The average of the square of speeds is also called root-mean-squared speed, \(v_{rms}\text{.}\)
\begin{equation}
v_{\text{rms}}=\sqrt{\langle v^2\rangle}. \tag{27.6}
\end{equation}
\begin{equation}
\langle v_x^2\rangle = \langle v_y^2\rangle = \langle v_z^2\rangle = \dfrac{1}{3}v_\text{rms}^2.\tag{27.7}
\end{equation}
Using this relation in Eq.
(27.3) and noting that there is nothing special about any one wall, we find that the magnitude of force on any one of the six walls is give by the following.
\begin{equation}
|F^\text{net}|= \dfrac{1}{3L} N m v_\text{rms}^2.\tag{27.8}
\end{equation}
Dividing by area of the wall, we obtain the pressure in terms of the root-mean squared speed.
\begin{equation}
p = \dfrac{|F^\text{net}|}{L^2} = \dfrac{N}{3V}\, mv_\text{rms}^2.\tag{27.9}
\end{equation}
The only difference between this formula and Eq.
(27.1) is that
\(v\) now is
\(v_\text{rms}\text{.}\)