Velocity and Speed

Section 4.3 Velocity and Speed

Subsection 4.3.1 Average Velocity

The rate at which position changes with time gives us information about the flow of motion. A simple measure of the rapidity of a motion, both how fast the movement occurs and in which direction the movement is taking place, is obtained by dividing the displacement vector \(\Delta \vec r\) by the interval \(\Delta t\text{.}\) The ratio is called average velocity during that interval.

\begin{equation} \vec v_{\text{av}} = \dfrac{\Delta \vec r}{\Delta t} .\tag{4.13} \end{equation}

Since \(\Delta \vec r \) is a vector and we are dividing it by a simple number, average velocity, \(\vec v_{\text{av}} \) will also be a vector. Just as other vectors, we can represent velocity by an arrow of appropriate size in appropriate direction. We can slso study it analytically in terms of its components with respect to some axes or in the magnitude-direction form.

Noting that displacement \(\Delta \vec r \) has the components \((\Delta x, \Delta y, \Delta z) \text{,}\) Eq. (4.13) gives us relation for each cmponent of average velocity to the correspnding displacement.

\begin{equation*} v_{\text{av},x}= \dfrac{\Delta x}{\Delta t}, \ \ v_{\text{av},y}= \dfrac{\Delta y}{\Delta t}, \ \ v_{\text{av},z}= \dfrac{\Delta z}{\Delta t}. \end{equation*}

From the components, we can deduce the magnitude and direction as we would do for any other vector as illustrated in Example 4.18.

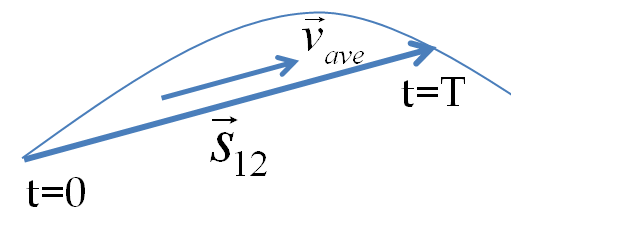
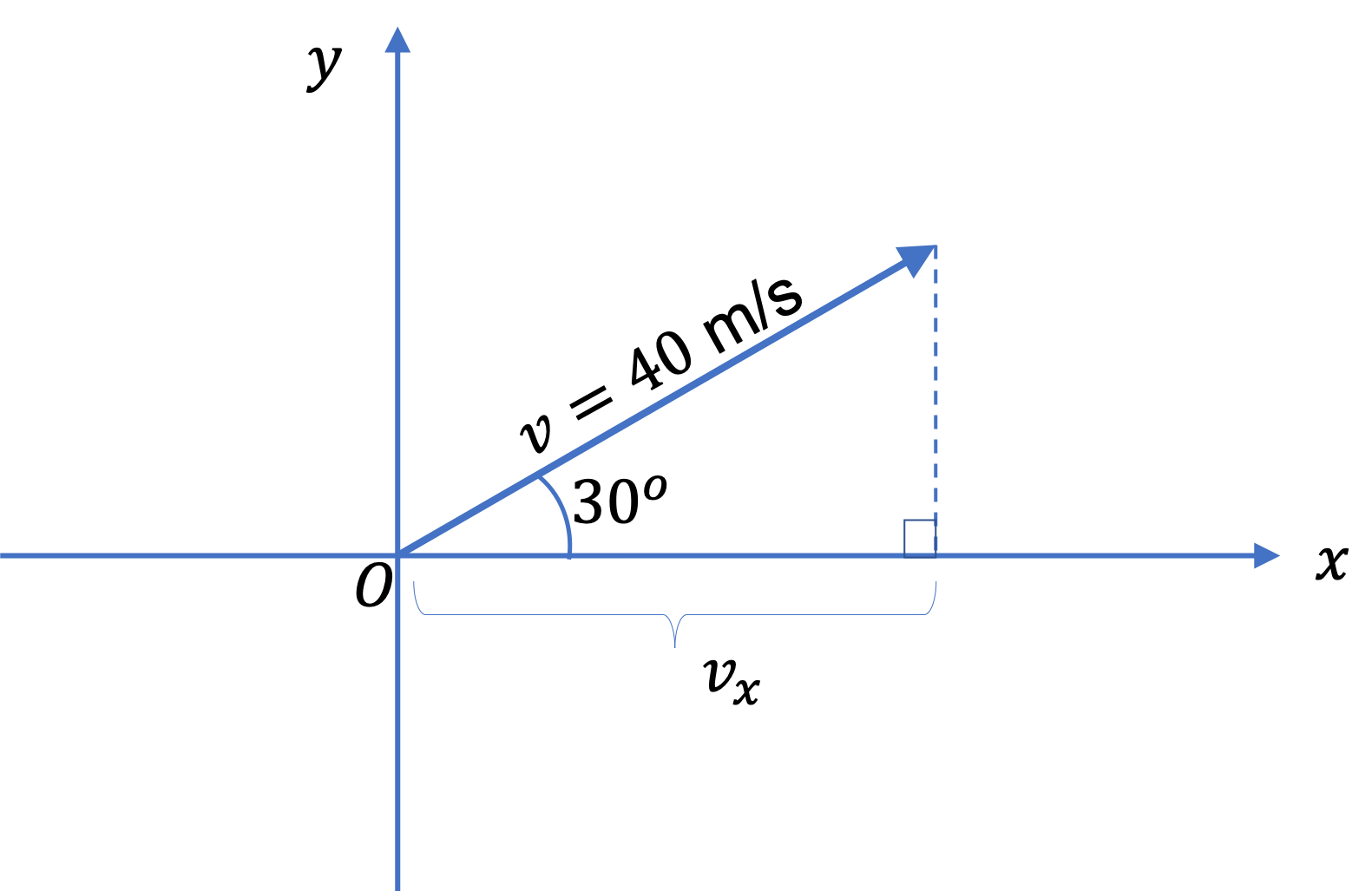
Example 4.16. Average Velocity of a Motion in a Straight Line.

A train starts from Boston at \(7:00\) AM and goes towards New York City. In the first \(2\) minutes, the train moves on a straight track facing West and covers a direct distance of \(3000\) m from the starting point. What is the average velocity?

Solution.

The displacement is \(3000\) m due West in interval \(2\) min. The magnitude of the average velocity will be

\begin{equation*} v_{av} = \frac{3000\text{ m}}{2\times 60 \text{ s}} = 25\,\text{m/s}. \end{equation*}

The direction will be same as the direction of the displacement since the interval was a positive number. That is the average velocity is \(25\,\text{m/s}\) towards West.

Example 4.17. Average Velocity Components and Coordinate Choice.

For simplicity, consider an object moving in a straight line such as a train on a straight track. When we place a coordinate system such that its \(x\)-axis falls on the straight line of motion, the displacement will be a vector that can point either towards the positive \(x\)-axis or towards the negative \(x\)-axis only. Therefore, displacement in this coordinate system can be written entirely as a scalar multiple of the unit vector \(\hat u_x\text{,}\) which will mean that the average velocity has only the \(x\)-component \(v_{av,x}\)

\begin{equation*} \vec v_{av} = v_{av,x} \hat u_x. \end{equation*}

If \(v_{av,x} \gt 0\text{,}\) then the average velocity will be in the same direction as the vector \(\hat u_x\text{,}\) i.e. towards the positive infinity of the \(x\)-axis, and if the \(v_{av,x} \lt 0\text{,}\) then the average velocity will be in the direction opposite to that of the vector \(\hat u_x\text{,}\) i.e. towards the negative infinity of the \(x\)-axis. The direction towards the positive infinity of the \(x\)-axis is also referred to as moving to the right or moving toward the positive \(x\)-axis. Similarly we say moving to the left or towards the negative \(x\)-axis for the direction towards negative infinity of the axis.

We will use similar descriptions of motions on a straight line, if we happen to use a coordinate system oriented such that its \(y\) or \(z\)-axis coincides with the straight line where the motion takes place.

Example 4.18. Average Velocity from Displacement and Duration.

An ant is crawling randomly on the floor. At some time \(t = 0 \text{,}\) the ant is at coordinates \((20\text{ cm}, -30\text{ cm}) \) and some time later, at \(t = 20\text{ sec} \text{,}\) it is at \((-10\text{ cm}, 10\text{ cm}) \text{.}\) What is the average velocity in (a) the component form and (b) in the magnitude-direction form?

Answer.

(a) \((-1.5\text{ cm/s}, 2.0\text{ cm/s} ) \text{,}\) (b) \(2.5\text{ cm/s},\ 53.1^{\circ}\) clockwise from negative \(x \) axis.

Solution 1. a

We first find the displacement vector in the component form.

\begin{equation*} \Delta x = -10-20 = -30\text{ cm},\ \ \Delta y = 10-(-30) = 40\text{ cm}. \end{equation*}

Therefore, the components of the average velocity are

\begin{align*} \amp v_{\text{av},x} = \dfrac{\Delta x}{\Delta t} = \dfrac{-30}{20} = -1.5\text{ cm/s}. \\ \amp v_{\text{av},y} = \dfrac{\Delta y}{\Delta t} = \dfrac{40}{20} = 2.0\text{ cm/s}. \end{align*}

Therefore, \(\vec v_{\text{av}} = (-1.5\text{ cm/s}, 2.0\text{ cm/s} ) \text{.}\)

Solution 2. b

The magnitude and angle from components can be found from the same formulas that relate \((x, y) \) to \((r, \theta)\text{.}\)

\begin{align*} \amp v_{\text{av}} = \sqrt{1.5^2 + 2^2} = 2.5\text{ cm/s}. \\ \amp \theta = \tan^{-1}\left( \dfrac{2}{-1.5}\right) = -53.1^{\circ}. \end{align*}

Now, we interpret the angle to get the direction. Note that the point \((-1.5, 2) \) is in the second quadrant. Therefore, the direction is in a clockwise angle of \(53.1^{\circ}\) from the negative \(x \) axis.

Checkpoint 4.19. Average Velocity of a Motion in a Vertical Plane.

A projectile is flying through the air in a plane. At \(t=0\text{,}\) the projectile is at the origin of a coordinate system, and at \(t=T\text{,}\) the coordinates of the projectile are \((X,Y,0)\text{.}\) What is the average velocity of the projectile over the time interval \(0\) to \(T\text{?}\)

Solution.

The analytic viewpoint of average velocity tells us that we can construct the average velocity vector from its components, which we can readily find here.

\begin{align*} \amp v_x^{ave} = \frac{X-0}{T-0} = \frac{X}{T} \\ \amp v_y^{ave} = \frac{Y-0}{T-0} = \frac{Y}{T}\\ \amp v_z^{ave} = \frac{0-0}{T-0} = 0 \end{align*}

Therefore, the average velocity has the following representation in the given coordinate system.

\begin{equation*} \vec v_{ave} = \left( \frac{X}{T} \right)\hat u_x + \left( \frac{Y}{T} \right)\hat u_y. \end{equation*}

The magnitude and direction of the average velocity can be determined as usual from the components. The magnitude of the average velocity is

\begin{equation*} v_{ave} = \frac{\sqrt{X^2+Y^2}}{T}. \end{equation*}

Since, the motion occurs in a plane, one angle will be sufficient to specify the direction of the vector. The angle \(\theta\) from the positive \(x\)-axis in the \(xy\)-plane is given by

\begin{equation*} \theta=\arctan{\left( \frac{Y}{X} \right)}. \end{equation*}

This is the angle we usually specify when we want to give direction of a vector in the \(xy\)-plane.

Subsection 4.3.2 Average Speed

Often we are interested in the total distance traveled over some time interval and not necessarily in the direction of the motion. For instance, if you travel by car between two cities, the road will not always point in the same direction. The distance you must travel will be more than the direct distance between the cities. Let \(D\) be the actual distance moved in total time \(T\text{,}\) then the ratio \(D/T\text{,}\) called the average speed is a measure of how fast the distance was covered. We will denote average speed by \(v_{s,av}\text{.}\)

\begin{equation} \boxed{v_{s,av} = \frac{D}{T}.}\tag{4.14} \end{equation}

Average speed and magnitude of average velocity may be very different, especially in a motion where there are changes in direction. An extreme example will be a motion where an object returns to the original place after some time - the magnitude of average velocity in this case will be zero but average speed will not be zero.

Example 4.21. Average Speed versus Average Velocity.

Google maps shows that a road trip from Boston to Los Angeles will cover \(4800 \text{ km}\) and take \(48 \text{ hr}\text{.}\) If you were to dig a direct tunnel through the Earth between Boston and Los Angeles, you would find that the direct distance is approximately \(4100 \text{ km}\text{.}\)

(a) What is the average speed for the trip in km/h? (b) What is the average velocity for the trip?

Answer.

(a) \(100\text{ km/hr}\text{,}\) (b) \(84\text{ km/h}\) in the direction in tunnel from Boston to Los Angeles.

Solution 1. a

To obtain average speed, we divide the actual distance, as given by the road trip distance, by time.

\begin{equation*} v_s = \dfrac{4800 \text{ km}}{48 \text{ hr}} = 100\text{ km/hr}. \end{equation*}

Solution 2. b

Average velocity \((\vec v_{\text{ave}})\) is a vector - so, we need to specify both the magnitude and direction.

The direction here is simple to state: it is along the direct line from Boston towards Los Angeles, as in the tunnel.

The magnitude of the average velocity will be equal to the direct distance, not the distance on the road trip, divided by time.

\begin{equation*} v_{\text{ave}} = \dfrac{4100\text{ km}}{48\text{ hr}} = 84\text{ km/h}. \end{equation*}

Subsection 4.3.3 Instantaneous Velocity - Formal Definition

Average velocity and average speed do not tell us motion moment-by-moment. For that, Isaac Newton introduced the concept of instantaneous velocity based on concepts of limit and infinitesimal intervals.

If you find average velocity using Eq. (4.13) for different interval values, i.e., different values of \(\Delta t\) in, say, from \(t\) to \(t+\Delta t\) interval, you will find that you get different magnitude and directions of average velocities. Newton noticed that, as \(\Delta t\) become increasingly small, the differences in average velocities become less and less pronounced in a well-defined way such that it is possible to define a unique velocity in the limit \(\Delta t\rightarrow 0\text{.}\) Furthermore, \(\Delta t\rightarrow 0\) limit also makes \(t\) to \(t+\Delta t\) interval to be of “zero size”, thus giving us information about motion at instant \(t\).

Denoting the instantaneous velocity vector by \(\vec v \) and the position vector as \(\vec r\) we can write the definition of instantaneous velocity formally by

\begin{equation} \vec v = \lim_{\Delta t \rightarrow 0} \dfrac{\vec r\left(\text{at } (t+\Delta t)\right) - \vec r\left(\text{at } t\right)}{\Delta t} \equiv \frac{d\vec r}{dt}.\tag{4.15} \end{equation}

The magnitude of instantaneous velocity gives us the speed at that instant. Although, we noted above that average speed and magnitude of average velocity may be different, but instantaneous speed and magnitude of instantaneouos velocity are always same since averaging in Eq. (4.15) is over an infintesimal time interval.

Eq. (4.15) is an abstract definition, which we can make more accessibale by looking at the components. Denoting \(\vec r\left(\text{at } (t+\Delta t)\right) - \vec r\left(\text{at } t\right)\) by \(\Delta \vec r \equiv (\Delta x, \Delta y, \Delta z)\text{.}\)

\begin{align*} \amp v_x= \lim_{\Delta t \rightarrow 0}\dfrac{\Delta x}{\Delta t} \equiv \frac{dx}{dt},\\ \amp v_y= \lim_{\Delta t \rightarrow 0}\dfrac{\Delta y}{\Delta t} \equiv \frac{dy}{dt},\\ \amp v_z= \lim_{\Delta t \rightarrow 0}\dfrac{\Delta z}{\Delta t} \equiv \frac{dz}{dt}. \end{align*}

These components of velocity are also called \(x\)-, \(y\)-, and \(z\)-velocity respectively. In a previous chapter, we have studied one-dimensional motion, where only one of them was non-zero. For general motion, you can expect all of them to be nonzero and you would need to keep track of them all.

Numbers \(v_x\text{,}\) \(v_y\text{,}\) and \(v_z\) you would obtain this way are the Cartesian components of the vector \(\vec v\text{.}\) Thus, once we have obtained \((v_x, v_y, v_z)\text{,}\) we can deduce the magnitude and direction of the velocity vector as we do for any vector. For instane, magnitude of velocity, i.e., speed, will simply be the magnitude of the vector.

\begin{equation} v = \sqrt{v_x^2 + v_y^2 + v_z^2}.\tag{4.16} \end{equation}

For direction of \(\vec v\text{,}\) we will use either polar angle in case of a motion in a plane, or spherical cordinate angles in case of motion in a three-dimensional space.

Subsubsection 4.3.3.1 Computing Derivatives from the Slopes of Tangents

In experiments we measure position at a finite number of instants and deduce the instantaneous velocity by making a plot of position versus time. You will now see that the components of velocity, i.e. \(v_x(t)\text{,}\) \(v_y(t)\) and \(v_z(t)\text{,}\) can be determined from the plots of \(x\) vs \(t\text{,}\) \(y\) vs \(t\) and \(z\) vs \(t\) respectively, since the derivative of a function is also equal to the slope of the tangent of the curve when the function is plotted along the ordinate (the vertical axis) and time along the abscissa (the horizontal axis).

Let us look at an example of the \(x\)-component of velocity from the \(x\) vs \(t\) plot. Consider the graphs of a function \(x(t)\) given in Figure 4.22. Suppose we are interested in the \(x\)-component of velocity at \(t=1\) sec. The slopes of the secants joining a point of the curve before \(t=1\) sec and a point after \(t=1\) sec give the \(x\)-component of the average velocity for various time intervals. The figure shows that, as we examine shorter and shorter time intervals, the secants tend to become parallel to the tangent to the curve at \(t=1\) sec, the instant of interest. Therefore, the slope of the tangent will equal the instantaneous rate of change. This gives us another way of computing derivatives, which is particularly important for relating to experimental results.

\begin{equation} \frac{dx}{dt} = \textrm{Slope of the tangent to the }x \textrm{ vs } t \textrm{ curve}.\tag{4.17} \end{equation}

(for accessibility) — Figure 4.22. The \(x\)-component of the instantaneous velocity at the instant \(t=1\) sec is equal to the slope of \(x\) vs \(t\) curve at \(t=1\) sec. The slopes of the secants for various time intervals around \(t=1\) sec give average velocities in those time intervals. This figure shows visually that the slopes of secants change as we zero in near the instant of interest, eventually the secant becomes parallel to the tangent to the curve.

Remark 4.23. No Sharp Corners in \(x\) vs \(t\) plot..

Note that in a plot of \(x\text{,}\) \(y\text{,}\) or \(z\) vs \(t\text{,}\) there cannot be sharp corners since the velocity of an object cannot change abruptly. That is, the velocity at an instant before the corner must be arbitrarily close to the velocity an instant after the corner. In the limit of infinitesimal interval around the corner, the velocity obtained at an instant before a corner will not equal the one for an instant after the corner. Therefore, the plots of coordinates versus time must be smooth at all points, meaning that \(x(t)\text{,}\) \(y(t)\) and \(z(t)\) are smooth functions of \(t\text{,}\) not just continuous functions.

Example 4.24. Velocity From Slope.

The position of a box in a one-dimensional motion is recorded by placing the \(y\)-axis on the line of motion. The data is plotted as a \(y\) vs \(t\) plot and shown in Figure 4.25. Find the \(y\)-component of velocity at \(t=1\) sec, \(3\) sec, \(5\) sec, and \(7\) sec.

Solution.

The plot of \(y\) vs \(t\) is a segment-wise straight line, which makes finding slopes easier. We do not need to draw any tangents since the tangent to a straight line is the straight line itself. The slopes at \(t=1\) sec and \(t=3\) sec are equal, \(v_y = 1\) m/s. The slope at \(t=5\) sec is zero since the line is flat and rise is zero. Therefore at \(t=5\) sec, \(v_y = 0\text{.}\) Finally, the slope is negative at \(t=7\) sec. The \(y\)-coordinate changes by \(-2\) m in \(3\) sec steadily. This gives \(v_y = -2/3\) m/s.

Example 4.26. Velocity from Position.

A ball is thrown in the air. With \(x\)-axis horizontal and \(y\)-axis pointed vertically up, the position of the ball at time \(t\) is given by

\begin{equation*} x = 30 t,\ \ y = 40 t - 5 t^2. \end{equation*}

Here \(x\) and \(y\) are units of m and \(t\) is units of s. (a) What is its initial velocity? (b) What is its velocity at \(t= 5\text{ s}\text{.}\)

Answer.

(a) \(50\text{ m/s}\text{,}\) counterclockwise \(53^\circ\) from positive \(x\)-axis , (b) \(10\sqrt{10}\,\text{m/s}\text{,}\) \(18.4^\circ\) clockwise from positive \(x\)-axis.

Solution 1. a

By taking derivatives of \(x\) and \(y\) we get the components of vbelocity to be

\begin{equation} v_x = \frac{dx}{dt} = 30,\ \ \ v_y = \frac{dy}{dt} = 40 - 10 t.\tag{4.18} \end{equation}

At initial instant \(t=0\text{.}\) Therefore, we have the following values of components at initial time.

\begin{equation*} v_x = 30, \ \ \ v_y = 40. \end{equation*}

Therefore, the mangitude of the velocity is

\begin{equation*} v = \sqrt{v_x^2 + v_y^2} = \sqrt{30^2 + 40^2} = 50\text{ m/s}, \end{equation*}

and the direction is in the forst quadrant countercloclockwise from the positive \(x\)-axis at angle

\begin{equation*} \theta = \tan^{-1}\left( 40/30 \right) \approx 53^\circ. \end{equation*}

Solution 2. b

We already have components of velocity at an arbitrary instant in Eq. (4.18). Therefore magnitude of velocity is

\begin{equation*} v = \sqrt{ 30^2 + \left( 40 - 10 t\right)^2 }. \end{equation*}

For \(t=5\text{ s}\text{,}\) this gives

\begin{equation*} v = 10\sqrt{10}\,\text{m/s}. \end{equation*}

The counterclockwise angle from the positive \(x\)-axis is

\begin{equation*} \theta = \tan^{-1}\left( (40 - 10 t)/30 \right), \end{equation*}

which can become negative if the ball continues to fall for a time \(t > 4\text{ s}\text{.}\) For \(t=5\text{ s}\text{,}\) it is

\begin{equation*} \theta = \tan^{-1}\left( -10/30 \right) = -18.4^\circ. \end{equation*}

This angle is in 4th quadrant and is clockwise \(18.4^\circ\) from positive \(x\)-axis.

Example 4.27. Velocity as a Vector in a Horizontal-Vertical Plane.

Suppose a cannon ball is fired with a speed \(50 \text{ m/s}\) at an angle \(40^{\circ}\) with the horizontal direction. A coordinate system is chosen such that the \(x \) axis points horizontally and the positive \(y \) axis points vertically up. What are the \(x \) and \(y \) components of the velocity vector?

Answer.

\(v_x = 38\text{ m/s} \text{,}\) \(v_y = 32\text{ m/s} \text{.}\)

Solution.

Project a vertical line from the tip of the arrow to the \(x \) axis (with the tail of the arrow at the origin. The length on the \(x \) axis from origin is the \(v_x \text{.}\) Trigonometry tells us that this should be hypotehnuse (which equal to the speed \(v \)) times cosine.

\begin{equation*} v_x = v\, \cos\, \theta = 50\text{ m/s}\, \cos\, 40^{\circ} = 38\text{ m/s}. \end{equation*}

Similiarly, the projection on the \(y \) axis gives \(v_y = v\, \sin\, \theta\text{,}\) which evaluates to \(32\text{ m/s} \text{.}\)

Example 4.28. Computing Velocity Components from Magnitude and Direction - 2D.

A cannon ball is fired at an angle of \(30^{\circ} \) above the horizon at a speed of \(40\text{ m/s}\text{.}\) Consider positive \(x \) axis horizontally in the general direction the ball will fly and positive \(y \) axis vertically up. (a) Draw the vector in the \(xy\) plane and from its projections on the axes, identify the components on the diagram. (b) What are the \(x\) and \(y\) components of the velocity vector?

Answer.

(b) \(34.64\text{ m/s}, 20\text{ m/s}\text{.}\)

Solution 1. a

Lets draw the vector first and identify the \(x \) and \(y \) components in the diagram so that we can identify the trig we need. For clarity I will show only the \(x \) component.

The diagram illustrates the projection on the \(x \) axis to get the \(x \) component \(v_x\text{.}\) We draw the velocity vector with tail at the origin, and then we drop a perpendicular from the tip to each axis - figure shows only to \(x \) axis for clarity. You should do similarly for the \(y \) component.

Solution 2. b

We are going to omit units in the calculations, but put back the units in the answers. From the figure it is clear that

\begin{align*} v_x \amp = v \cos\theta = 40 \times \cos\, 30^{\circ} = 34.64\text{ m/s}. \end{align*}

Similarly,

\begin{align*} v_y\amp = v \sin\theta = 40 \times \sin\, 30^{\circ} = 20\text{ m/s}. \end{align*}

Example 4.29. Instantaneous Velocity from Slope - 1 Dimensional.

The figure below shows an example of calculation of the \(x \) component of instantaneous velocity from a plot of \(x \) vs \(t\text{.}\) To obtain \(v_x\) at an instant, say at \(t=t_1\text{,}\) we draw a tangent to the curve at \(t=t_1\) as shown in the figure.

The rise of the tangent line gives the change in position \(\Delta x\) along the axis and the run of the tangent gives the duration \(\Delta t\) for that change. Therefore, slope of the tangent line, obtained by dividing \(\Delta x \) by \(\Delta t \) gives the rate at which \(x \) coodinate changes at \(t_1\text{,}\) i.e, the \(v_x \) at \(t_1\text{.}\)

At time \(t_1\text{,}\) the slope of the tangent, i.e., \(v_x\text{,}\) is positive, meaning the velocity is pointed in the positive \(x \) direction for a one-dimensional motion on the \(x \) axis.

Just to remind you that velocity for one-dimensional motion on the \(x \) axis is \(\vec v = v_x \hat i\text{,}\) where \(\hat i\) is the unit vector pointed towards the positive \(x \) axis. Note that at time \(t_2 \) in the figure, the slope is zero, meaning that the \(v_x \) is zero there. At time \(t_3\text{,}\) the slope is negative, meaning the velocity will be pointed in the negative \(x \) axis direction for a one-dimensional motion.

I wish to emphasize here that an \(x \) vs \(t \) plot gives you only \(v_x \text{.}\) In a three-dimensional motion, you will need \(x \) vs \(t \) , \(y \) vs \(t \text{,}\) and \(z\) vs \(t \) so that you can deduce \(v_x \text{,}\) \(v_y \text{,}\) and \(v_z \) of velocity. You can then construct the magnitude and direction of the velocity vector from them.

Example 4.30. Computing Velocity from Position Graphs - 2 Dimensional.

A ball is rolling on the floor. The position of the ball is recorded as \((x,y)\) of a coordinate system. The \(z\) coordinate of the ball is always zero in this coordinate system and therefore ignored. The plots of \(x\) vs \(t\) and \(y\) vs \(t\) are displayed here. Find the velocity of the ball at (a) \(t = 3\text{ sec}\text{,}\) (b) \(t=5\text{ sec}\text{,}\) and (c) \(t=7\text{ sec}\text{.}\)

Answer.

(a) \((0.5\ \text{ m/s},\ 1.0\text{ m/s} )\text{,}\) (b) \((-0.5\text{ m/s},\ 0) \text{,}\) (c) \((-0.5\text{ m/s},\ -1.0\text{ m/s})\text{.}\)

Solution 1. a

The slope of the \(x \) vs \(t \) grasph at \(t = 3 \) is obtained by two points on the line through the \((t=3, x=1.5)\) point on the graph. Lets pick the second point on this line to be \((t=0, x=0)\text{.}\) Then we get

\begin{equation*} v_x = \dfrac{1.5-0}{3-0} \text{ m/s} = \dfrac{1}{2} \text{ m/s}. \end{equation*}

Similarly we pick two points on the line through \((t=3, y=1.0)\) point. Let the other point on this line be \((t=2, y=0)\text{.}\) This gives

\begin{equation*} v_y = \dfrac{1.0-0}{3-2} \text{ m/s} = 1.0 \text{ m/s}. \end{equation*}

Therefore, the velocity in component form in the \(xy\)-plane is \((0.5\ \text{ m/s}\text{,}\) \(1.0\text{ m/s} )\text{.}\)

Solution 2. b

Similary, we get \(v_x = -0.5\text{ m/s}\) and \(v_y = 0\text{.}\)

Solution 3. c

I got \(v_x = -0.5\text{ m/s}\) and \(v_y = -1.0\text{ m/s}\text{.}\)

Subsection 4.3.4 Direction of Instantaneous Velocity from Trajectory

If you can draw the path of the moving object in space, you will get some curvy trajectory in space. The direction of velocity at some instant, then is the direction of the tangent to this trajectory as shown in Figure 4.31.

Figure 4.31. The direction of velocity vector can be deduced from tangent to the path/trajectory of the object in space. The figure shows directions of velocity vectors at instants \(t_1 \) and \(t_2\text{.}\)

Example 4.32. Velocity of a Projectile at Different Points.

The trajectory of a projectile is shown in the figure below with the assumption that the initial velocity was \(80\text{ m/s}\) at the angle of \(72^{\circ}\) from the horizontal direction. The position of the projectile at successive \(1 \text{ sec}\) instants are shown in the figure

You can see that the direction as well as the magnitude of the velocity of the projectile changes with time. As the projectile rises, the distance covered in each subsequent second decreases as a result of slowing down. At the top of the trajectory, the projectile only has horizontal velocity since the vertical component of the velocity is zero there. The velocity is never pointed vertically straight down since the projectile always has a non-zero horizontal component of the velocity.

Exercises 4.3.5 Exercises

1. Magnitude and Direction from Components of a Velocity in the Third Quadrant.

Suppose a football is on a downward path. The \(x \) and \(y \) components of its velocity are \((-30\text{ m/s}, -40\text{ m/s}) \text{.}\) Find its magnitude and direction. Assume positive \(x\) axis points East and positive \(y \) axis points Up.

Hint.

Use formulas for \((r, \theta)\) in terms of \((x,y) \text{.}\)

Answer.

\(50\text{ m/s} \text{,}\) \(53.1^{\circ}\) South of West.

Solution.

The magnitude and angle of any vector are related to the components by the same formulas as \((r, \theta) \) for position vector are to \((x,y) \text{.}\) Therefore,

\begin{align*} \amp v = \sqrt{v_x^2 + v_y^2} = 50\text{ m/s}, \\ \amp \theta = \tan^{-1}\left(\dfrac{v_y}{v_x} \right) = 53.1^{\circ}. \end{align*}

We now need to interpret this angle to get the direction. The point \((-30, -40) \) is in the third quadrant, therefore, the direction is counterclockwise from the negative \(x \) axis. This gives the directioj to be \(53.1^{\circ}\) South of West. as shown in Figure 4.33.

2. The Components of Velocity in a Vertical Plane.

Suppose a cannon ball is fired with a speed \(v_0 \) at an angle \(\theta \) with the horizontal direction. A coordinate system is chosen such that the \(x \)-axis points horizontally and the \(y \)-axis points vertically up as shown in Figure 4.34 . What are the \(x \) and \(y \)-components to the velocity vector?

Solution.

The hypotenuse of the right-angled triangle \(\triangle OPQ \) has length equal to the magnitude of the velocity vector, and the sides \(OQ \) and \(PQ \) are the \(x \) and \(y \)-components, to be denoted as \(v_{0x} \) and \(v_{0y} \) respectively. Trigonometry yields the following expressions for the components immediately.

\begin{align*} \amp v_{0x} = v_0\cos\theta \\ \amp v_{0y} = v_0\sin\theta \end{align*}

3. Drawing Velocity Vectors in a Circular Motion.

Consider a child going in a circular path in a merry-go-round at a constant speed of \(5 \text{ m/s}\text{.}\) Draw a circle and show velocity vectors at four different points of the circle.

Hint.

Direction is tangent to the circle.

Answer.

see solution

Solution.

At each point, the velocity is tangent to the trajectory as shown in Figure 4.35.

Figure 4.35. Figure for Exercise 4.3.5.3.

4. (Calculus) Velocity from Position.

The position of a pendulum bob is given by \(\vec r = 5 \cos(t)\, \hat i + 5\sin(t)\, \hat j\) in units of m with units of second for \(t \text{.}\) Find the velocity of the bob at \(t = 2 \text{ s}\text{.}\)

Hint.

Take derivatives and evaluate at \(t=2 \text{ s}\text{.}\)

Answer.

\(v_x = -4.55 \text{ m/s, } v_y = -2.08 \text{ m/s}.\) or \(5.0\text{ m/s},\ 24^{\circ}\) counterclockwise from the negative \(x \) axis.

Solution.

Note that the position vector has given us the \(x(t) \) and \(y(t) \text{,}\) the coordinates of the pendulum bob as functions of time \(t \text{.}\) From these we can immediately obtain the \(v_x \) amnd \(v_y \text{,}\) the components of the velocity vector.

\begin{align*} \amp v_x = \dfrac{dx}{dt} = \dfrac{d}{dt}\left( 5\, \cos\,t\right) = -5\,\sin\,t\\ \amp v_y = \dfrac{dy}{dt} = \dfrac{d}{dt}\left( 5\, \sin\,t\right) = 5\, \cos\,t \end{align*}

Evaluating these for \(t = 2 \) gives the following once we put the units back in.

\begin{equation*} v_x = -4.55 \text{ m/s, } v_y = -2.08 \text{ m/s}. \end{equation*}

From this we get the magnitude of velocity to be \(5.0\text{ m/s}\) and angle with the \(x \) axis to be

\begin{equation*} \theta = \tan^{-1}\left( 2.08/4.55\right)= 24^{\circ}. \end{equation*}

Since the point \((-4.55, -2.08) \) is in the third quadrant, the direction of the velocity is \(24^{\circ} \) counterclockwise from the negative \(x \) axis.

Prev Top Next