Electrons in motion collide with fixed nuclei, other electrons, and vibrational excitations called phonons. As a result, a material heats up when a current flows through it. In this context, we refer conductors as resistors. The heating of resistors is responsible for such useful applications of electricity as the conventional electric oven and the light bulb.
The rate of heating of a resistor can be calculated by using the principle of conservation of energy. Suppose current
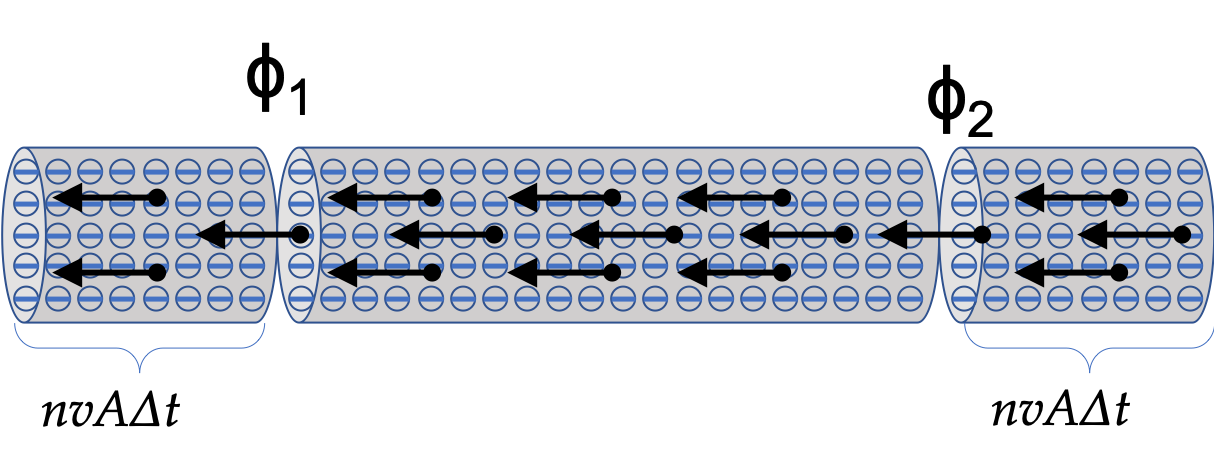
\(I\) flows through a cylindrical wire across which a voltage difference
\(\Delta \phi=\phi_1-\phi_2\) is maintained (
Figure 34.22). Let
\(n\) be the number of conduction electrons per unit volume and
\(v\) their average drift speed. Let
\(A\) be the area of cross-section and
\(R\) the resistance of the wire. As a result of the current in the wire, electrons in the wire will move a distance
\(v \Delta t\) in time
\(\Delta t\text{.}\)
What will be the change in energy of the segment of wire between points 1 and 2 in
Figure 34.22 during this interval? Notice that
\(nvA\Delta t\) electrons will enter the wire at potential
\(\phi_2\) and leave at potential
\(\phi_1\text{.}\) The entering electron at 2 will bring in energy equal to
\(-envA\Delta t \phi_2\) since the potential energy of a charge
\(q\) at a point of potential
\(\phi\) is equal to
\(qV\text{.}\) The outgoing electrons at 1 will take away energy equal to
\(-envA\Delta t \phi_1\text{.}\) The difference will be increase in energy of the segment between 1 and 2. This energy heats up wire with heat equal to
\begin{equation*}
\text{Heat} = -e n v A\Delta t \phi_2 - \left(- e n v A\Delta t \phi_1\right).
\end{equation*}
Therefore, the rate of heating of the wire segment, also called power dissipated in the wire, will be given by dividing heat by time. This gives
\begin{equation*}
P = e n v A \left( \phi_1 - \phi_2 \right).
\end{equation*}
The quantity \(e n v A\) is the rate of net charge flow in the wire, which is the current \(I\) in the wire. The difference \(\left( \phi_1 - \phi_2 \right)\) is the potential difference \(\Delta\phi\text{,}\) which is also denoted by voltage symbol \(V\text{.}\)
\begin{equation*}
P = I \Delta \phi = I\;V.
\end{equation*}
By using Ohm’s law \(V = I R\) we can rewrite power in alternate forms.
\begin{equation*}
P = I \Delta \phi = I V = I^2 R = \frac{V^2}{R}.
\end{equation*}
The SI unit of power is Watts (\(\text{W}\)), which is same as Joule/sec (J/s). In electrical units, \(1\text{ W}\) of power is equal to \(1\text{ VA}\text{,}\) or, \(1 \text{ A}^2\Omega\text{,}\) or, \(1 \text{ V}^2/\Omega\text{.}\)
\begin{equation*}
1\ \text{W} = 1\ \text{V.A} = 1\ \text{A}^2\Omega = 1\ \text{V}^2/\Omega = 1\ \text{J/s}.
\end{equation*}