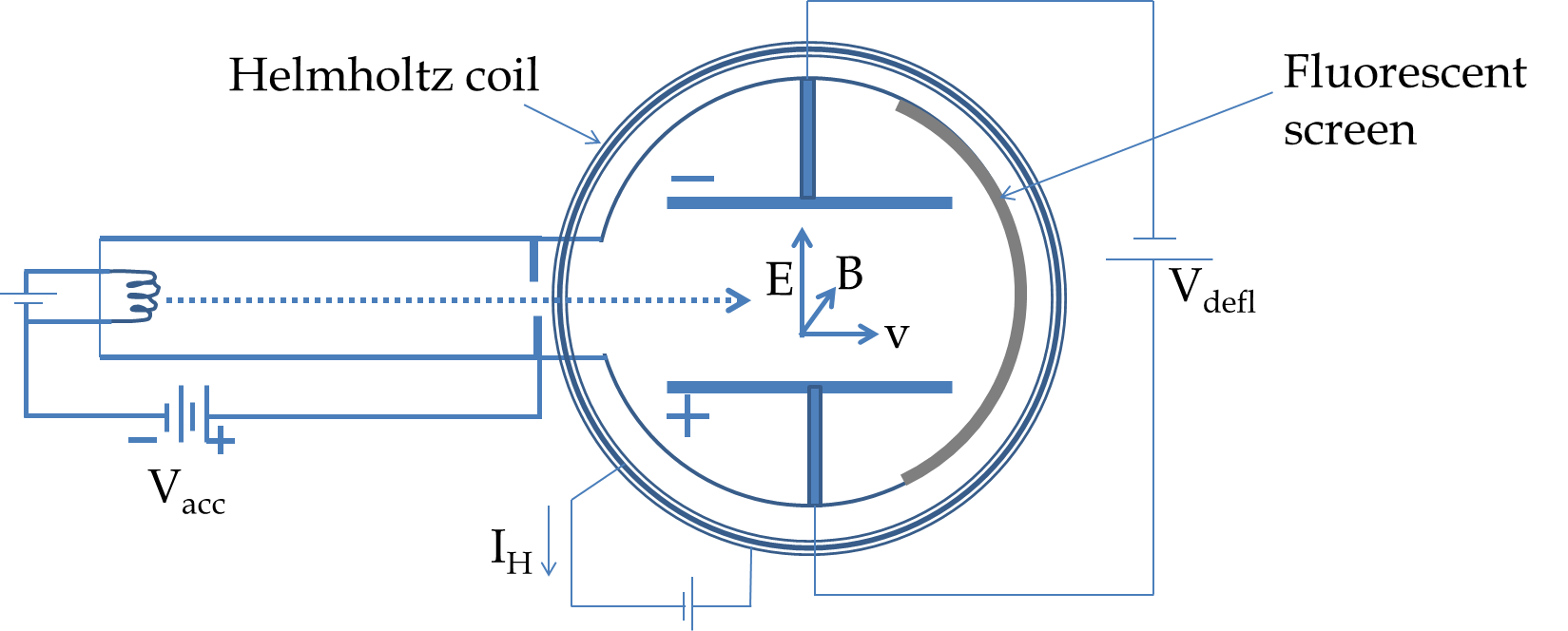
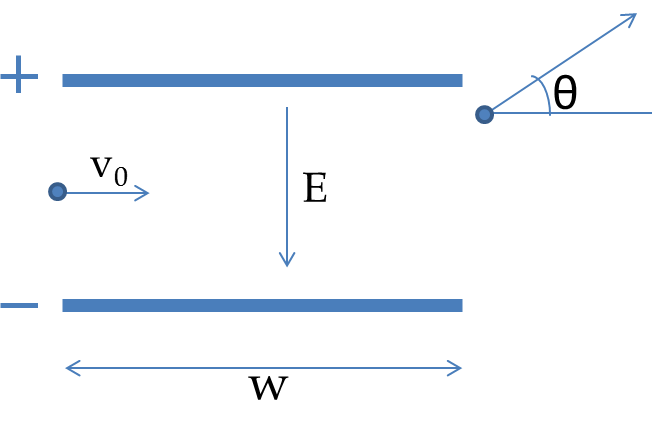
In an e/m experiment accelerating voltage \(V_{\textrm{acc}} = 3,000 \text{ V}\text{.}\) The accelerated electrons enter the evacuated chamber between the plates separated by a distance 5 cm. When a deviation voltage of \(V_{\textrm{d}} = 100 \text{ V}\) is applied across the plates, the electric force acts on the moving electrons over a distance of 10 cm. (a) What is the transverse displacement of the electron? (b) What is the angle at which the electrons will emerge from the space between plates?
Hint.
Ignore gravity and use constant acceleration.
Answer.
(a) \(\frac{1}{6}\:\textrm{cm}\text{,}\) (b) \(1.9^{\circ}\text{.}\)
Solution 1. (a)
We will refer to Figure 52.4 for calculations here. The acceleration part will be used to figure out the speed with which the electron will enter the deflection region. When the electron is moving between the plates, it has a constant force upward and gravity force downward. We will assume the electric force to be far greater than the force of gravity so that we can ignore the later. This gives a constant acceleration situation between the plates.
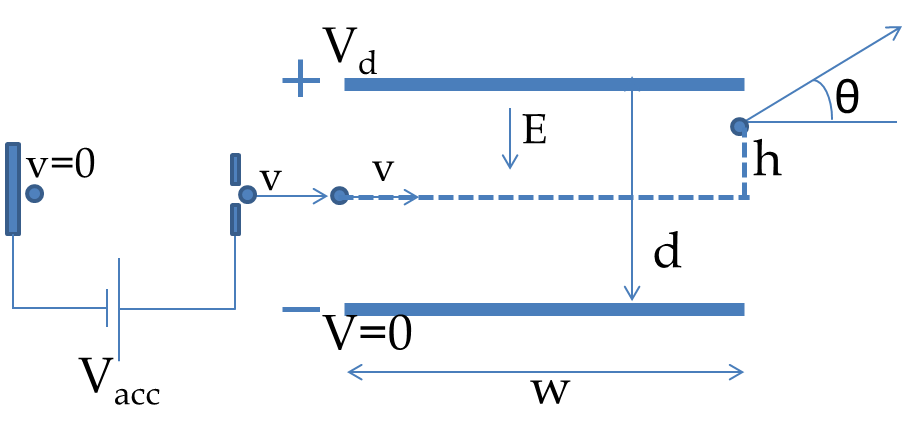
Using the consant acceleration equations will give us the vertical displacement when the horizontal displacement is \(w = 10\text{ cm}\text{.}\) We will first work out the solution in symbolic form before we put in the numbers. The acceleration phase gives
\begin{equation*}
\frac{1}{2} m v^2 = eV_{acc},\ \ \ v = \sqrt{\frac{2 eV_{acc}}{m}}.
\end{equation*}
For calculations of motion in the space between plates let \(x\)-axis be pointed horizontally in the figure and \(y\)-axis pointed vertically up. Ignoring gravity, the acceleration of the electron when it is between plates will have only \(y\)-component,
\begin{equation*}
a_y = \frac{eE}{m},
\end{equation*}
with
\begin{equation*}
E = \frac{V_d}{d}.
\end{equation*}
(a) To find the transverse displacement we apply constant velocity condition along the \(x\)-axis and constant acceleration condition along the \(y\)-axis yielding
\begin{equation*}
w = v t,\ \ h = \frac{1}{2} a_y t^2.
\end{equation*}
Eliminating \(t\) gives
\begin{equation*}
h = \frac{1}{2} a_y (w/v)^2.
\end{equation*}
Now, plugging in \(v\) and \(a_y\) from above we get the vertical displacement to be
\begin{equation*}
h = \frac{1}{2} \frac{eV_d}{m d} \:\frac{mw^2}{2 eV_{acc}} = \frac{1}{4} \frac{V_d w^2}{dV_{acc}}.
\end{equation*}
The numerical values given here gives
\begin{equation*}
h = \frac{1}{4} \frac{100\:\textrm{V}\times (10\:\textrm{cm})^2}{(5\:\textrm{cm})\times 3,000\:\textrm{V}} = \frac{1}{6}\:\textrm{cm}.
\end{equation*}
Solution 2. (b)
(b) To find the direction in which the particle will be moving when it emerges from the space between the plates, we need the direciton of the velocity when the electron is there. We know the \(x\)-component to be \(v\text{.}\)
\begin{equation*}
v_x = v = \sqrt{\frac{2 eV_{acc}}{m}}.
\end{equation*}
The \(y\)-component will be
\begin{equation*}
v_y = a_y t = \frac{eV_d}{m d}\: \frac{w}{v}.
\end{equation*}
Therefore, the angle \(\theta\) at which the electron will be headed will be
\begin{equation*}
\tan\theta = \frac{v_y}{v_x} = \frac{eV_d}{m d}\: \frac{w}{v} \times \sqrt{\frac{m}{2 eV_{acc}}} = \frac{V_d w}{2 V_{acc} d}.
\end{equation*}
For the numerical values given we get
\begin{equation*}
\tan\theta = \frac{100\:\textrm{V}\times 10\:\textrm{cm} }{2\times 5\:\textrm{cm}\times 3,000\:\textrm{V}} = \frac{1}{30}.
\end{equation*}
Therefore,
\begin{equation*}
\theta \approx \frac{1}{30}\:\textrm{rad} = 1.9^{\circ}.
\end{equation*}