Section 38.4 Magnetic Force on Moving Charges
When you shoot a charged particle between the poles of a magnet you find that its trajectory bends as illustrated in Figure 38.4.1. That is, the direction of the velocity changes, which means that a charged particle has non-zero acceleration when moving in a magnetic field. By multiplying this acceleration by the mass of the particle, you can quantify the magnetic force on the particle.
By experimenting on particles of different charges, you find that the force is proportional to the magnitude of of the charge \(Q\text{.}\) Similarly, you can the study dependence on velocity of the particle \(\vec v\) and strength and direction of the magnetic field \(\vec B\text{.}\) These studies tell us that magnetic force \(\vec F_m\) is a vector cross product between velocity and magnetic field vectors.
We can write this more explictily by replacing the vector product by using angle \(\theta\) between the velocity vector \(\vec v\) and the direction magnetic field \(\vec{B}\text{.}\)
The direction of the force is already included in the cross product in Eq. (38.4.1). More commonly, we use visual aid shown in Figure 38.4.3 and Figure 38.4.4 to help obtain the direction.
To use the method illustrated in Figure 38.4.3, place the velocity and magnetic field vectors in one plane and sweep from velocity towards magnetic field vector with right hand; magnetic force on charge is directed towards the thumb and perpendicular to the plane of velocity and magnetic field.
Alternately, to use the method illustrated in the right panel of Figure 38.4.4, orient your right palm such that velocity is in the direction of the thumb and magnetic field towards any other finger; magnetic force on the particle will be coming out and perpendicular to the palm.
Clearly, magnetic force on a moving charge has complicated directional characteristics. For instance, if you shoot a positive particle from the bottom as in Figure 38.4.5, the an inward force on the particle will curve the trajectory to bring the particle inside. A negatively charged particle, on the other hand, will be pushed out on a curved trajectory.
Subsection 38.4.1 Operational Definition of Magnetic Field
Since acceleration of a particle is measurable, we can obtain a quantitative value fo force by multiplying the measured acceleration by the mass of the particle. Therefore, we can use magnetic force law, Eq. (38.4.1), to quantify magnetic field by measured \(Q\text{,}\) \(\vec v\text{,}\) and \(\vec F_m=m\vec a\text{.}\) This gives us the following operational definition of the magnetic field.
Magnetic field \(B\) is equal to one unit of magnetic field if force on a particle of charge \(1\text{ C}\) moving at speed \(1\text{ m/s}\) perpendicularly to the field experiences a force of magnitude \(1\text{ N}\text{.}\)
This unit of magnetic field is called Tesla, which is denoted by letter \(\text{T}\text{.}\)We can write Tesla in terms of fundamental units as \(\text{kg/A.s}\text{.}\) You can express Tesla in various other ways, such as \(\text{V.s/m}^2\text{.}\)
It turns out that 1 Tesla is too large a unit for geophysical measurements, and another unit called Gauss (\(\text{G}\)) is in common use, where 10,000 Gauss = 1 Tesla.
Earth's magnetic field is approximately \(0.5\text{ Gauss}\) while magnetic field of a refrigerator magnet is around \(1\text{ Tesla}\text{.}\) Magnetic field used in an Magnetic Resonance Imaging (MRI) machine is around \(2\text{ Tesla}\text{.}\) Some typical values of magnetic fields in nature and lab are given in Table 38.4.6 so that you can get a feel for the order of magnitude in various situations. As you can see magnetic field in nature varies over \(18\) orders of magnitude, from less than \(10^{-10}\text{ T}\) in the interstellar space to more than \(10^8\text{ T}\) in neutron stars.
| Location | Magnetic Field (\(\text{T}\)) |
| Neutron star surface | \(10^8\) |
| Superconducting magnet | \(5\) |
| Small bar magnet | \(1\) |
| Earth's Surface | \(0.5 \times 10^{-4}\) |
| Interstellar space | \(10^{-10}\) |
Subsection 38.4.2 Lorentz Force on Electric Charges
A charged particle can experience two forces, electric and magnetic forces, that are proportional to the amount of charge. The net force on an electric charge is called Lorentz force, or electromagnetic force, which is just a vector sum of the electric and magnetic forces on the charge.
Thus, net electromagnetic force \(\vec F_{em}\) on a charged particle of charge \(Q\) and velocity \(\vec v\) at a particular location, where electric field is \(\vec E\) and magnetic field \(\vec B\text{,}\) is given by
Note that the sign of charge \(Q\) is important here for determining the direction of the force. The motion of a charged particle in an environment, where both electric and magnetic fields exist, is determined as usual by setting up Newton's second law of motion.
In order to study the motion of an electric charge \(Q\) in a given electromagnetic environment, you can use Lorentz force in Newton's second law of motion if its speed is not relativistic, i.e., \(v \lt\lt c\text{,}\) where c is the speed of light in vacuum. For unchanging mass \(m\text{,}\) we will have the following equation.
where \(\vec F_\text{other}\) denotes the net non-electromagnetic force on the particle, such as the gravitational force.
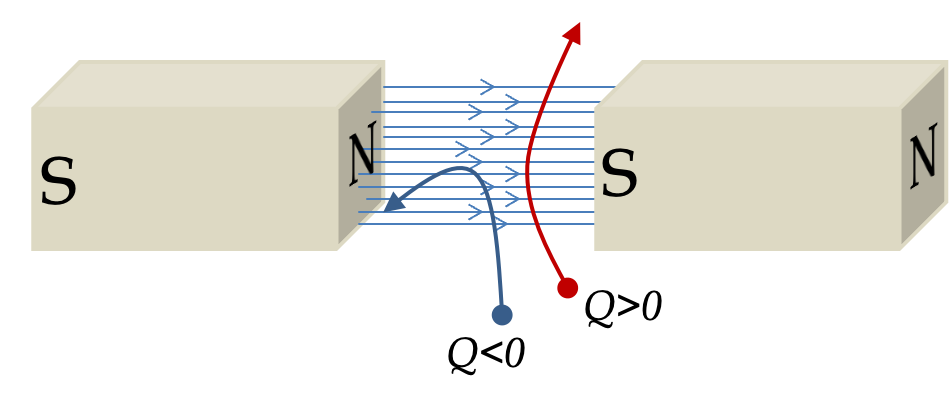
Checkpoint 38.4.7. Practicing Right-Hand Rule for Magnetic Force.
Find the direction of missing vector, either velocity, magnetic field, and magnetic force on the particle. Use a dot in a circle for pointing out of page and an \(\times\) inside a circle for pointing in the page. (Some answers have infinite number of possible directions. In those cases describe the complete answer, and an example correct direction.)
Use right hand rule.
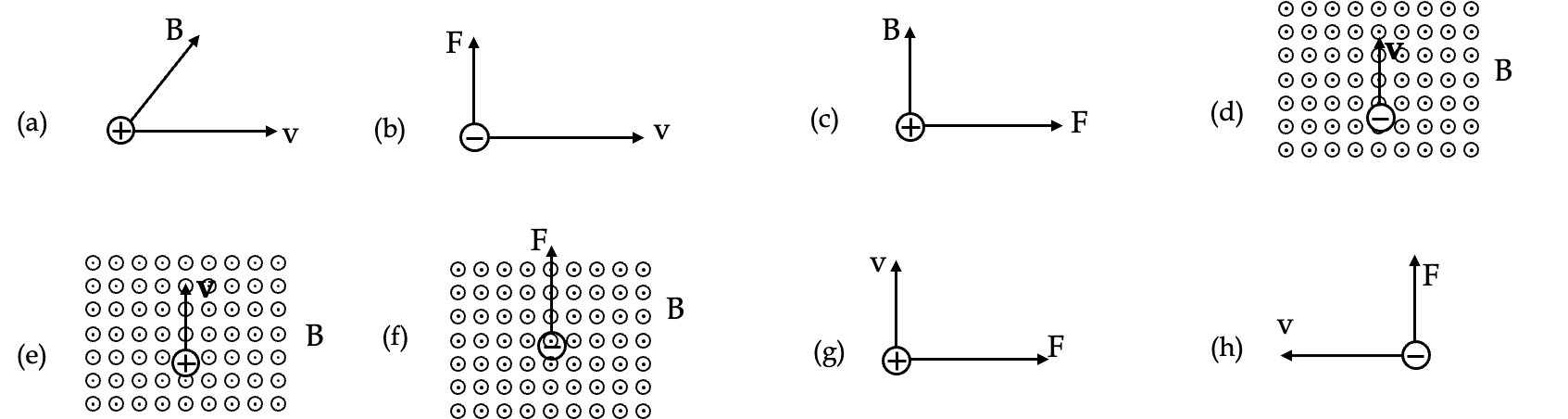
See solution.
- \(\bigodot \: \vec F\text{.}\)
- \(\bigotimes \: \vec B\text{.}\)
- \(\bigotimes \: \vec v\text{.}\)
- \(\stackrel{F}{\longleftarrow}\text{.}\)
- \(\stackrel{F}{\longrightarrow}\text{.}\)
- \(\stackrel{v}{\longrightarrow}\text{.}\)
- \(\bigodot \: \vec B\text{.}\)
- \(\bigotimes \: \vec B\text{.}\)