Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 43.10 Fundamentals of Optics Bootcamp

Exercises Exercises

Spectrum and Photons

1. Number of Photons in a Light Source.
Follow the link: Example 43.3.

Ray Optics versus Wave Optics

2. Deciding Between Wave Optics and Geometric Optics.
Follow the link: Exercise 43.2.1.

Speed of Light

Photometry and Radiometry

6. Luminosity of a Laptop Monitor at the Eye.
Follow the link: Exercise 43.5.2.
8. Radiant Intensity and Luminous Intensity of the Sun from Irradiance.
Follow the link: Exercise 43.5.4.

Optical Media

9. Speed and Wavelength of Light in Glass.
Follow the link: Example 43.20.
11. Wavelength of Light in Various Transparent Media.
Follow the link: Exercise 43.6.3.2.

Laws of Geometrical Optics

12. Rotation of Reflected Light upon Rotation of Mirror.
Follow the link: Exercise 43.7.3.1.
15. Lateral Displacment of a Ray when Traversing a Rectangular Plate.
Follow the link: Exercise 43.7.3.4.
16. Separation of Two Rays of Different Frequencies when Traversing a Rectangular Plate.
Follow the link: Exercise 43.7.3.5.

Bending of Light at Plane Interface

18. Deviation of a Ray Through an Equilateral Traingular Prism.
Follow the link: Exercise 43.8.4.1.

Miscellaneous

23. Speed of Light in Fizeau’s Experiment.
Refer to the Fizeau’s experiment shown in Figure 43.6. Prove that the speed of light will be equal to \(2\,n\,N\,d\text{,}\) where \(N\) is the total number of teeth in the wheel, \(n\) is the rotation rate of the wheel in number of revolutions per second when the returned light passes through the next opening in the wheel, and \(d\) is the distance from the apparatus to the mirror.
Hint.
Equated the time for back and forth of ray to the time to rotate to bring next opening of the wheel to line up.
Answer.
See solution.
Solution.
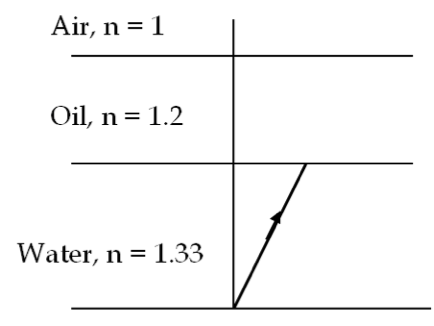
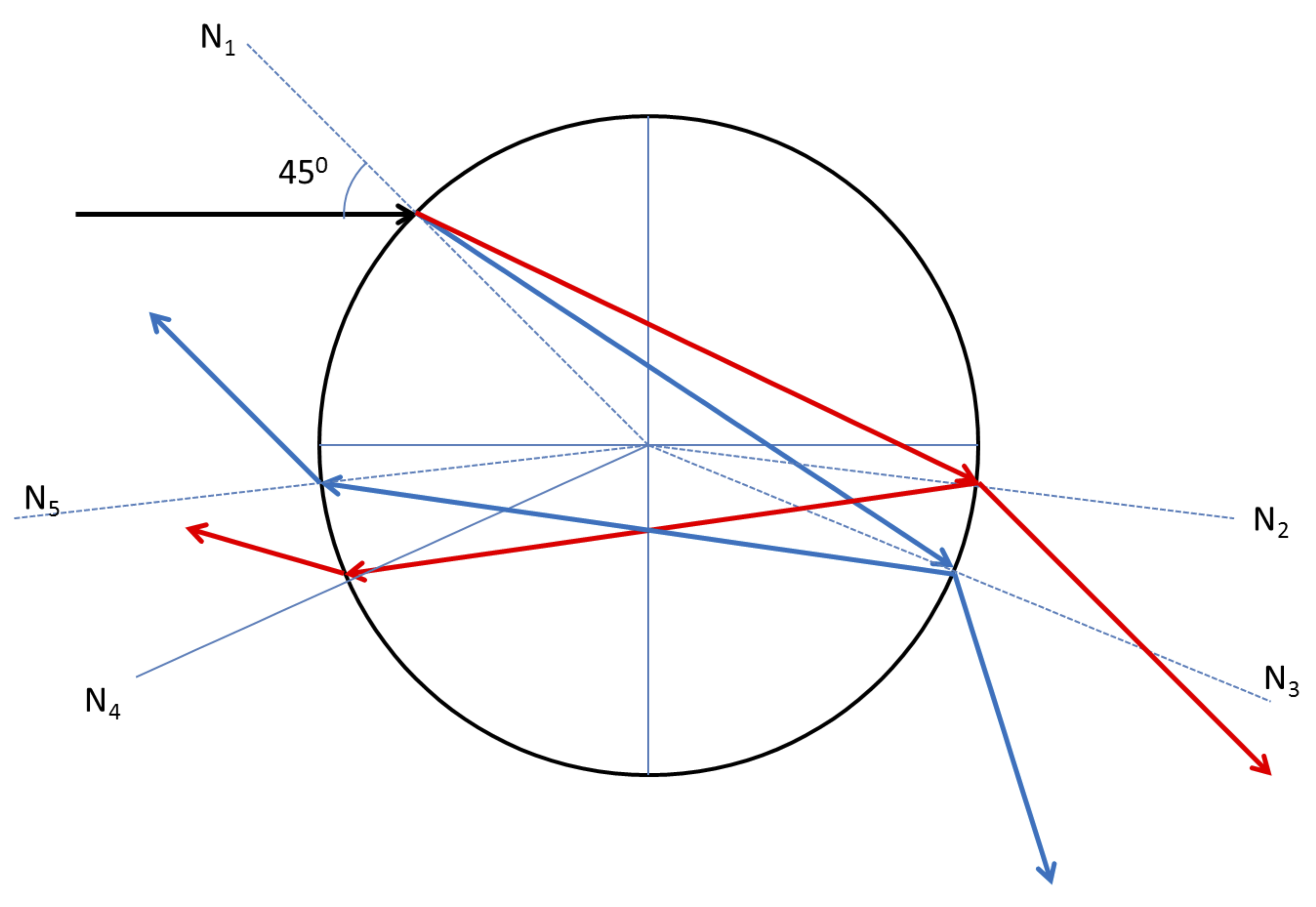
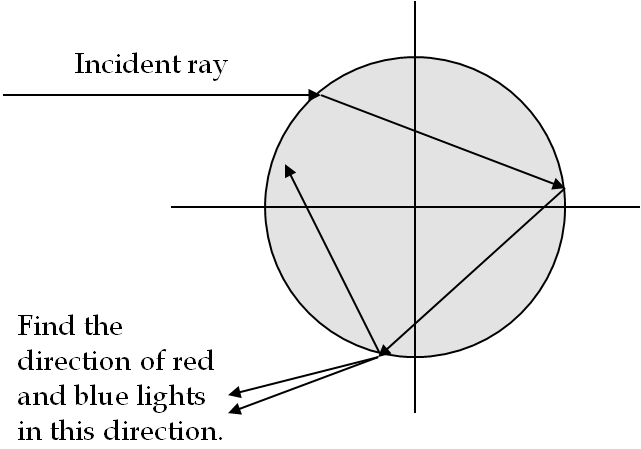
Using the symbol \(v\) for the speed of light, we find that the time for light to return to the wheel will be
\begin{equation*} \Delta t = \dfrac{2d}{v}. \end{equation*}
When we look at the motion of the wheel, during this time the wheel needs to rotate so that its the time between the subsequent openings in the wheel in the path of the light. In 1 sec the wheel will rotate through \(n\times N\) teeth. Therefore, the time between teeth will be
\begin{equation*} \Delta t' = \dfrac{1}{nN}. \end{equation*}
Equating \(\Delta t\) with \(\Delta t'\) gives
\begin{equation*} \dfrac{2d}{v} = \dfrac{1}{nN},\ \ \Longrightarrow\ \ v = 2\, d\, n\,N. \end{equation*}
24. Speed of Light in Michelson’s Experiment.
Refer to the Michelson’s apparatus for measuring the speed of light shown in Figure 43.8. Prove that the speed of light will be equal to \(16nd\text{,}\) where \(n\) is the rotation rate of the octagon mirror in the number of revolutions per second, and \(d\) is the distance from rotating mirror to the fixed mirror on the Lookout Mountain. Ignore the distance between the curved mirror and the flat mirror on the Lookout Mountain.
Hint.
Equate time for light to return to time for wheel to rotate by \(\dfrac{1}{8}\) of a turn.
Solution.
Using the symbol \(v\) for the speed of light, we find that the time for light to return to the rotating wheel will be
\begin{equation*} \Delta t = \dfrac{2d}{v}. \end{equation*}
When we look at the motion of the rotating wheel the time to rotate \(\dfrac{1}{8}\) of the full rotation will be
\begin{equation*} \Delta t' = \dfrac{1}{8}\times \dfrac{1}{n}. \end{equation*}
Equating \(\Delta t\) with \(\Delta t'\) gives
\begin{equation*} \dfrac{2d}{v} = \dfrac{1}{8n},\ \ \Longrightarrow\ \ v = 16nd. \end{equation*}
25. Ray of Light Through a Layer of Water and a Layer of Oil.
A small light bulb is at the bottom of a tank that has a layer of water and a layer of oil as shown in Figure 43.42. Find the path of the ray shown as it comes out in the air. Use a protractor to measure the angle of incidence. If you do not have a protractor, use angle of incidence equal to \(27^{\circ}\text{.}\)
Figure 43.42. Figure for Exercise 43.10.25.
Hint.
We use a protractor to find the angle of incidence at the water/oil interface.
Answer.
\(\theta_{\textrm{oil}} = 30^{\circ}\text{,}\) \(\theta_{\textrm{air}} = 37^{\circ}\text{.}\)
Solution.
The incidence angle turns out to be approximately \(27^{\circ}\text{.}\) Using Snell’s law at this interface we find that the angle of refraction for the given ray will be \(30.2^{\circ}\text{.}\) Since the interfaces are parallel, the angle of incidence at the oil/air interface is also \(30.2^{\circ}\text{.}\) Now, an application of Snell’s law at the oil/air interface gives the angle of refraction in air to be \(37^{\circ}\text{.}\)
26. Tracing Ray Through a Circular Prism.
A ray of light consisting of a red and a blue light is incident on a glass circular plate parallel to a diameter. If the refractive indices of red and blue lights for the given glass are \(1.5\) and \(1.55\) respectively, find the first two places where rays come out of the glass plate and the directions of the red and blue lights.
Hint.
Apply Snells’s law. The normal at each point of the circle is the radial line passing through center of the circle.
Solution.
Let us take a ray as shown in the figure and work out the angle of refraction. then, we draw rays as shown. When you have figured out the direction use a protractor to draw the ray till it meets the interface again and work out the Snell’s law for the exiting directions.
Figure 43.43. Figure for Exercise 43.10.26.
27. Separation for Colors when Traversing Through Raindrop.
(a) Trace the separation of a mixture of red and blue light rays in air when they strike a spherical drop of water shown in Figure 43.44. Use the following refractive indices for the red and violet lights in water as \(1.33\) and \(1.343\) respectively.
(b) How can you apply the results of this problem to understand rainbow?
Figure 43.44.
PrevTopNext
Found typo?