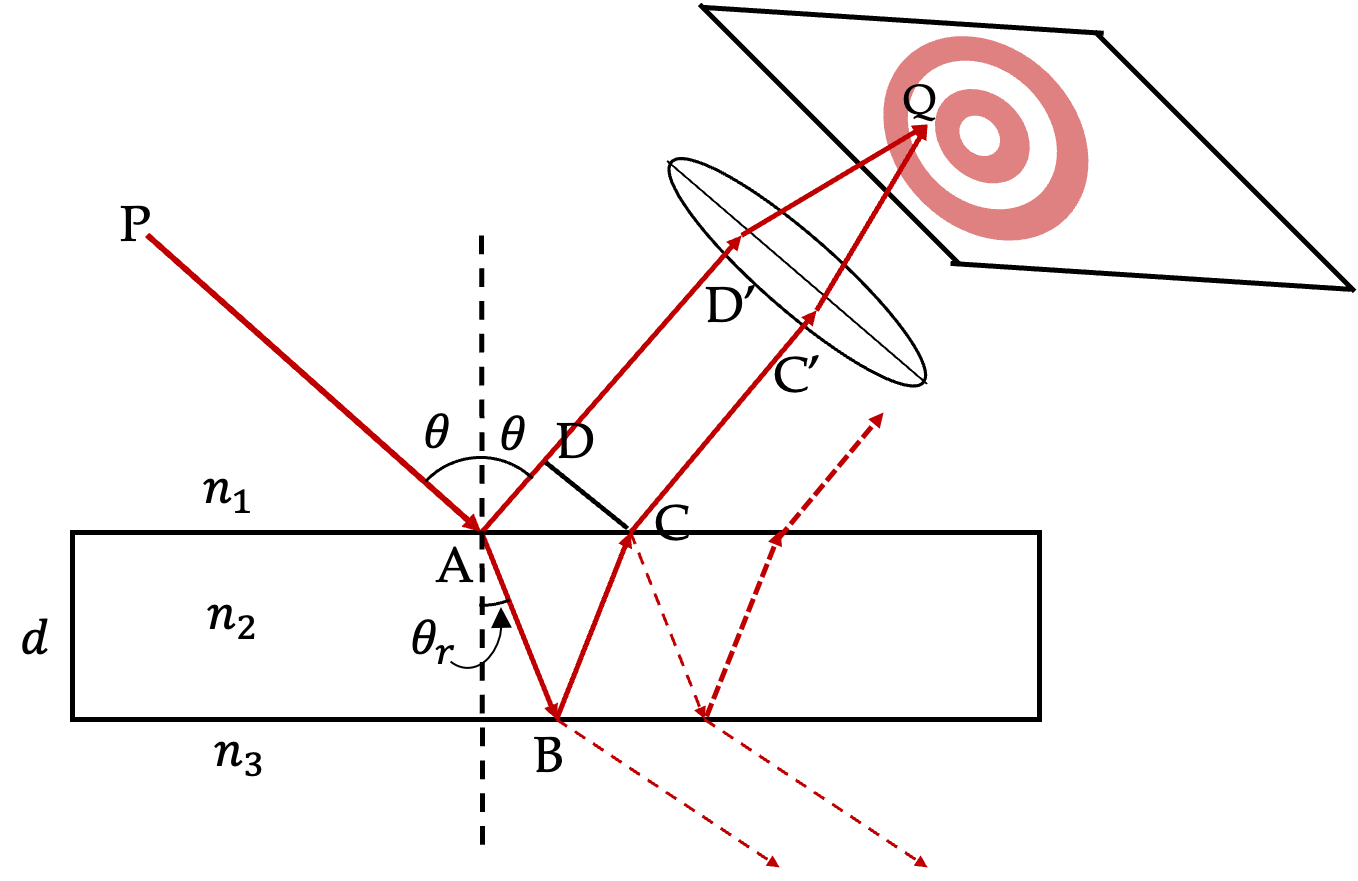
To find the phase difference in the two paths, we trace them so that we can locate phase changing reflections and appropriate path lengths starting from their common point P before any reflection occurs. Note that although PA part is common to both, but there is a difference between immediately before A and immediately after A in the two. So, you can imagine P to be as close to A as possible, but just before the reflection. This will give us the following phase difference \(\Delta_{12}\text{.}\)
\begin{align*}
\Delta_{12}\amp = (\text{phase change for reflection at A?} \\
\amp \ \ \ \ \ \ \ + \text{phase change for path AD})\\
\amp \ \ \ \ - ( \text{phase change for path AB}\\
\amp \ \ \ \ \ \ \ \ \ \ \ + \text{phase change for reflection at B?}\\
\amp \ \ \ \ \ \ \ \ \ \ \ + \text{phase change for path BC}).
\end{align*}
In the present case, the reflection at A causes a phase change of \(\pi\) radians since \(n_1\lt n_2\text{,}\) but the reflection at B does not have any phase change since \(n_2 \gt n_3\) - make sure you understand these comparisions in terms of first medium and second medium for each reflection event.
Now, we can find the phase change for traveling a distance AD in the first medium by noting that phase of a wave changes by \(2\pi\) radians when it travels one wavelength in the medium. We must be careful here and use the correct wavelength for each path since waves are traveling in different media. We are using \(\lambda_1\) and \(\lambda_2\) for the wavelength in the two media. Note that although the frequency of light is same in the two media, the wavelength will be different in the two media because speed of the wave depends on the refractive index.
\begin{align*}
\amp
\lambda_1 = \frac{v_1}{f} = \frac{c}{n_1 f}\\
\amp
\lambda_2 = \frac{v_2}{f} = \frac{c}{n_2 f}
\end{align*}
Therefore, we will have the following relation between the wavelengths.
\begin{equation*}
n_2 \lambda_2 = n_1 \lambda_1.
\end{equation*}
Hence, phase changes over the two paths are as follows.
\begin{align*}
\amp
\text{phase change over AD}= \frac{\text{AD}}{\lambda_1}\times 2\pi.\\
\amp
\text{phase change over AB}= \frac{\text{AB}}{\lambda_2}\times 2\pi =
\frac{n_2}{n_1} \frac{\text{AB}}{\lambda_1}\times 2\pi.\\
\amp
\text{phase change over BC}= \frac{\text{BC}}{\lambda_2}\times 2\pi =
\frac{n_2}{n_1} \frac{\text{BC}}{\lambda_1}\times 2\pi.
\end{align*}
Therefore phase difference between the two waves will be
\begin{equation}
\Delta_{12} = \pi + \frac{2\pi}{\lambda_1}\left[ \text{AD} - \frac{n_2}{n_1} \left(\text{AB} + \text{BC} \right) \right].\tag{47.38}
\end{equation}
We can replace the distances AB, BC, and AD in terms of the thickness \(d\) of the film, angle of incidence \(\theta\) and angle of refraction \(\theta_r\text{.}\)
\begin{align*}
\text{AB} \amp = \text{BC} = \frac{d}{\cos\theta_r}\\
\text{AD} \amp = \text{AC} \sin\theta = 2 d \tan\theta_r \sin\theta \\
\amp = 2d \frac{n_2}{n_1}\ \frac{\sin^2\theta_r}{\cos\theta_r},
\end{align*}
where I have made use of the Snell’s law for the refraction at A, \(n_1\sin\theta = n_2 \sin\theta_r\text{.}\) Substituting for AB, BC and AD in the expression for \(\Delta_{12}\) gives
\begin{equation}
\Delta_{12} = \pi + \frac{2\pi}{\lambda_2} \times 2d \cos\theta_r.\tag{47.39}
\end{equation}
The interference will be constructive if this is integer multiple of \(2\pi\) and destructive if odd multiple of \(\pi\text{.}\)
\begin{align}
\amp \text{Constructive: } \Delta_{12} = n\times 2\pi \ \ (n\ \text{ integer})\tag{47.40}\\
\amp \text{Destructive: } \Delta_{12} = n^\prime \pi\ \ (n^\prime\ \text{ odd})\tag{47.41}
\end{align}
We can send \(\pi\) on the other side, simplify, and replace \(n\) and \(n^\prime\) by appropriate \(m\) and \(m^\prime\text{.}\) Due to moving \(\pi\) to the right side, the choice of \(m\) is different than that of \(n\text{.}\)
\begin{align}
\amp \text{Constructive: } 2 d \cos\theta_r = m\frac{\lambda_2}{2} \ \ (m\ \text{ odd})\tag{47.42}\\
\amp \text{Destructive: } 2 d \cos\theta_r = m^\prime \lambda_2 \ \ (m^\prime\ \text{ integer})\tag{47.43}
\end{align}