Force and Torque on an Electric Dipole

Section 33.2 Force and Torque on an Electric Dipole

Subsection 33.2.1 An Electric Dipole in a Constant Electric Field

Consider an electric dipole placed in a region of constant electric field as shown in Figure 33.5. Forces on the two charges will be equal in magnitude but opposite in direction. That will make the net force on the dipole zero.

Figure 33.5. An electric dipole in a uniform electric field. (a) The forces on the two opposite charges of the dipole are equal in magnitude and opposite in direction. This results in the vanishing of the net force on the dipole. (b) and (c): The torque of the forces on the two charges have the same sense and therefore add to give a non-zero torque. The direction of the torque depends on the relative orientations of the dipole moment and the external electric field.

However, if the dipole is oriented at an angle to the electric field, then there will be a non-zero torque on the dipole since the forces on the two charges form a couple. Since the net force on the dipole is zero, the torque will be independent of the pivot point for the calculation of the torque with following result,

\begin{equation*} \vec \tau = \vec d\times q\vec E = q\vec d \times \vec E. \end{equation*}

Replacing \(q\vec d\) as the dipole moment vector \(\vec p\text{,}\) we see that the torque on the dipole is equal to the vector product of the dipole moment vector and the electric field vector \(\vec E\text{.}\)

\begin{equation} \vec \tau =\vec p \times \vec E.\tag{33.2} \end{equation}

Thus, when a polar molecule such as the water molecule is placed in an external electric field, the molecule experiences a torque that will cause the molecule to acquire angular acceleration. Since the torque direction flips when dipole rotates past the direction of the electric field, rotation speed will slow down, come to a stop, and reverse direction as shown in Figure 33.6. This will result in the oscillation of the direction of the dipole moment vector about the direction of the electric field. The damping of this motion leads to the dipole momet vector \(\vec p\) settling in the same direction as the electric field \(\vec E\text{.}\)

Subsection 33.2.2 (Calculus) Dipole in a Non-Uniform Electric Field

Electric force on a dipole is zero if the electric field is uniform since the oppositely directed forces on \(+q\) and \(-q\) of equal magnitude cancel each other exactly. However, if electric field is non-uniform, such as the electric field of a point charge, the two charges of the dipole will be in different electric fields, and hence the net force on the dipole will not be zero.

As in the figure, we will calculate net force in a simpler situation - assume direction of electric field is fixed in the positive \(y\) axis direction, but its magnitude varies with \(x\) coordinate of space.

\begin{equation*} \vec E = \hat j\, E_y(x). \end{equation*}

Denoting \(E_y(x=x_+)\) by \(E_{+,y}\) and \(E_y(x=x_-)\) by \(E_{-,y}\text{,}\) we write the \(y\) component of the net force to be

\begin{align*} F_y \amp = q E_{+,y} - q E_{-,y} = q \left( x_+ - x_- \right) \, \dfrac{ E_{+,y} - q E_{-,y}}{ x_+ - x_- }\\ \amp = q d\,\sin\theta \, \dfrac{ \Delta E_y}{ \Delta x }. \end{align*}

If the dipole is microscopic, we can take the small \(d\) limit, which would also be \(\Delta x \rightarrow 0\) limit. As \(\Delta x \rightarrow 0\text{,}\) \(\Delta E_y/\Delta x\) will be replaced by partial \(x\)-derivative of the electric field. Furthermore, \(q d\,\sin\theta\) is just \(p_x\) of the dipole moment vector \(\vec p\text{.}\) Therefore,

\begin{equation*} F_y = p_x \frac{\partial E_y}{\partial x}. \end{equation*}

For \(\vec p\) in an arbitrary direction, the partial derivative is replaced by nabla vector operator \(\vec \nabla\text{.}\) Thus, we replace \(p_x\,\partial/\partial_x\) by \(\vec p\cdot \vec\nabla\text{.}\)

\begin{equation*} \vec F = \left(\vec p\cdot \vec \nabla\right) \vec E, \end{equation*}

where

\begin{equation*} \vec \nabla = \hat i\, \dfrac{\partial }{\partial x} + \hat j\, \dfrac{\partial }{\partial y}+ \hat k\, \dfrac{\partial }{\partial z}, \end{equation*}

so that

\begin{equation} \vec F = \left(p_x\, \dfrac{\partial }{\partial x} + p_y\, \dfrac{\partial }{\partial y}+ p_z\, \dfrac{\partial }{\partial z}\right) \vec E.\tag{33.3} \end{equation}

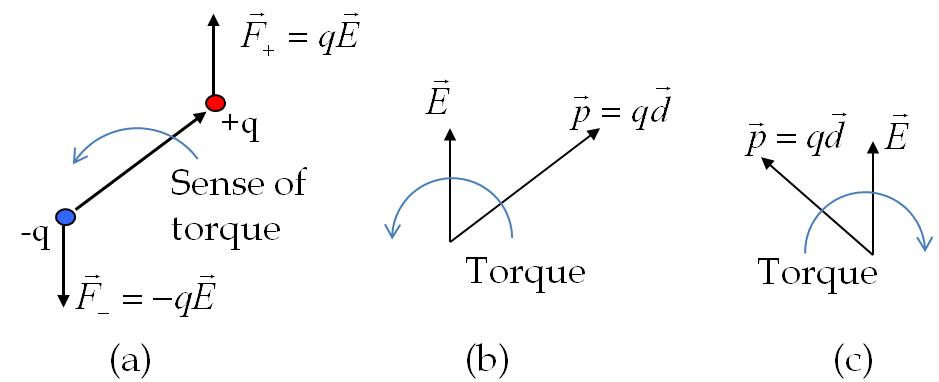
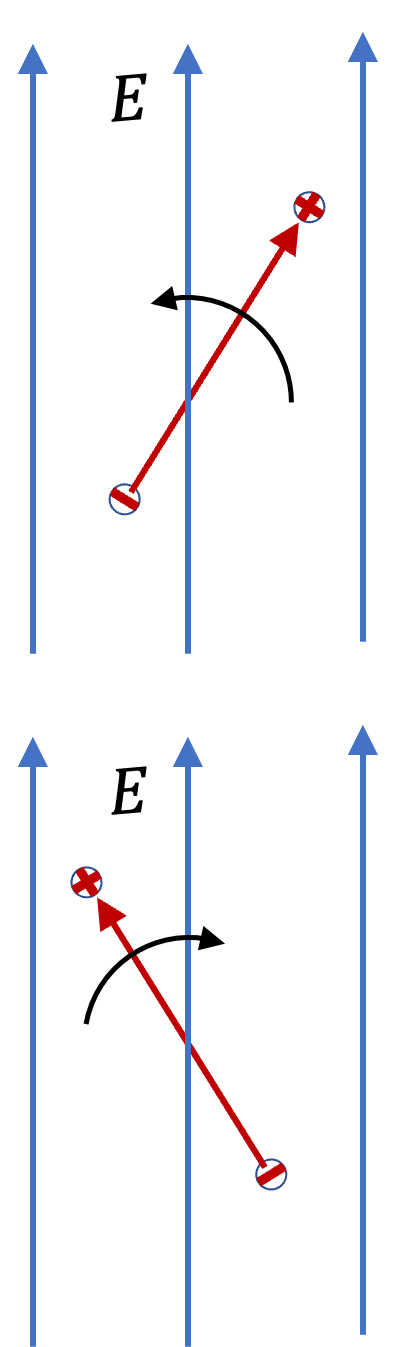
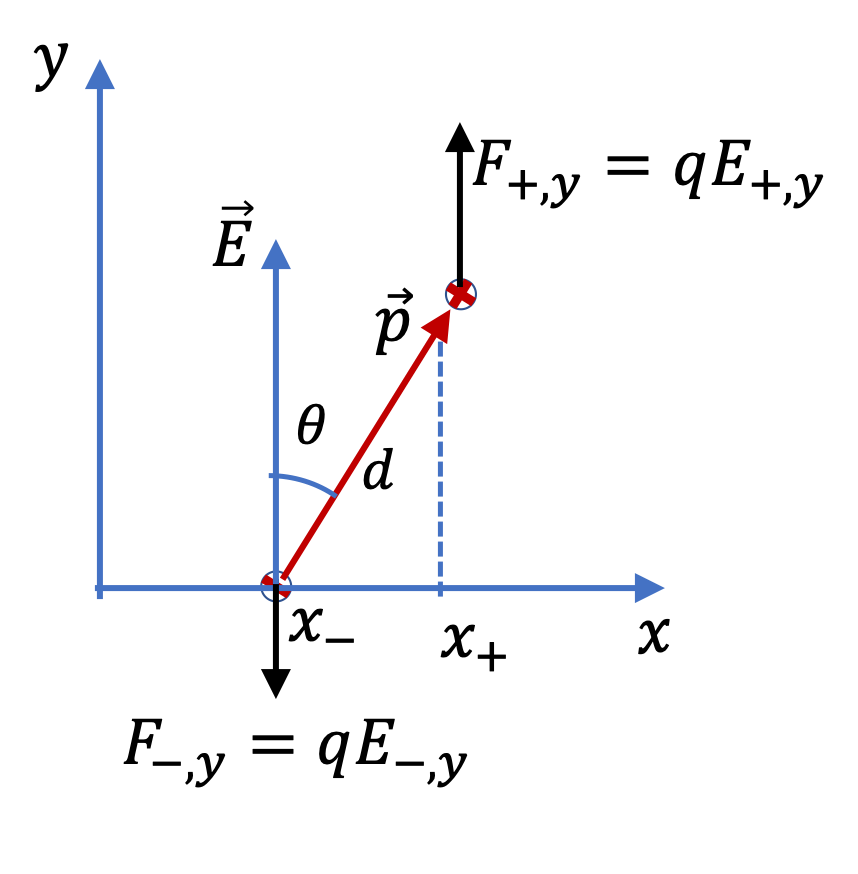
Example 33.7. (Calculus) Force and Torque on a Dipole in a Non-uniform Field.

A dipole has dipole moment of magnitude \(5 \times 10^{-12}\) Cm. The dipole is placed \(2.0\text{ mm}\) from a fixed \(3\, \mu\)C charge. Find the force and torque on the dipole (a) when the dipole is pointed away from the fixed charge, (b) when the dipole is pointed \(90^{\circ}\) from the fixed charge.

Hint: (a) Place the charge at the origin and the dipole along \(z\) axis. (b) Point the dipole towards \(x\) axis.

Answer.

(a) \(-34 \text{ N}\ \hat u_z \text{,}\) \(\tau=0\) (b) \(16.8\text{ N}\ \hat u_x\text{,}\) \(-3.38\times 10^{-2}\ \textrm{N.m}\ \hat u_y \text{.}\)

Solution 1. (a)

For concreteness, we place the fixed point charge at the origin, and the dipole be located along \(z\) axis with its direction towards positive \(z\) axis . The net force will have only \(z\)-component. We can get tha from taking derivative of the electric field.

\begin{align*} F_z \amp = p_z\frac{\partial}{\partial z}\left( \frac{1}{4\pi \epsilon_0}\frac{q}{r^2} \frac{z}{r}\right)_{r=z}\\ \amp = -\frac{qp}{2\pi \epsilon_0}\frac{1}{z^3} = - 34 \ \text{N}. \end{align*}

Therefore, the magnitude of the force is \(34 \ \text{N}\) and the direction is pointed towards negative \(z\) axis.

The torque will be zero since direction of the field is parallel to the direction of the electric field moment.

\begin{equation*} \vec \tau = \vec p \times \vec E = 0. \end{equation*}

Solution 2. (b)

Let \(x\) axis be the direction of the dipole moment while located on \(z\) axis. Now, we expect force from \(p_x\) and \(x\) derivative of electric field. Let us work with all components here since, we have mixed directions.

\begin{align*} \vec F \amp = p_x \frac{\partial}{\partial x} \left( \frac{1}{4\pi \epsilon_0}\frac{q}{r^2}\dfrac{x\hat u_x + y\hat u_y + z \hat u_z }{\sqrt{x^2+y^2+z^2}} \right)_{x=0, y=0, z=z} \\ \amp = p_x \frac{1}{4\pi \epsilon_0}\frac{q}{z^3}\hat u_x = 16.8\text{ N}\ \hat u_x. \end{align*}

Therefore, there is no net force on the dipole. It makes sense since for dipole to be pointed towards \(x\) axis, both charges are about the same distance from the charge at origin.

The torque will be

\begin{align*} \vec \tau \amp = \vec p \times \vec E = p\hat u_x \times E \hat u_z \\ \amp = -pE\hat u_y = -\frac{qp}{4\pi \epsilon_0}\frac{1}{z^2} \hat u_y= -3.38\times 10^{-2}\ \hat u_y\ \textrm{N.m}. \end{align*}

Example 33.8. (Calculus) Computing Force on a Dipole by a Point Charge.

Find the force on a dipole of dipole moment \(\vec p\) from a fixed charge \(q\) in each of the cases shown in the figure.

Answer.

(a) \(F_x = - \dfrac{pq}{2\pi\epsilon_0}\: \dfrac{1}{d^3}\text{,}\) (b) \(- \dfrac{pq}{4\pi\epsilon_0}\: \dfrac{1}{d^3} \text{.}\)

Solution 1. (a)

Let the point charge be at the origin and the line shown in the figure be \(x\) axis. Then the electric field from the point charge is pointed in the same direction as the dipole.

\begin{equation*} F_x = p\dfrac{\partial}{\partial x}\left( \dfrac{q}{4\pi\epsilon_0}\: \dfrac{1}{x^2}\right) = - \dfrac{pq}{2\pi\epsilon_0}\: \dfrac{1}{d^3}. \end{equation*}

The dipole is attracted towards increasing electric field.

Solution 2. (b)

Let the direction of the dipole be in the \(y \) axis direction. We need the rate at which the electric field by q is changing with y-coordinate and evaluate it at \(y = 0\text{.}\)

\begin{align*} \left.\dfrac{\partial \vec E}{\partial y}\right|_{y=0,z=0} \amp = \dfrac{q}{4\pi\epsilon_0}\: \dfrac{\partial }{\partial y} \left[ \frac{x\:\hat u_x + y\:\hat u_y + z\:\hat u_z}{\left(x^2 +y^2 +z^2 \right)^{3/2}} \right] \\ \amp = \dfrac{q}{4\pi\epsilon_0}\:\dfrac{1}{x^3}\:\hat u_y. \end{align*}

Therefore, the force is in the y-direction with y-component given by

\begin{equation*} F_y = - \dfrac{pq}{4\pi\epsilon_0}\: \dfrac{1}{d^3}. \end{equation*}

Exercises 33.2.3 Exercises

1. Torque on Electric Dipole of Water by External Electric Field.

The dipole moment of a water molecule between two large copper plates separated by a distance of \(5\, \text{mm}\) in the north-south direction is pointed due east. Find the torque on the molecule, when a voltage of \(150\, \text{V}\) is applied across the plates so that electric field is pointed due north. (Use only the permanent dipole moment of water molecule.)

Answer.

\(1.8\times 10^{-25}\, \text{N.m}\text{.}\)

Solution.

The angle between the dipole moment vector and the electric field is \(90^{\circ}|\text{.}\) Therefore, the magnitude of torque on the water molecule will be

\begin{align*} \tau \amp = p\:E\: \sin\theta = 6.1\times 10^{-30}\:\textrm{C.m}\times 150\:\dfrac{\textrm{V}}{\textrm{m}}\:\sin 90^{\circ}\\ \amp = 1.83\times 10^{-25}\:\textrm{N.m} \end{align*}

Prev Top Next