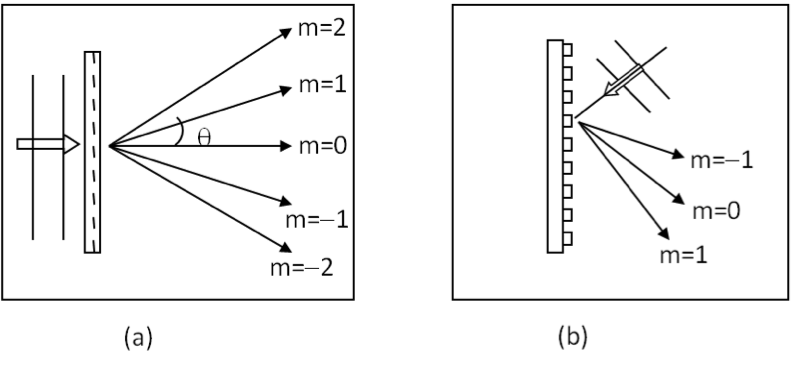
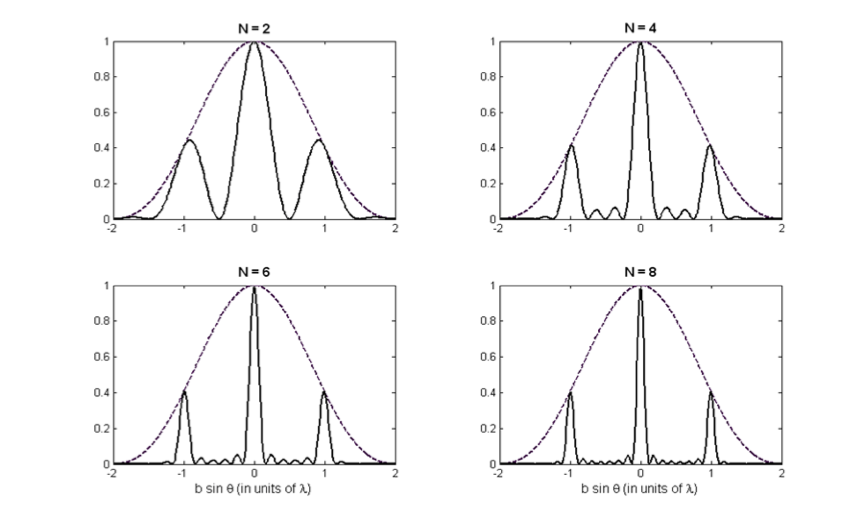
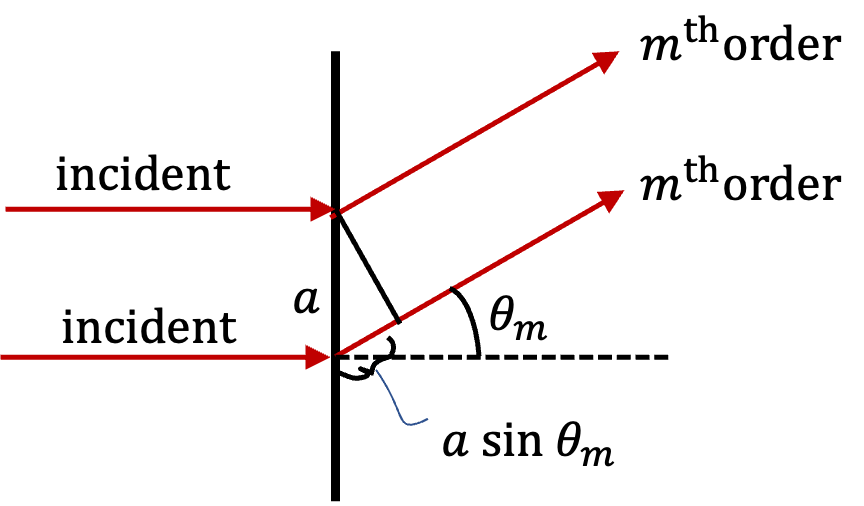
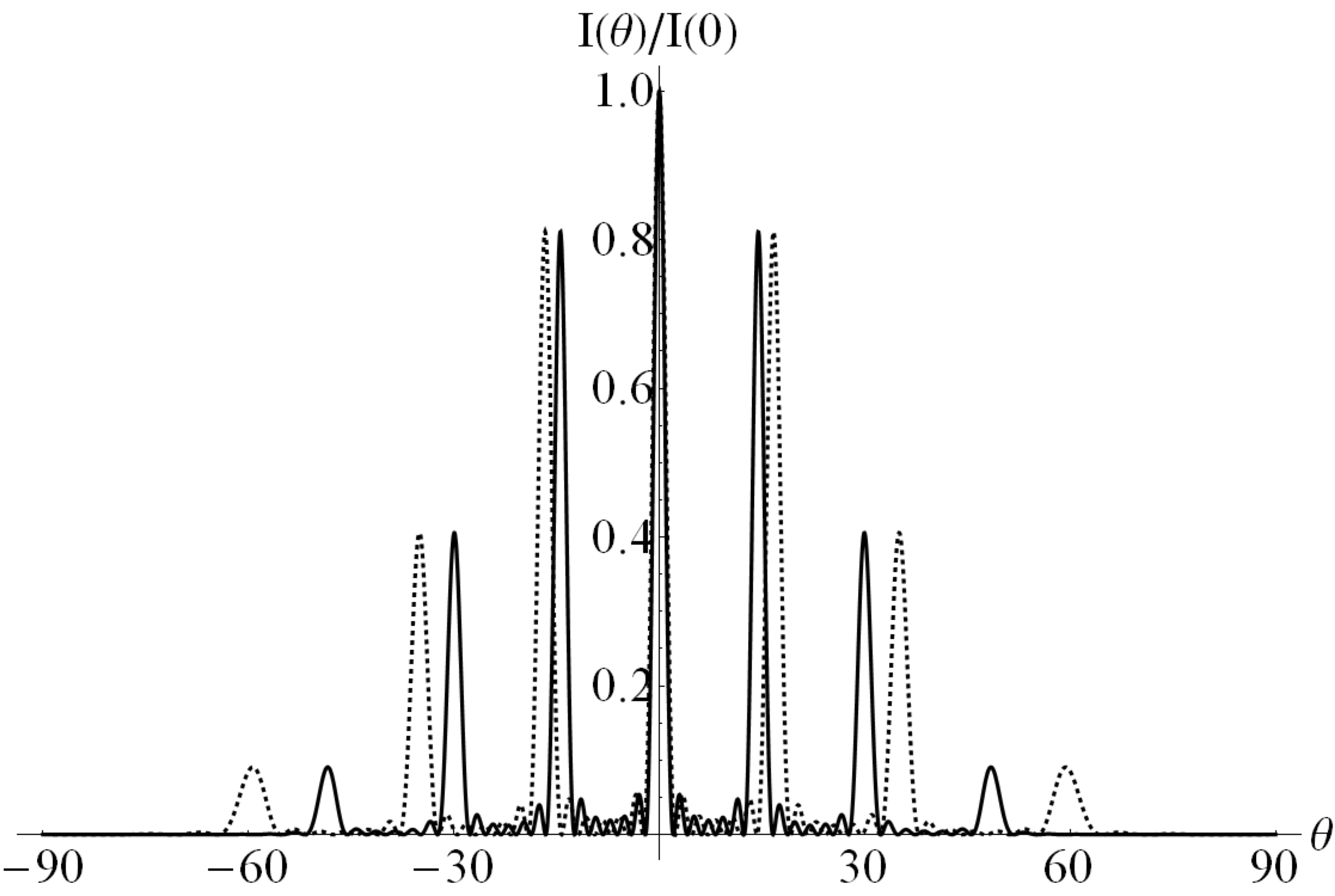
Example 48.33. Resolving the Sodium Doublet.
The D-line of sodium consists of two different wavelengths, \(589.0\, \text{nm}\) and \(589.6\, \text{nm}\text{.}\) A beam of light from a sodium lamp forms a beam of width \(10\, \text{mm}\text{.}\) The beam is incident perpendicularly on a diffraction grating that has \(8000\) rulings over a width of \(10\, \text{mm}\text{.}\) (a) Find the directions of the first-order principal peaks for the two wavelengths. (b) Decide if the two peaks resolvable in the first order. (c) Find the number of lines of a grating so that peaks in the first order are barely resolved?
Solution 1. a
We need separation \(a\) between the slits to figure out the direction of the first-order principal peak.
\begin{equation*}
a = \frac{10\ \textrm{mm}}{8000\ \textrm{lines}} = 1250\ \textrm{nm}.
\end{equation*}
For \(m = 1\text{,}\) the condition for the principal peak is \(a\sin\theta = \lambda\text{.}\) Let us denote the angle for the wavelength \(589.0\, \text{nm}\) by \(\theta\) and the angle for the wavelength \(589.6\, \text{nm}\) by \(\phi\text{.}\) Hence the directions of \(m = 1\) peaks for the the two wavelengths are
\begin{align*}
\amp \theta_1 = \sin^{-1}\left( \frac{589.00\ \textrm{nm}}{1250\ \textrm{nm}} \right) = 0.49065\ \textrm{rad}\\
\amp \phi_1 = \sin^{-1}\left( \frac{589.59\ \textrm{nm}}{1250\ \textrm{nm}} \right) = 0.49119\ \textrm{rad}
\end{align*}
Solution 2. b
We can compare the resolution required to the resolving power of the grating to see if the peaks will be resolved. The resolving power required for resolving the the two given wavelengths is
\begin{equation*}
R_{\textrm{req}} = \frac{\lambda_{\textrm{ave}}}{\Delta \lambda} = \frac{589.295\ \textrm{nm}}{0.59\ \textrm{nm}} = 999.
\end{equation*}
The resolving power of the given grating for \(m=1\) peaks is
\begin{equation*}
R_{\textrm{grating}} = Nm = 8000.
\end{equation*}
Since \(R_{\textrm{grating}} > R_{\textrm{req}}\) the peaks will be resolved.
Solution 3. c
Using the required resolving power, we can work backwards and deduce the number of lines required in 10 mm, the beam width, so that the grating can resolve the two given waves.
\begin{equation*}
Nm = R_{\textrm{req}} \ \ \Longrightarrow\ \ N \times 1 = 999 \ \ \Longrightarrow\ \ N= 999.
\end{equation*}