Working with Cartesian Unit Vectors

Section 3.7 Working with Cartesian Unit Vectors

Unit Vectors Along Cartesian Positive Axis Directions.

Unit vectors along Cartesian axes play important role in vector analysis. We will often denote these unit vectors by \(\hat u_x \text{,}\) \(\hat u_y \text{,}\) and \(\hat u_z \) respectively. At other times, we will denote them by their traditional symbols \(\hat i \text{,}\) \(\hat j \text{,}\) and \(\hat k \) respectively.

For instance, say, we want a position vector \(\vec r = ( x=2 \text{ m}, y=-5 \text{ m}) \) in the \(xy\)-plane. Then, you can see that this vector will be a sum of two vectors: \(\vec r_1 = 2 \text{ m} \hat i \) and \(\vec r_2 = -5 \text{ m} \hat j \text{.}\) We write this as

\begin{equation*} \vec r = 2 \text{ m} \hat i - 5 \text{ m} \hat j. \end{equation*}

In general, an arbitrary vector \(\vec A \) with coordinate components \(A_x, A_y, A_z\) is often written as a sum of vectors along the Cartesian axes.

\begin{equation*} \vec A = A_x \hat i + A_y \hat j + A_z \hat k. \end{equation*}

Subsection 3.7.1 Dot and Cross Products of Cartesian Unit Vectors

Since \(\hat i\text{,}\) \(\hat j\text{,}\) and \(\hat k\text{,}\) has unit magnitude, and are perpendicular to each other, we get the following dot and cross products.

\begin{align} \text{Dot products: }\amp\hat i \cdot \hat i = 1,\ \ \hat j \cdot \hat j = 1,\ \ \hat k \cdot \hat k = 1,\tag{3.30}\\ \amp \hat i \cdot \hat j = 0,\ \ \hat j \cdot \hat k = 0,\ \ \hat k \cdot \hat i = 0,\tag{3.31}\\ \text{Cross products: }\amp\hat i \times \hat i = 0,\ \ \hat j \times \hat j = 0,\ \ \hat k \times \hat k = 0,\tag{3.32}\\ \amp \hat i \times \hat j = \hat k,\ \ \hat j \times \hat k = \hat i,\ \ \hat k \times \hat k = \hat j,\tag{3.33} \end{align}

To Student: Prove these results using the definitions of scalar and vector product. The magnitudes of these vectors are all 1 and they are mutually perpendicular to each other.

With these, you can easily see how the components of an arbitrary vector \(\vec A = \left( A_x, A_y, A_z\right)\) are just the dot product of \(\vec A \) with the unit vectors along the axex.

\begin{equation*} A_x = \vec A \cdot \hat i,\ \ A_y = \vec A \cdot \hat j,\ \ A_z = \vec A \cdot \hat k. \end{equation*}

The magnitude of \(\vec A \) is same as before

\begin{equation*} A = \sqrt{\vec A \cdot \vec A} = \sqrt{A_x^2 + A_y^2 + A_z^2}. \end{equation*}

Cosines of the angles \(\vec A\) makes with positive axes, called direction cosines of the vector, are

\begin{equation*} \cos\,\theta_x = \dfrac{A_x}{A},\ \ \cos\,\theta_y = \dfrac{A_y}{A},\ \ \cos\,\theta_z = \dfrac{A_z}{A}, \end{equation*}

of which you only need two to denote direction of \(\vec A\) since

\begin{equation*} \cos^2\theta_x + \cos^2\theta_y + \cos^2\theta_z = 1. \end{equation*}

Figure 3.96. Angles for direction cosines.

Proof: It is easy to prove relation between direction cosines.

\begin{align*} \cos^2\theta_x \amp + \cos^2\theta_y + \cos^2\theta_z \\ \amp = \left( \frac{A_x}{A} \right)^2 + \left( \frac{A_y}{A} \right)^2 + \left( \frac{A_z}{A} \right)^2 \\ \amp = \frac{A_x^2 + A_y^2 + A_z^2}{A^2} = \frac{A^2}{A^2} = 1. \end{align*}

Subsubsection 3.7.1.1 Dot Product of Two Vectors Using Cartesian Unit Vectors

A dot product of two vectors is rather simple to obtain from their Cartesian components. Let

\begin{equation*} \vec A = A_x \hat i + A_y \hat j + A_z \hat k,\ \ \vec B = B_x \hat i + B_y \hat j + B_z \hat k. \end{equation*}

Then, we will have

\begin{align*} \vec A \cdot \vec B \amp = (A_x \hat i + A_y \hat j + A_z \hat k) \cdot (B_x \hat i + B_y \hat j + B_z \hat k)\\ \amp = A_x B_x (\hat i \cdot \hat i) + A_x B_y (\hat i \cdot \hat j) + A_x B_z (\hat i \cdot + \hat k) + \cdots\\ \amp = A_x B_x (1) + A_x B_y (0) + A_x B_z (0) + \cdots\\ \amp = A_x B_x + A_y B_y + A_z B_z. \end{align*}

Of course this will equal \(A B \cos\theta\) with angle \(\theta\) between the two vectors.

\begin{equation} \vec A \cdot \vec B = A B \cos\theta = A_x B_x + A_y B_y + A_z B_z.\tag{3.34} \end{equation}

Subsubsection 3.7.1.2 Cross Product of Two Vectors Using Cartesian Unit Vectors

I have already given formulas for this above.

\begin{equation*} \vec A \times \vec B = \left(A_y B_z - A_z B_y\right) \hat i + \left(A_z B_x - A_x B_z\right) \hat j + \left(A_x B_y - A_y B_x\right) \hat k. \end{equation*}

\begin{align*} \vec A \times \vec B \amp = (A_x \hat i + A_y \hat j + A_z \hat k) \times (B_x \hat i + B_y \hat j + B_z \hat k) \\ \amp = A_x B_x (\hat i \times \hat i) + A_x B_y (\hat i \times \hat j) + A_x B_z (\hat i \times + \hat k) + \cdots\\ \amp = A_x B_x (0) + A_x B_y (\hat k) + A_x B_z (- \hat j) + \cdots\\ \amp = [A_x B_y (\hat k) + A_x B_z (- \hat j)] + [A_y B_x (-\hat k) + A_y B_z (\hat i)] \\ \amp \ \ \ \ \ \ + [A_z B_x (\hat j) + A_z B_y (-\hat i)] \\ \amp = \left(A_y B_z - A_z B_y\right) \hat i + \left(A_z B_x - A_x B_z\right) \hat j + \left(A_x B_y - A_y B_x\right) \hat k. \end{align*}

Often, we express this result in the form of a determinant.

\begin{equation} \vec A \times \vec B = \begin{vmatrix} \hat i \amp \hat j \amp \hat k \\ A_x \amp A_y \amp A_z \\ B_x \amp B_y \amp B_z \\ \end{vmatrix} \tag{3.35} \end{equation}

Exercises 3.7.2 Exercises

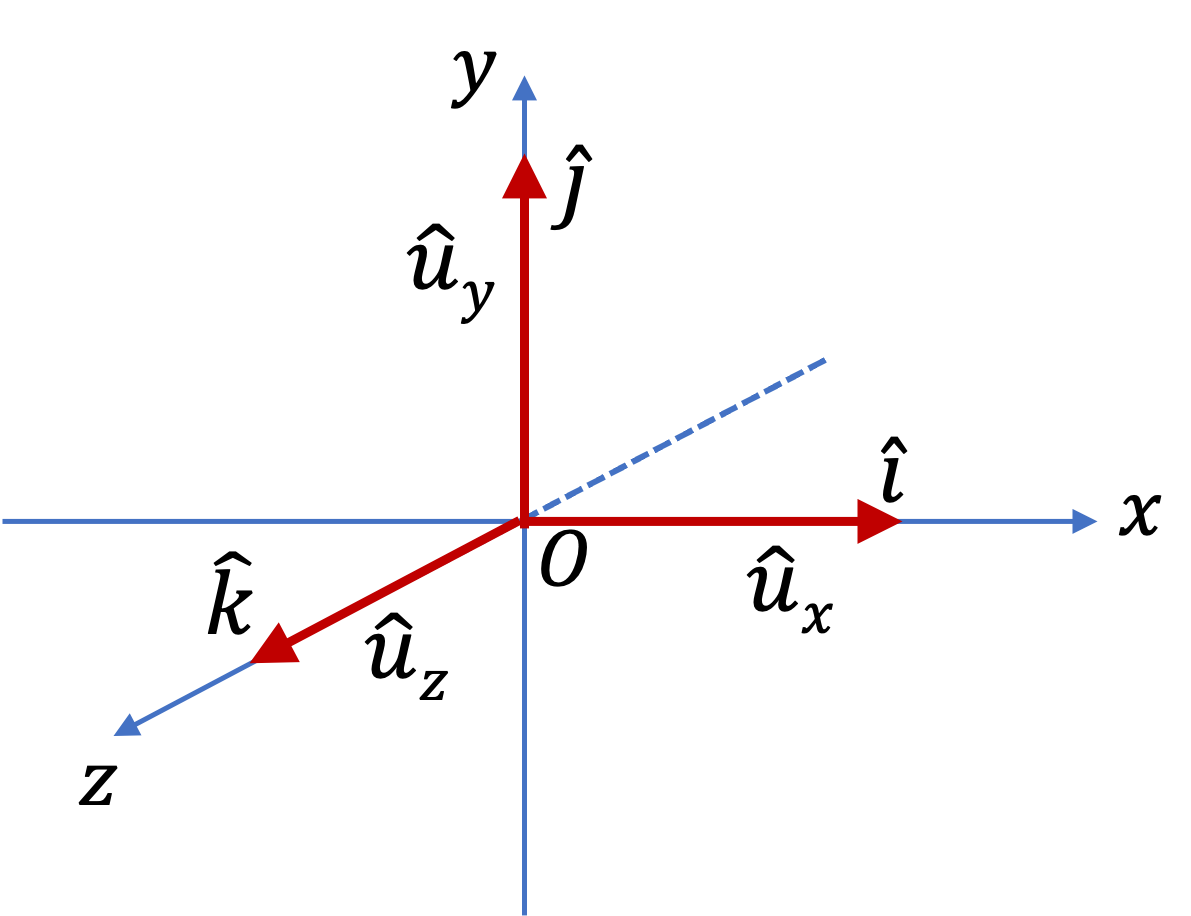
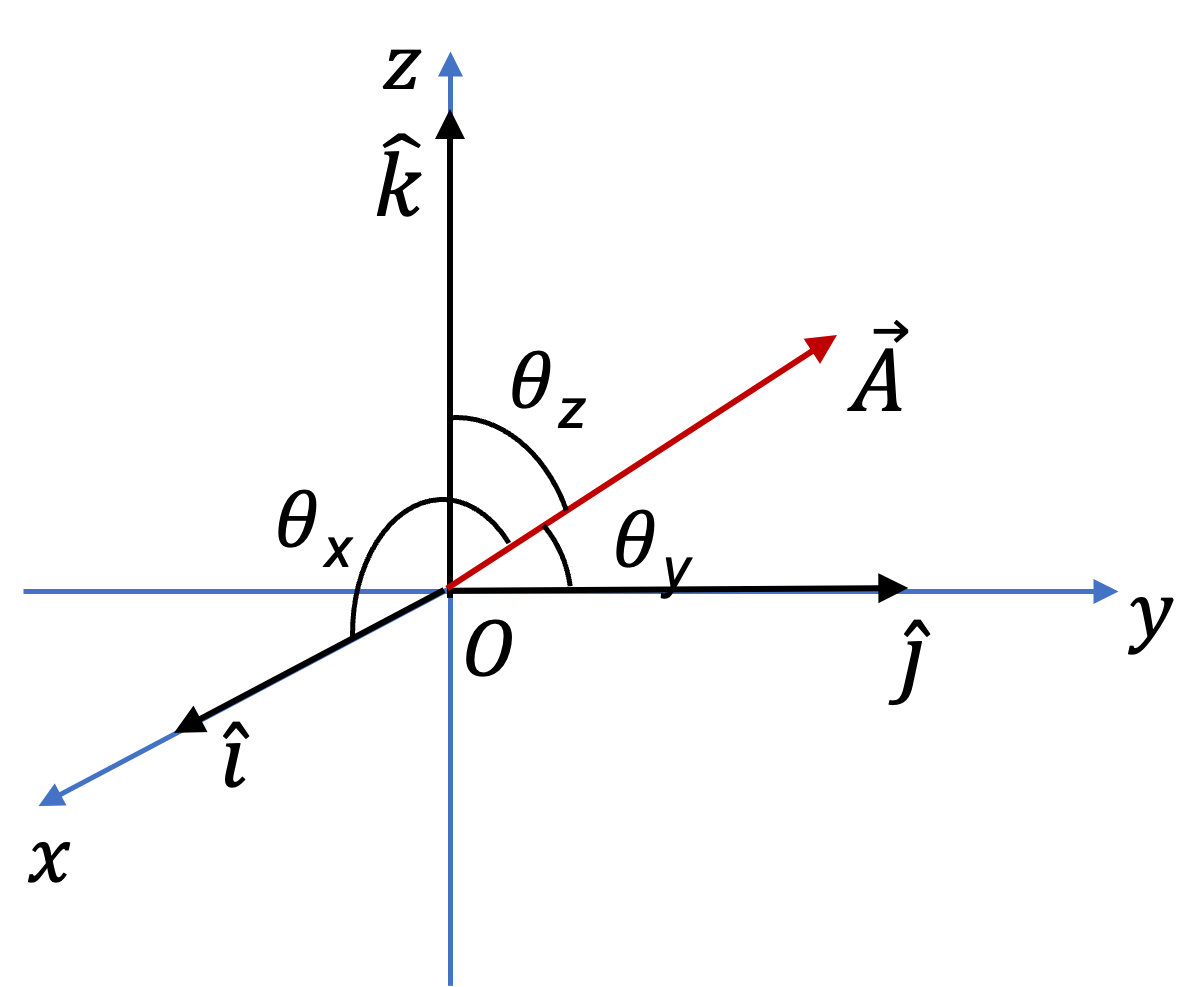
1. Practice with Dot Product of Unit Vectors.

Using \(\vec A = A_x \hat i + A_y \hat j + A_z \hat k\text{,}\) prove that \(\vec A \cdot \vec A = A_x^2 + A_y^2 + A_z^2\text{.}\)

Hint.

Expand

Answer.

N/A

Solution.

We display the calculation for \(x \) in detail and infer those for \(y \) and \(z \) from the symmetry.

\begin{align*} \vec A \cdot \vec A \amp =(A_x \hat i + A_y \hat j + A_z \hat k)\cdot (A_x \hat i + A_y \hat j + A_z \hat k) \\ \amp = A_x \left( A_x \hat i\cdot \hat i + A_y \hat i \cdot \hat j + A_z \hat i \cdot \hat k \right) + (x \rightarrow y) + (x \rightarrow z) \\ \amp = A_x \left( A_x \times 1 + A_y \times 0 + A_z \times 0 \right) + (x \rightarrow y) + (x \rightarrow z) \\ \amp = A_x^2 + (x \rightarrow y) + (x \rightarrow z) \\ \amp = A_x^2 + A_y^2 + A_z^2. \end{align*}

2. Practice with Friends: Algebraic Manipulation of Vectors Given as Components.

Consider two vectors expressed in terms of Cartesian unit vectors.

\begin{equation*} \vec A = 3\hat i + 4\hat j - 12 \hat k,\ \ \vec A = -3\hat i + 4\hat j + 12 \hat k \end{equation*}

Find (a) magnitudes \(A\) and \(B\text{,}\) (b) sum \(\vec A + \vec B\text{,}\) (c) difference \(\vec A - \vec B\text{,}\) (d) dot product \(\vec A \cdot \vec B\text{,}\) (e) cross product \(\vec A \times \vec B\text{,}\) (f) angle between the two vectors, and (g) direction cosines of \(\vec A\text{.}\)

Answer.

(a) \(13 \text{,}\) \(13\text{,}\) (b) \(8 \hat j \text{,}\) (c) \(6 \hat i -24 \hat k \text{,}\) (d) \(-137 \text{,}\) (e) \(96 \hat i + 24 \hat k \text{,}\) (f) \(\cos^{-1}(-137/169)\text{,}\) (g) \(\cos^{-1}(3/13)\)

Prev Top Next