The Basics
1. Angular Magnification of a Convex Lens.
Follow the link: Exercise 45.1.5.1.
2. Angular Magnification for Convex Lens if Eye Very Close.
Follow the link: Exercise 45.1.5.2.
Section 45.8 Optical Instruments Bootcamp
Exercises Exercises
The Human Eye
3. Power of a Typical Human Eye.
Follow the link: Exercise 45.2.5.1.
4. Image Formed by a Far-Signted Person.
Follow the link: Example 45.10.
5. Image of an Object Placed at the Near Point.
Follow the link: Exercise 45.2.5.2.
6. Power of the Corrective Lens for a Near-sighted Eye.
Follow the link: Exercise 45.2.5.3.
7. Power of the Corrective Lens for a Far-sighted Eye.
Follow the link: Exercise 45.2.5.4.
8. Corrective Lens for a Near-Sighted Person.
Follow the link: Exercise 45.2.5.5.
The Magnifying Glass
9. AAngular Magnification of a Magnifying Glass.
Follow the link: Exercise 45.3.2.1.
10. Angular Magnification by a Magnifying Glass for a Typical Eye.
Follow the link: Exercise 45.3.2.2.
11. Power of Magnifying Glass from Observed Magnification.
Follow the link: Exercise 45.3.2.3.
Microscope
12. Perceived Size of a Microscopic Specimen in a Compound Microscope.
Follow the link: Exercise 45.4.2.1.
13. Thickness of Hair from Magnification and Apparent Thickness.
Follow the link: Exercise 45.4.2.2.
Pin-Hole Calmera
14. Image and Angular Magnification of a Pin-hole Camera.
Follow the link: Example 45.18.
Telescope
15. Magnification of a Telescope from Powers of the Objective and the Eyepiece.
Follow the link: Example 45.29.
16. Magnification of Galileo’s First Telescope.
Follow the link: Exercise 45.6.4.1.
17. Magnifying Power and F/# of a Reflecting Telescope.
Follow the link: Example 45.30.
18. Diameter of a Planet from Angle Subtended and Magnification.
Follow the link: Exercise 45.6.4.2.
19. Diameter of Airy Disk of a Star on a CCD Camera.
Follow the link: Exercise 45.6.4.3.
Miscellaneous
20. Angular Size of the Image of the Moon.
What is the angular size of the Moon if viewed from a binocular that has a focal length of \(1.2\text{ cm}\) for the eyepiece and a focal length of \(8\text{ cm}\) for the objective? Use the radius of the Moon to be \(1.74 \times 10^6\text{ m}\) and the distance of the Moon from the observer to be \(3.8 \times 10^8\text{ m}\text{.}\)
Hint.
Use the angle subtended by the moon itself and magnification of the binucular.
Answer.
\(6.1\times 10^{-2}\text{ rad} \text{.}\)
Solution.
We use \(s=R\theta\) with \(s=\text{diameter of moon}\) and \(R=\text{distance to the Moon}\) to find the angle subtended by the Moon directly to be
\begin{equation*}
\theta = \frac{s}{R} = \frac{2\times 1.74 \times 10^6\text{ m}}{3.8 \times 10^8\text{ m}} = 9.158\times 10^{-3}\text{ rad}.
\end{equation*}
Multiplying by the magnification we will get the desired angle. So, we need the value for magnification. From the focal lengths of the objective and the eyepiece, we get the magnification of the binocular to be
\begin{equation*}
M = -\frac{f_\text{o}}{f_\text{e}} = -\frac{8\text{ cm}}{1.2\text{ cm}} = -6.67.
\end{equation*}
Therefore, the angle subtended by the image will me \(|M|\) times
\begin{equation*}
\theta_\text{image} = 6.67\times 9.158\times 10^{-3}\text{ rad} = 6.1\times 10^{-2}\text{ rad}.
\end{equation*}
21. Apparent Height of a Tree in a Telescope.
In a reflecting telescope the objective is a concave mirror of radius of curvature equal to \(50\text{ cm}\) and an eyepiece is a convex lens of focal length \(5\text{cm}\text{.}\) Find the apparent size of a \(25\text{-m}\) tree at a distance of \(10\text{ km}\) that you would perceive when looking through the telescope.
Hint.
The apparent height will be multiple of the magnification.
Answer.
\(125\text{ m}\)
Solution.
We have the following angular magnification of the telescope.
\begin{equation*}
M = -\dfrac{f_o}{f_e} = -\dfrac{50\:\textrm{cm}/2}{5\:\textrm{cm}} = - 5.
\end{equation*}
We can think of \(10\text{ km}\) as infinitely far away with virtual image forming that far as well, as is the case in telescopes. This happens in telescopes since the distance between objective and eyepiece is very close to the sum of their foci. Therefore, the height of the tree will be magnified \(5\) fold. That is the apparent height will be \(125\text{ m}\text{.}\)
22. Apparent Size of a Tree Through a Telescope.
In a reflecting telescope the objective is a concave mirror of radius of curvature \(2\,\text{m}\) and an eyepiece is a convex lens of focal length \(5\, \text{cm}\text{.}\) Find the apparent size of a \(25\, \text{m}\) tall tree at a distance of \(10\,\text{km}\) that you would perceive when looking through the telescope.
Solution.
We have the following angular magnification of the telescope.
\begin{equation*}
M = -\dfrac{f_o}{f_e} = -\dfrac{100\:\textrm{cm}}{5\:\textrm{cm}} = 20.
\end{equation*}
Let \(\theta\) be the angle subtended by the object and \(\theta'\) the angle subtended by the image.
\begin{equation*}
\theta' = M\:\theta \approx M\:\tan(\theta) = -20\times \dfrac{25\:\textrm{m}}{10\:\textrm{km}} = 0.05\:\textrm{rad}.
\end{equation*}
Since the image is formed at the near point which can be taken to be \(25\, \text{cm}\) from the eye we will find the following apparent height for the image.
\begin{equation*}
h_i = (25\:\textrm{cm})\:\tan(\theta') = 1.25\:\textrm{cm}.
\end{equation*}
23. Distance to the Stars from Separation Angle and Separation Distance.
Two stars that are \(10^9\,\text{km}\) apart are viewed by a telescope and found to be separated by an angle of \(10^{-5}\) radian. If the eyepiece of the telescope has a focal length of \(1.5\, \text{cm}\) and the objective has a focal length of \(3\,\text{m}\text{,}\) how far away are the stars from the observer?
Answer.
\(2 \times 10^{16}\, \text{km}\text{.}\)
Solution.
Let \(\theta\) be the angle subtended by the object and \(\theta'\) the angle subtended by the image. Then the magnification of telescope says that
\begin{equation*}
\left| \dfrac{\theta'}{\theta}\right| = |M| = \dfrac{f_o}{f_e}.
\end{equation*}
This gives
\begin{equation*}
|\theta| = \dfrac{f_e}{f_o}\times theta'.\ \ \ (1)
\end{equation*}
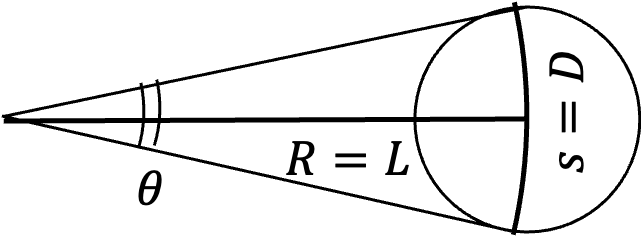
Suppose \(D\) be the distance between the stars and \(R\) the distance to the star, then
\begin{equation*}
\theta \approx \dfrac{D}{R}.\ \ \ (2)
\end{equation*}
From (1) and (2) we find
\begin{equation*}
R = \dfrac{D}{\theta} = \dfrac{f_o}{f_e\:\theta'}\times D.
\end{equation*}
Now, putting in the numerical values we get
\begin{equation*}
R = \dfrac{300\:\textrm{cm}}{ 1.5\:\textrm{cm}\times 10^{-5}\: \textrm{rad}}\times 10^9\: \textrm{km} = 2\times 10^{16}\: \textrm{km}
\end{equation*}
24. Angular Size of Moon when Viewed Through a Binucular.
What is the angular size of the Moon if viewed from a binocular that has a focal length of \(1.2\, \text{cm}\) for the eyepiece and a focal length of \(8\, \text{cm}\) for the objective? Use the radius of the Moon \(1.74 \times 10^6\,\text{m}\) and the distance of the Moon from the observer to be \(3.8 \times 10^8\,\text{m}\text{.}\)
Hint.
Use the angular magnification of the telescope.
Answer.
\(1.75^{\circ}\text{.}\)
25. Size of a Planet Using Angle Subtended.
An unknown planet at a distance of \(10^{12}\, \text{m}\) from the Earth is observed by a telescope that has a focal length of the eyepiece of \(1\, \text{cm}\) and a focal length of the objective of \(1\, \text{m}\text{.}\) If the far away planet is seen to subtend an angle of \(10^{-5}\) radian at the eyepiece, what is the size of the planet?
Solution.
The telescope has angular magnification \(M = - 100\text{.}\) Therefore, the angle subtended by the object will be \(|\theta| = \theta'/M = 10^{-5}\: \textrm{rad}/100 = 10^{-7}\: \textrm{rad}\text{.}\) Since the planet is \(10^{12}\, \text{m}\) away, the diameter of the planet will be \(D = R\, \theta = 10^{5}\, \text{m}\text{.}\)
