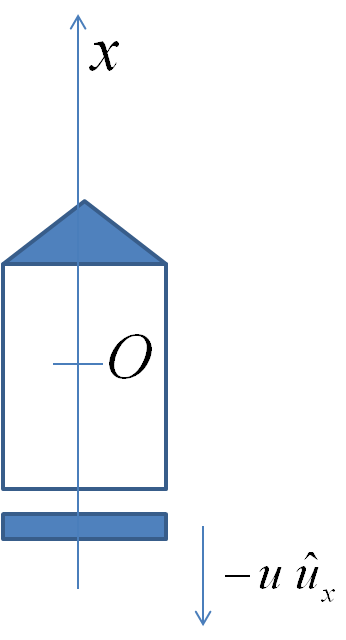
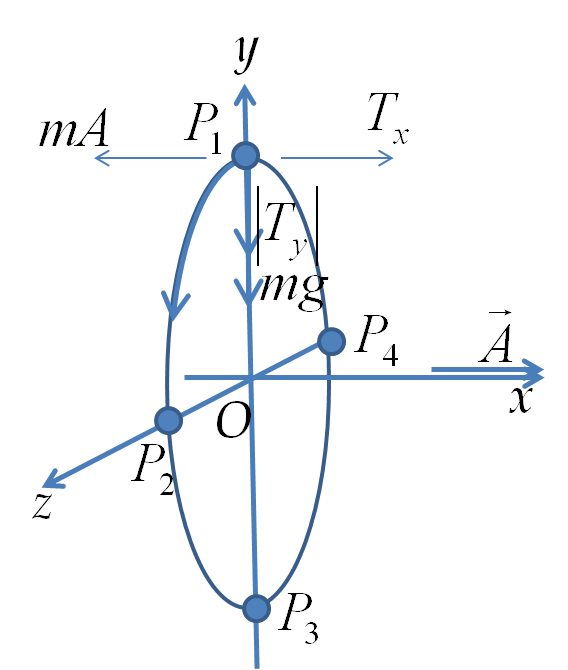
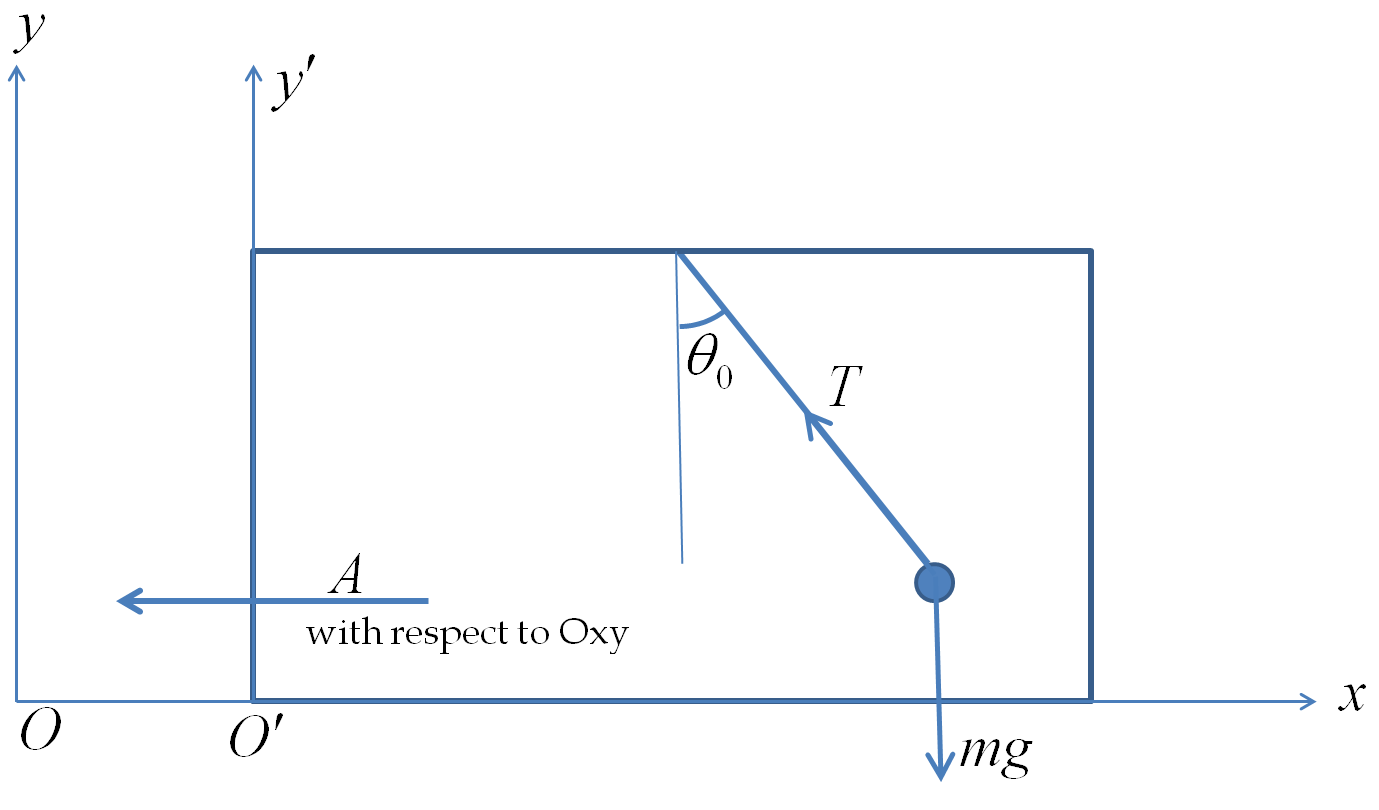
(b) Let the direction of the bob from the suspension point at some instant \(t\) be \(\theta\text{.}\) We will take \(\theta>\theta_0\) for concreteness in the calculations. The equations of motion in the non-inertial frame will now be
\begin{align*}
\amp x\text{-component: }\ \ -T\sin\theta +m A = m\frac{d^2x'}{dt^2}.\\
\amp y\text{-component: }\ \ T\cos\theta - m g = m\frac{d^2y'}{dt^2}.
\end{align*}
Although these equations are OK to work with but a better set will be the radial and angular coordinates of the bob with the origin at the suspension point rather that where it is shown in the figure. With this choice the angular equation of motion is written more readily as torque equation.
\begin{equation}
-mg L \sin\theta = mL^2 \frac{d^2 \theta}{dt^2}.\tag{11.19}
\end{equation}
Since \(\theta=\theta_0\) is the equilibrium angle, we define an angle \(\psi\) with respect to the equilibrium angle as
\begin{equation*}
\psi = \theta - \theta_0.
\end{equation*}
This gives the following for the small angle approximation for \(\psi\text{.}\)
\begin{equation*}
\sin\theta = \sin(\theta_0+\psi) = \sin\theta_0\cos\psi + \cos\theta_0\sin\psi \approx\sin\theta_0+ (\cos\theta_0)\psi,
\end{equation*}
Making the substitution in Eq.
(11.19) we obtain
\begin{align*}
\frac{d^2 \psi}{dt^2} \amp = -\left(\frac{g}{L}\cos\theta_0 \right) \psi - \frac{g}{L}\sin\theta_0\\
\amp = -\left(\frac{g}{L}\cos\theta_0 \right)\left( \psi - \frac{A}{g}\right)
\end{align*}
Let us define a displaced angle by
\begin{equation*}
\beta = \psi - \frac{A}{g}.
\end{equation*}
In terms of \(\beta\) the equation of motion becomes
\begin{equation*}
\frac{d^2 \beta}{dt^2} = -\left(\frac{g}{L}\cos\theta_0 \right) \beta \equiv - \omega^2 \beta.
\end{equation*}
Therefore, the frequency of small oscillations about the equilibrium will be
\begin{equation*}
f = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{g}{L}\cos\theta_0}.
\end{equation*}