States of Matter

Section 22.2 States of Matter

Subsection 22.2.1 Phases of Matter

A material can exit in different phases distinguishable by some physical property such as density. For instance, water can exist in solid, liquid and gas forms, which can be distinguished by the value of density, besides just the look. When water exists simultaneously in two or all three of these phases, they separate into different regions, some parts exist in one phase and other parts in other phases.

The density-based phases are not the only types of phases of interest to physicists. For instance, to us ice may all look the same, but there are at lease eight different types of ice, which are distinguishable by their crystal structure. They are different phases of ice. Many materials exist in more than one solid phase. The solid phases usually differ from each other in crystal structures and other physical properties.

Magnetic materials and dielectric materials also exhibits phases with different regions of the sample organized with different magnetic or electric properties.

To be specific, here, we will focus on phases distinguishable by density, e.g. the case of solid ice, liquid water, and water vapor, although our discussions can be applied to other types of phases as well.

Subsection 22.2.2 Phases Diagram

Phase diagram:

To display the equilibrium conditions under which a substance can exist in the solid, liquid, gas phases, or a mixture of phases, we ususally use the temperature-pressure (\((T,p)\)) plane and to see the phase change we use a \(\rho\) versus \(T\) or \(\rho\) versus \(p\) plot. Each point on the (\((T,p)\)) plane plane corresponds to an equilibrium state of the material as shown in Figure 22.3. The resulting picture is called a phase diagram of the material.

Regions and Coexistence Lines on a Phase Diagram

You can see in Figure 22.3 that most of the points in the phase diagram correspond to equilibrium conditions in which the material exists in only one phase. The entire region of conditions labeled solid corresponds to the equilibrium conditions under which the entire sample is in solid phase. Similarly, for the regions labeled liquid and gas.

The curves separating the pure phase regions are called coexistence lines. For instance, the line OA separates the regions of solids and gas. If you create the condition of a point on this line, then the material will exist in both solid and gas phase. By increasing or decreasing the energy of the system you can change the proportion of each phase in the material from 100% solid to 100% gas without any liquid present.

For instance, if you start to a little left of the curve OA the sample will be completely in the solid phase. As you increase the temperature of the system while keeping the pressure constant, you will reach the OA line. At the OA line, the solid will be sublimated to the gas without melting. Once all the solid has been transformed into gas phase more energy will increase the temperature of the gas and you will enter the pure gas phase region of the phase diagram.

Similarly, the equilibrium curve AC between liquid and gas phases denote the boiling and condensation points, and the equilibrium curve AB between solid and liquid phases correspond to melting and freezing points. The three curves, the sublimation curve OA, the melting curve AB and the evaporation curve AC meet at a point called the triple point where all three phases coexist in equilibrium. Triple points of several substances, such as hydrogen (13.80 K, 7.04 kPa), neon (24.56 K, 43.2 kPa), nitrogen (63.18 K, 12.5 kPa) and water (273.16 K, 0.610 kPa) are used for the calibration of Thermometer.

Critical Point:

The equilibrium curve between the liquid and gas phases terminates at the critical point beyond which the separated identities of liquid and gas phases disappear. For instance, if you start with state D which is all in liquid phase and change pressure and temperature along the dotted curve shown in Figure 22.3, the material will undergo a phase transformation from all liquid at D to all gas phase at E without any phase separation; there would be no point at which you would have two separate densities in the sample.

Critical pressures and temperatures are well above normal temperatures for most common substances. For instance critical point of water/steam system is (647.4 K, 22,120 kPa). Consequenctly, we do not encounter strange behavior associated with the critical point in everyday life. However, conditions above critical points are commonly used in industrial applications, e.g., the boilers of electric generating plants reach well above the critical point of steam.

Suppose you place some ice in a enclosed container with a movable piston so that pressure inside the container remains constant. We will conduct an experiment of heating the sample at constant pressure and monitoring its thermodynamic state, meaning its \((T,\ p,\ \rho)\) values. The line S-SL-L-LG-G in Figure 22.3 shows such a process.

As you heat ice at point S, its temperature will increase, giving us ice at different states, meaning ice at different values of \((T,\ p,\ \rho)\text{.}\) Once ice has melted at SL interphase, the heating of liquid water will also take water through various thermodynamic states of the liquid phase.

Eventually, we will come to the point LG where liquid water starts to boil and you will find both liquid water and water vapor in equilibrium. Once the entire water sample has been converted into vapor, more heating takes the vapor through various thermodynamic states of the gas phase.

Subsection 22.2.3 Heat of Transformation

Put some ice and water in a metal container so that you have an ice and water mixture at the end. Place a Thermometer in the container. It would read around \(0^{\circ}\)C. Now, if you heat the mixture, you will find that its temperature does not rise until all the ice has melted. All the energy goes into changing ice to liquid water.

Since the transformation has occured with very little change in volume, the energy flow has been through heat. The amount of heat needed to melt the ice at \(0^{\circ}\)C is called the latent heat of melting of ice.

The same phenomenon occurs at the coexistence curve between any two phases. To develop a more general understanding of changing phases let us consider the constant pressure process abcde shown in the phase diagram Figure 22.4. At point a, the sample is entirely in solid. It has temperature \(T_a\) and pressure \(p_a\text{.}\) Now, we introduce some energy in the sample while keeping the pressure fixed. This can be done, for example, by heating the sample. The temperature and volume of the sample will change but we keep the pressure unchanged. If the process is conducted slowly then the sample will be in equilibrium and the temperature will change along the line \(ab\) in the diagram.

Figure 22.4. A constant pressure process in a phase diagram a-b-c-d-e illustrates the phase change at the co-existence points b and d along the way in the process.

The temperature reaches \(T_b\) with pressure \(p_a\) is an equilibrium condition for the coexistence of solid and liquid phases. As more energy is put into the system, the energy goes into loosening the molecules rather than raising the temperature. Note that raising the temperature is not possible since at point \(p=p_a\) and \(T>T_b\) the material does not exist in the solid phase. Therefore, at point b as we put more energy in the system, the sample must all first melt into the liquid phase. The energy that goes into transforming the substance from the solid phase to the liquid phase per unit mass of the material is called the specific latent heat of melting.

Once the material has completely melted at point b any additional energy in the material would raise the temperature of the material. since pressure is kept constant, the subsequent equilibrium conditions of the material will follow the path bcd in the liquid phase. During the bcd the temperature of the liquid will rise from \(T_b\) to \(T_d\) but the pressure will still be \(p_a\text{.}\) The liquid will normally expand during this process.

At the point d, the situation is similar to the point b. At the right of the point d, the material cannot exist in the liquid phase. Therefore, when we put more energy in the sample in the liquid phase at point d, the material transforms from the liquid phase into the gas phase. This transformation continues with each additional energy till all the material has been transformed from the liquid phase into the gas phase. The energy for the transformation from the liquid phase to the gas phase per unit mass is called the specific latent heat of evaporation.

After the material has turned completely into the gas phase at the point d, any additional energy put in the system would raise the temperature of the system. The system will successively progress in the line de of equilibrium states on the phase diagram. The energetics of the entire process a-e for ice-to-steam is shown in Fig. Figure 22.5 where heat is used to input energy in the system consisting a fixed amount of water in different phases at constant pressure.

Figure 22.5. Converting ice from below freezing to steam above boiling at constant pressure. The temperature of the ice changes approximately linearly with heat input when ice is below freezing, i.e., below \(0^{\circ}\)C at 1 atm pressure. At freezing temperature, the temperature dos not rise until all ice is converted into liquid water at freezing temperature. The temperature of the liquid water rises from \(0^{\circ}\)C to \(100^{\circ}\)C with input heat. At the boiling point, the temperature does not rise until all liquid is converted into steam. The slopes of \(Q\) vs temperature for ice, water and steam lines for a system containing \(1\text{ kg}\) of water correspond to their specific heats.

Specific latent heats of some common substances are given in Table 22.6. If the specific latent heat of a substance for a particular transformation is \(l \text{ J/kg} \text{,}\) then, to transform \(m \) kg of the material heat \(Q\) involved can be given by the following formula.

\begin{equation} Q = m\, l,\tag{22.4} \end{equation}

where \(Q\) will be positive if heat is being supplied to the system and negative if taken away from it.

Table 22.6. Latent heats of some common substances. The melting and boiling temperatures are at 1 atm pressure

Substance	Heat of	Melting	Heat of	Boiling
	of fusion	Temperature	of evaporation	Temperature
	(kJ/kg)	(K)	(kJ/kg)	(K)
Water	334	273.15	2258	373.15
Nitrogen	25	63.15	199	77.15
Mercury	11	234.15	294	630.15
Hydrogen	60	14.15	449	20.15

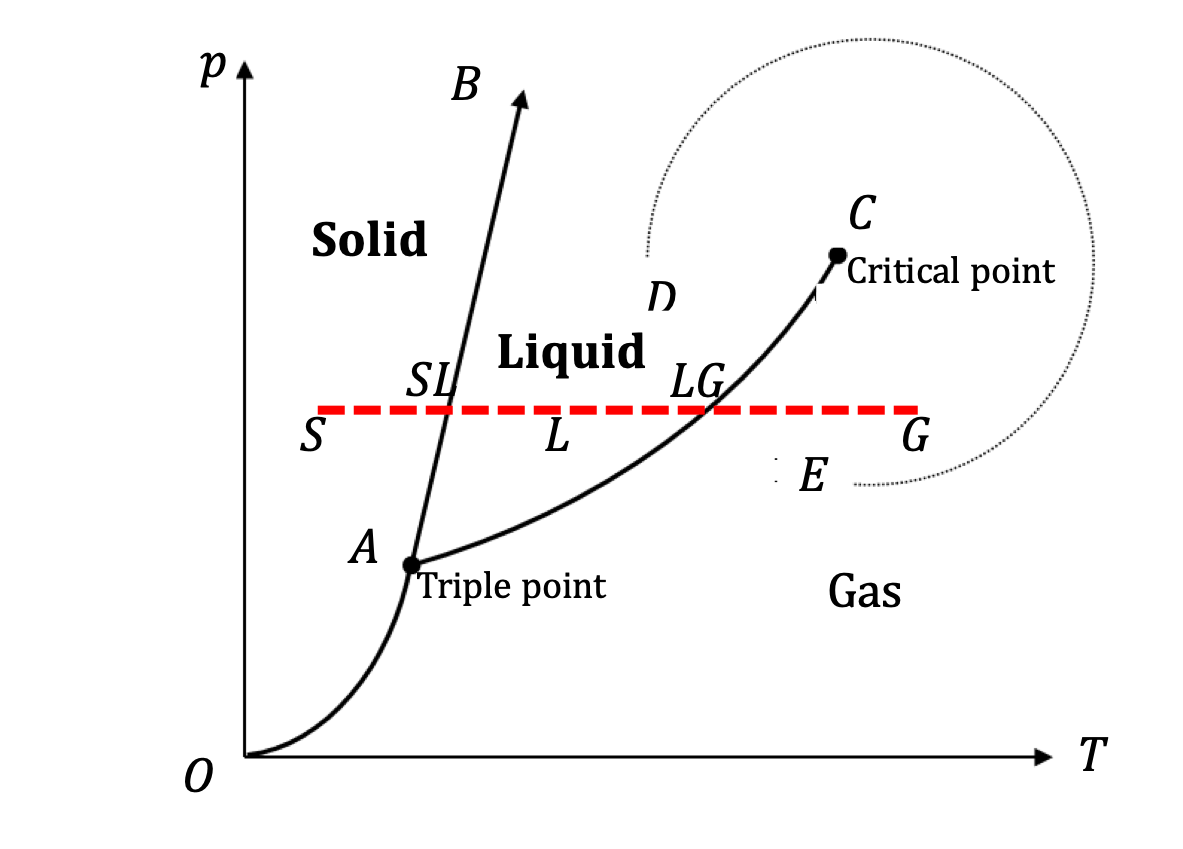
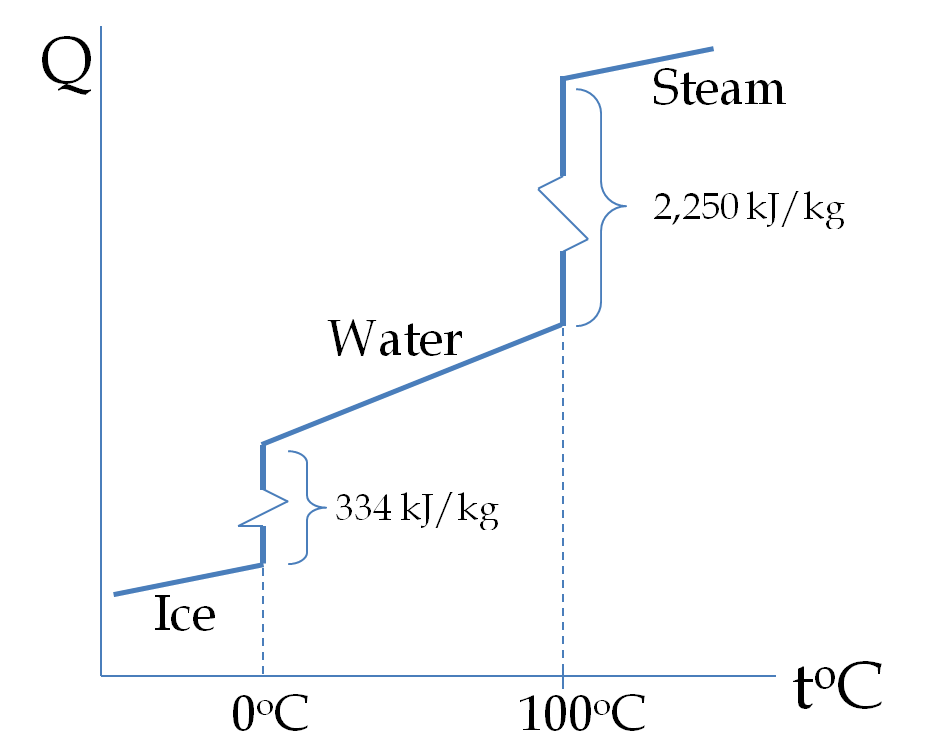
Example 22.7. Heat Needed to Convert Ice to Water Vapor at High Temperature.

You place \(10\text{-kg}\) of snow (ice) at \(-5^\circ\text{C}\) in a container with movable piston so that pressure inside the container is same as the pressure outside, which is 1 atmosphere. How much heat will be required to convert this ice to steam at \(550^\circ\text{C}\text{?}\)

Data: \(c_{P,\text{Ice}} = 2,090\text{ J/kg.}^\circ\text{C}\text{,}\) \(c_{P,\text{liquid water}} = 4,180\text{ J/kg.}^\circ\text{C}\text{,}\) \(c_{P,\text{water vapor}} = 1,860\text{ J/kg.}^\circ\text{C}\text{,}\) \(l_\text{ice/water} = 334,000\text{ J/kg}\text{,}\) \(l_\text{water/vapor} = 2,258,000\text{ J/kg}\text{.}\)

Answer.

\(38.6 \text{ MJ}\text{.}\)

Solution.

As we heat sample of ice, we will increase its temperature till we reach \(0^\circ\text{C}\text{.}\) The heat in this step will be obtained by \(Q=mc\Delta T\text{,}\) i.e., using specific heat. At \(0^\circ\text{C}\text{,}\) the phase transformation to liquid will take place. The heat in this step will be from \(Q= m l\text{.}\) Once fully transformed into liquid, more heat will raise the temperature till we get to \(100^\circ\text{C}\text{.}\) This step will use \(Q=mc\Delta T\text{.}\) Then trnasformation to steam and raising of temperature of steam, which will use \(Q= m l\) and \(Q=mc\Delta T\text{,}\) respectively. Let us suppress units in the expression below.

\begin{align*} Q \amp = 10\times 2,090 \times (0 - (-5)) \\ \amp \ \ \ + 10\times 334,000 \\ \amp \ \ \ + 10\times 4,180 \times (100 - 0) \\ \amp \ \ \ + 10\times 2,258,000 \\ \amp \ \ \ + 10\times 1,860 \times (550 - 100) \end{align*}

This gives

\begin{align*} Q \amp = 104,500 + 3,340,000 + 4,180,000\\ \amp \ \ \ + 22,580,000 + 8,370,000\\ \amp = 38,574,500 = 38.6 \text{ MJ}. \end{align*}

Example 22.8. Heat to Melt Copper.

How much heat is needed to melt \(10\text{ kg}\) of copper that is initially at \(25^{\circ}\text{C}\text{?}\)

Data: Melting point of copper = \(1,083^{\circ}\text{C}\text{,}\) heat of melting of copper = \(49130\text{ J/kg}\text{,}\) Specific heat of copper = \(390\text{ J per kg per deg C}\text{.}\)

Answer.

\(4,617,500\ \textrm{J}.\)

Solution.

First we need energy to raise the temperature, and then, additional energy to change the phase from the solid phase to the liquid phase at the melting point. Let \(Q_1\) and \(Q_2\) be the energy for the change in temperature and change in phase respectively. During the entire process the work is zero since the volume change is negligible. Therefore, the energy is all as heat and we use specific heat and heat of transformation to estimate the energy in the two processes.

\begin{align*} Q_1 \amp = m c \Delta T. \\ Q_2 \amp = m l. \end{align*}

Numerically, we will get the following,

\begin{align*} Q_1 \amp = 10\ \textrm{kg}\times 390 \frac{\textrm{J}}{\textrm{kg.}\ ^{\circ}\textrm{C}}\times (1083-25)\ ^{\circ}\textrm{C}\\ \amp = 4,126,200\ \textrm{J}. \\ Q_2 \amp = 10\ \textrm{kg}\times 49130 \textrm{J/kg} = 491,300\ \textrm{J}. \end{align*}

Net energy

\begin{equation*} Q = Q_1 + Q_2 = 4,617,500\ \textrm{J}. \end{equation*}

Exercises 22.2.4 Exercises

1.

How much heat is needed to melt \(10\, \text{kg}\) of iron that is initially at \(25^{\circ}\text{C}\text{?}\) Melting point of iron = \(1538^{\circ}\text{C}\text{,}\) heat of melting of iron = \(247000\, \text{J/kg}\text{,}\) Specific heat of iron = \(450\, \text{J/kg.C}\text{.}\)

Prev Top Next