Section 49.2 The Michelson-Morley Experiment
Before Einstein, it was a common assumption that there is some absolute frame with respect to which we can study all motion. The study of propagation of light challenged this assumption. The most seminal experiment was the Michelson-Morley experiment.
In the late nineteenth century scientists had difficulty believing that electromagnetic waves could travel through vacuum. They hypothesized that there must be some sort of medium in empty space whose oscillations helps light propagate. This medium was called ether. But how can we test this hypothesis?
If ether exists everywhere, then Earth must be traveling through ether. As a result, velocity of light relative to Earth will be different for light traveling in the same direction as Earth versus in the opposite direction. Assuming Galilean transformations apply, we will have the following relation between velocity \(\vec c^{\:\prime}\) of light relative to Earth, velocity \(\vec V\) of Earth relative to the ether, and velocity \(\vec c\) of light relative to ether.
\begin{equation}
\vec c^{\:\prime} = \vec c - \vec V.\tag{49.12}
\end{equation}
Here \(c = 3\times 10^8\text{ m/s}\text{.}\) Thus, if light travels in the same direction as the motion of the Earth, then the speed of light in the Earth-frame will be \(c'=c-V\) and if the light beam travels in the opposite direction, it will be \(c'=c+V\text{.}\)
\begin{align}
\amp \textrm{Light in same direction as Earth, }\ \ c'=c-V \nonumber\tag{49.13}\\
\amp \textrm{Light in opposite direction as Earth, }\ \ c'=c+V \tag{49.14}
\end{align}
A. A. Michelson, who had invented the optical interferometer that bears his name, analyzed what will happen in his interferometer if one arm of the interferometer was parallel and the other arm was perpendicular to the direction of the motion of the Earth. He noted that he needed a sensitivity of \((V/c)^2 = 10^{-8}\) to detect the effect. His instrument was more than capable of giving this high a sensitivity.
Michelson conducted his experiments in 1881 and repeated with E. W. Morely in 1887. Both times he was disappointed to find no difference in his results which pointed to \(c' = c\text{,}\) that is, as if speed of light with respect to ether and with respect to Earth were the same or some other weird thing was taking place!
Subsection 49.2.1 Michelson-Moreley Experiment
A sketch of the Michelson interferometer is shown in Figure 49.12. A beam of light is incident on a half-silvered mirror M, also called the beam splitter, which is incline at \(45^{\circ}\) to the incoming beam. The beam splitter splits the beam into two, one of which is transmitted (beam 1) and the other reflected (beam 2) at \(90^{\circ}\) to beam 1. Beams 1 and 2 reflect off mirrors M\(_1\) and M\(_2\) respectively. The returning beam 1 is partially reflected off the beam splitter in the direction of the telescope and beam 2 is partially transmitted through the beam splitter towards the telescope where the two beams overlap and interfere. If the mirrors M\(_1\) and M\(_2\) are not exactly perpendicular, one sees bright and dark fringes in the telescope as shown in the figure depending on the phase difference between the two beams.
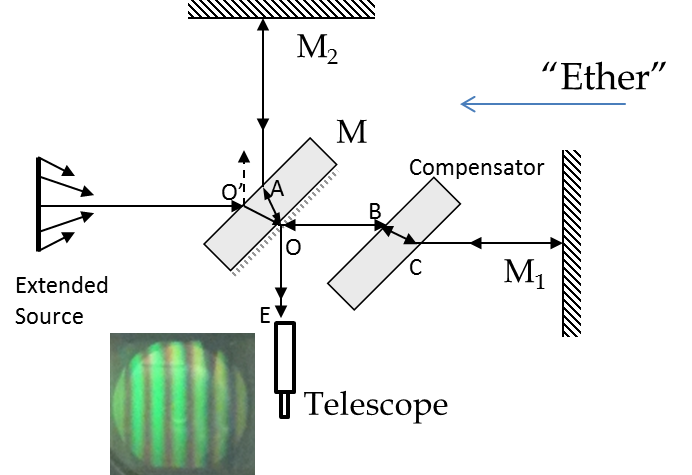
At a place where the phase difference is an integer multiple of \(2\pi\text{,}\) we see the bright fringe and where the phase difference is an odd integer multiple of \(\pi\) we see the dark fringe. To work out the phase difference let us work out the time of travel in the two paths. Let \(\Delta t_1\) and \(\Delta t_2\) be the times for the two beams in their round trips MM\(_1\)M and MM\(_2\)M respectively. Let the arm lengths of the two sides be \(l_1\) and \(l_2\text{.}\) When beam 1 is parallel to the direction of motion of the Earth, one half of the path of beam 1 will be downstream and the other half upstream with speeds \(c+V\) and \(c-V\) respectively, where \(c\) is the speed of light relative to the purported ether, and \(V\) the speed of Earth relative to the ether. Therefore, the time \(\Delta t_1\) will be
\begin{align}
\Delta t_1 \amp = \dfrac{l_1}{c+V} + \dfrac{l_1}{c-V} = \dfrac{2l_1/c}{1- V^2/c^2}\notag\\
\amp \approx \dfrac{2l_1}{c}\left(1+\dfrac{V^2}{c^2} \right),\tag{49.15}
\end{align}
where I have expanded the final expression in powers of \(V/c\) and kept terms only up to \(V^2/c^2\text{.}\) The time for beam 2 is a little tricky. When beam 2 leaves M, the mirror M\(_2\) is exactly in front of it, but during the time the light particles reach M\(_2\) the mirror will have moved to a different location. Similarly, on its return, the beam splitter M will have moved to a different place. Thus, MM\(_2\)M is not a straight path but is angled at M\(_2\text{.}\) The distance from M to M\(_2\) traveled by light is not equal to \(l_2\) but rather the hypotenuse of the triangle with base equal to \(\dfrac{V}{2}\Delta t_2\) and perpendicular equal to \(l_2\text{.}\) The hypotenuse will equal \(\dfrac{c}{2}\Delta t_2\) by using the speed of light perpendicular to the direction of motion of the Earth. Using Pythagora’s theorem we have
\begin{equation}
\left( \dfrac{c}{2}\Delta t_2 \right)^2 = \left( \dfrac{V}{2}\Delta t_2 \right)^2 + l_2^2.\tag{49.16}
\end{equation}
Solving for \(\Delta t_2\text{,}\) keeping only the positive root we get
\begin{equation}
\Delta t_2 = \dfrac{2l_2/c}{\sqrt{1- V^2/c^2}} \approx \dfrac{2l_2}{c}\left(1+\dfrac{V^2}{2 c^2} \right),\tag{49.17}
\end{equation}
where I have again expanded the final expression in powers of \(V/c\) and kept terms only up to \(V^2/c^2\text{.}\) Now, we obtain the difference between the travel times \(\Delta t\) of the two beams to be
\begin{equation}
\Delta t = \Delta t_1 - \Delta t_2 = \frac{2}{c}\left( l_1 - l_2\right) + \dfrac{V^2}{c^2}\left(2 l_1 - l_2 \right).\tag{49.18}
\end{equation}
If the arms were of equal length, \(l_1 = l_2 \equiv l\text{,}\) we will get
\begin{equation}
\Delta t = \dfrac{l}{c}\ \dfrac{V^2}{c^2}.\tag{49.19}
\end{equation}
A delay of time corresponding to a travel distance of one wavelength \(\lambda\) causes a phase difference of \(2\pi\) radians. therefore, this delay between the two paths will cause a phase difference \(\Delta \phi\) of
\begin{equation}
\Delta\phi = 2\pi\times \dfrac{c\Delta t}{\lambda} = \dfrac{l}{c}\ \dfrac{V^2}{c^2}.\tag{49.20}
\end{equation}
As an example consider \(l = 1\) m, \(\lambda = 5.89\times 10^{-7}\) m (the sodium yellow line), \(V = 3\times 10^{4}\) m/s (the orbital speed of Earth around Sun), \(c = 3\times 10^{8}\) m/s. The phase shift expected will be 0.11 rad or \(6.1^{\circ}\text{.}\) That is, if you were to stop the Earth, set up the reference fringe pattern, and then let the Earth move at 30 km/s with respect to ether, we will see a phase shift of 0.11 rad. But, there is a problem with this procedure - you cannot stop the Earth! To get around this problem, Michelson had an ingenious idea to exploit the symmetry in the two arms: If you rotate the apparatus by \(90^{\circ}\text{,}\) then beams 1 and 2 would switch positions with beam 2 now becoming parallel to the direction of the motion of the Earth. This will result in a change in delay \(\Delta(\Delta t)\) and one can watch how the fringes change.
\begin{equation}
\Delta(\Delta t) = \Delta t - \Delta t_{\perp} = \dfrac{2l}{c}\ \dfrac{V^2}{c^2}.\tag{49.21}
\end{equation}
If you have different arm lengths, we now get
\begin{equation}
\Delta(\Delta t) = \Delta t - \Delta t_{\perp} = \dfrac{l_1 + l_2}{c}\ \dfrac{V^2}{c^2}.\tag{49.22}
\end{equation}
As you rotate the apparatus, you will find that fringes move past cross-hair line of the telescope. For each change in delay of \(\lambda/c\text{,}\) one fringe will move past the cross-hair. Therefore, for the change in delay \(\Delta(\Delta t)\) the number of lines passing the cross-hair will be
\begin{equation}
N = \dfrac{\Delta(\Delta t)}{\lambda/c} = \dfrac{l_1 + l_2}{\lambda}\ \dfrac{V^2}{c^2}.\tag{49.23}
\end{equation}
In Michelson’s first experiment in 1881 the arm length was 1.2 m. With \(\lambda = 5.89\times 10^{-7}\) m (the sodium yellow line) and \(V/c = 10^{-4}\text{,}\) the predicted number of fringes moving during the rotation of the apparatus will be
\begin{equation}
N = \dfrac{2\times 1.2}{5.89\times 10^{-7}}\times 10^{-8} = 0.04.\tag{49.24}
\end{equation}
Michelson found no discernible shift in the fringe pattern when he rotated his apparatus. Michelson considered his experiment a flop since it failed to show the expected result. Six years later with the help of E. W. Morley he refined his apparatus so that the beams now reflected back and forth eight round trips, effectively making \(l_1 + l_2\) in Eq. (49.23) much longer, about 22 m. With sodium yellow light the expected fringe shift now was expected to be almost \(10 \times\) as large:
\begin{equation}
N = \dfrac{22}{5.89\times 10^{-7}}\times 10^{-8} = 0.37.\tag{49.25}
\end{equation}
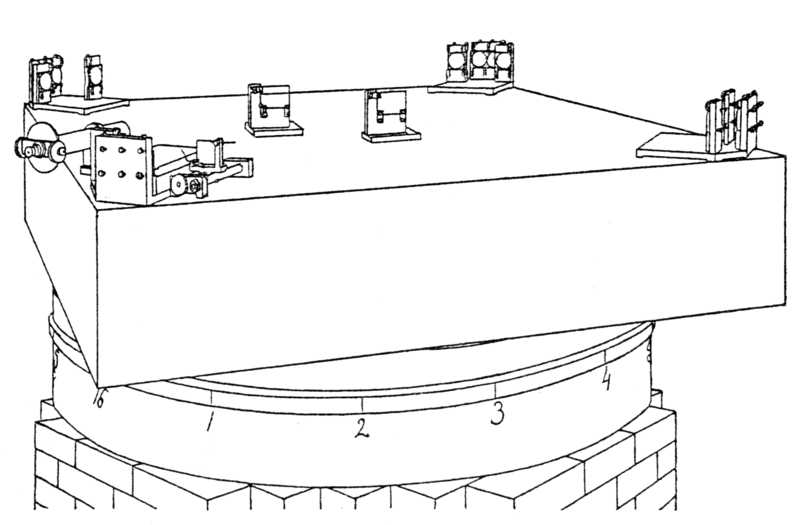
Michelson and Morley placed their apparatus on a heavy stone slab for stability and floated the slab on mercury so that the apparatus could be rotated continuously about a pin Figure 49.13. Their apparatus was stable enough to see a shift in fringes as small as \(N = 0.01\text{.}\) However, they were unable to detect any fringe shifts despite measurements during the day, during the night, and at different times of the year. This null result is celebrated in physics as the most successful failed experiment!
Lessons from the “Failure” of Michelson-Morley Experiment
What can one conclude from the failure of Michelson and Morley to detect the drift of ether? One conclusion may be that there is no ether and the speed of light is same with respect to all observers. This conclusion at the time appeared to be too radical since it violated well-established notions of Galilean relativity. Several hypotheses were proposed to save the ideas of ether and Galilean relativity but each had some problems which could be demonstrated by experiment. Einstein working apparently without the knowledge of the Michelson-Morley experiment came to the conclusion that speed of light was same for all inertial observers. Before we study Einstein’s relativity we will take a look at some aspects of Newtonian mechanics that are the fundamental sources of trouble.

