Fluid Flow

Section 18.1 Fluid Flow

Subsection 18.1.1 Flow in a Pipe

Turn on the faucet and collect water in a bucket. Suppose it takes \(15\text{ sec}\) to fill a \(4\text{-liter}\) bucket. Dividing the volume by the time, i.e., \(16\text{ liter/min} \text{,}\) gives us an important measure of flow, called the volume rate of flow. This is denoted by letter \(Q\text{.}\)

\begin{equation} Q = \dfrac{\Delta V}{\Delta t}\tag{18.1} \end{equation}

We can also speak of the speed of flow, \(v\text{,}\) by looking inside the pipe. Observe that all the fluid that was within a distance of \(v\Delta t\) would have gone to the bucket in time \(\Delta t\text{.}\) That is, if the cross-section of the pipe is \(A \text{,}\) then, the volume flowed is

\begin{equation} \Delta V = A v\Delta t.\tag{18.2} \end{equation}

Using this in Eq. (18.1) we find the relation between the two measures of flow, viz., volume rate of flow and the speed of flow.

\begin{equation} Q = A v.\tag{18.3} \end{equation}

On multiplying \(Q \) by the density of the fluid, \(\rho\text{,}\) we will get the mass rate of flow. The mass rate of flow is also called current. It is usually denoted by letter \(I\text{.}\)

\begin{equation} I = \rho Q = \rho A v.\tag{18.4} \end{equation}

When we divide current by the area of cross-section \(A\text{,}\) we get current density, denoted by \(J\text{.}\)

\begin{equation*} J = \dfrac{I}{A} = \rho\,v. \end{equation*}

Subsection 18.1.2 Incompressibility and Steady Flow

When the volume flow rate \(Q = Av\) is same throughout and not changing with time, we say that the fluid flow is steady. An object is incompressible if volume change is negligible when you compress the object. Below, we derive an important relation for an incompressible fluid flow.

To study analytically, let us consider a steadily flowing incompressible fluid in a pipe whose cross-section varies as shown in Figure 18.1.

Figure 18.1. Incompressibility of the fluid in a steadily flowing fluid implies that the volume of liquid entering the space between 1 and 2 at 1 must equal the volume leaving at 2.

Let \(A_1\) and \(A_2\) be the cross-sectional areas of the entrance and exit respectively, and \(v_1\) and \(v_2\) be the corresponding speeds. In time \(\Delta t \text{,}\) all fluid within a volume \(A_1 v_1 \Delta t \) would have entered the space between 1 and 2, and during this time all fluid within a volume \(A_2 v_2\Delta t \) would have exited the space. Equating the two, and canceling out \(\Delta t\) gives the following important result, which is sometimes called the equation of continuity.

\begin{equation} A_1 v_1 = A_2 v_2.\tag{18.5} \end{equation}

This says that the fluid will be faster (higher \(v \)) in the narrower part (ie., where \(A\) is smaller) and vice-versa.

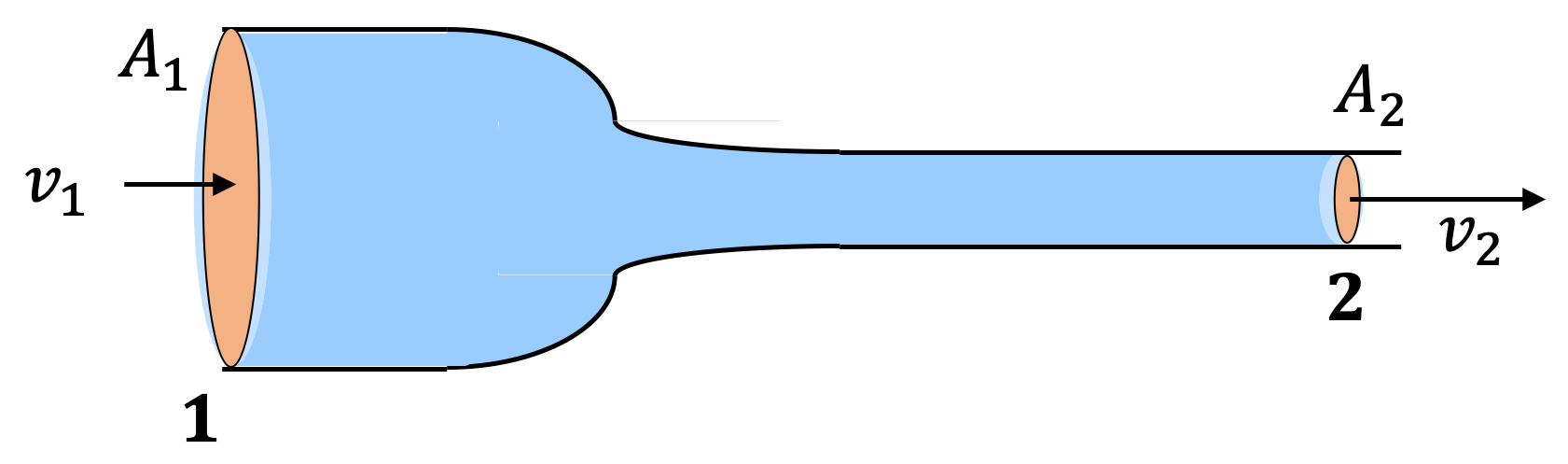
Example 18.2. Volume and Mass Flow Rates in a Cylindrical Pipe.

Water flows through a cylindrical pipe of internal diameter \(1.0\text{ cm}\text{.}\) (a) If \(1000\text{ L}\) of water flows per minute, what is the velocity of flow in \(\text{m/s}\text{?}\) (b) What is the mass rate of flow in \(\text{kg/s}\text{?}\)

Data: \(\rho_w = 1000\text{ kg/m}^3\text{.}\)

Answer.

(a) \(212\text{ m/s}\text{,}\) (b) \(16.7\text{ kg/s}\text{.}\)

Solution 1. (a)

(a) Let us work with SI units \(\text{(m, kg, s)}\text{.}\)

\begin{align*} R \amp = 0.5\times 10^{-2}\text{ m}, \\ A \amp = \pi R^2 = 7.85\times 10^{-5}\text{ m}^2 \\ Q \amp = 1000\dfrac{\text{L}}{\text{min}} = \dfrac{1.0}{60}\text{ m}^3\text{/s}. \end{align*}

Therefore,

\begin{equation*} v = \dfrac{Q}{A} = 212\text{ m/s}. \end{equation*}

Solution 2. (b)

(b) By multiplying \(Q\) by \(\rho\text{,}\) the density, we will get the mass current.

\begin{equation*} \rho_w Q = 16.7\text{ kg/s}. \end{equation*}

Example 18.3. Varying Flow Speeds in a Garden Hose and Nozzle.

Your garden hose has an inner radius of \(0.65\text{ cm}\) and the nozzle through which water comes out has a radius of \(0.250\text{ cm}\text{.}\) You are watering the lawn with \(40\text{ L}\) per minute.

(a) What is the speed of water in the hose?

(b) What is the speed of water in the nozzle?

Answer.

(a) \(5.0\text{ m/s}\text{,}\) (b) \(33.8\text{ m/s}\text{.}\)

Solution 1. (a)

(a) We need the area of cross-section of hose.

\begin{equation*} A = \pi R^2 = \pi \times 0.65^2 = 1.327\text{ cm}^2. \end{equation*}

We work in \(\text{cm} \) units by converting \(1\text{ L}=1000\text{ cm}^3\) and in \(\text{s} \) by \(1\text{ min} = 60\text{ s}\text{.}\)

\begin{equation*} v = \dfrac{Q}{A} = \dfrac{40\times 1000}{60}\dfrac{1}{1.327} = 502.4\text{ cm/s} = 5.0\text{ m/s}. \end{equation*}

Solution 2. (b)

(b) Since \(Q \) is same, the velocity will only vary due to the areas.

\begin{equation*} v_{\text{nozzle}} = \dfrac{A_{\text{hose}}}{A_{\text{nozzle}}}\ v_{\text{hose}}. \end{equation*}

We do not need to find the individual areas since we need only their ratio, which wil lbecome ratio of their radii squared.

\begin{equation*} v_{\text{nozzle}} = \left( \dfrac{0.65}{0.250} \right)^2 \, 5.0 = 33.8\text{ m/s}. \end{equation*}

Subsection 18.1.3 (Calculus) Current Density

Current per unit area of cross-section is called the current density. We defined current above by \(I = \rho A v\text{.}\) Dividing this by \(A \) we get the current density, which will be denoted by letter \(J\text{.}\)

\begin{equation} J = \rho v.\tag{18.6} \end{equation}

If the flow in a tube is not uniform, for instance, flow may be faster in the middle of the tube than near the edge, then current density will vary over the cross-section. Current density will also vary if density of the material varies. We then speak of current density as local current density, and can think of \(J\) as a function of position \((x, y, z) \text{.}\)

\begin{equation} J(x,y,z) = \rho(x,y,z) v(x,y,z).\tag{18.7} \end{equation}

Current density is a vector with magnitude given here and the direction in the direction of the flow.

If current density does not vary over the cross-section, then current is simply the product of current density and the area of cross-seciotn.

\begin{equation} I = JA\ \ \ \ (\text{if } J\text{ uniform,})\tag{18.8} \end{equation}

otherwise, we need to integrate current density over the cross-section area. This is written as a conceptual integral.

\begin{equation} I = \int\, J\, dA.\tag{18.9} \end{equation}

In a particular situation, you will need to decide how to write \(dA\text{.}\) In a rectangular cross-section, you might say \(dA=dxdy\) and in a circular cross-section, polar coordinates will be more appropriate with \(dA = rdrd\theta\text{.}\) If we have a circular symmetry, you might use \(dA=2\pi r dr\text{.}\)

Subsection 18.1.4 (Calculus) Laminar Flow in a Cylindrical Tube

It will not surprise you that fluid flows faster in the center than near the wall - this is what happens in a river where water flows faster in the middle and hardly any near the bank.

A more advanced treatment of fluid flow shows that at low speeds of flow, speed of flow at radial distance \(r\) from the center of a tube of radius \(R\) varies quadratically as shown diagrmatically in the figure on the right.

\begin{equation} v = v_0 - \dfrac{r^2}{R^2} v_0,\tag{18.10} \end{equation}

where \(v_0\) is the speed at the center.

To find current through the tube, we look at flow through a ring of infinitesimal area \(dA = 2\pi rdr\text{,}\) which is between radius \(r\) and \(r+dr\text{.}\) Let \(\rho\) be uniform density.

\begin{align*} I \amp = \int J\, dA = \int \rho v 2\pi rdr \\ \amp = 2\pi \rho v_0 \int_0^R \left( 1 - \dfrac{r^2}{R^2}\right) r dr \\ \amp = \dfrac{1}{2}\rho v_0 \pi R^2 = \dfrac{1}{2}\rho v_0 A. \end{align*}

Note that if the speed was \(v_0\) at all points of the cross-section, we would get \(2 \times \) as much current, but that is not what actually happens. You get only half as much flow as dictated by the speed at the center since fluid is flowing at different speeds across the cross-section.

Exercises 18.1.5 Exercises

1. Steady Flow of Water Through Pipes in a House.

A water supply pipe to a house has an internal diameter of 4 cm. The second floor of the house has water pipe of diameter 2 cm.

(a) If water flows at the speed of 10 m/s from the pipe at the second floor, what is the speed of flow in the supply line?

(b) What is the volume rate of flow?

Data: \(\rho_w = 1000\text{ kg/m}^3\text{.}\)

Hint.

(a) Use \(A_1v_1 = A_2v_2\text{,}\) (b) \(Q=Av\text{,}\) (c) \(I = \rho Q\text{.}\)

Answer.

(a) \(2.5\text{ m/s}\text{,}\) (b) \(3.14\text{ L/s}\text{,}\) (c) \(3.14\text{kg/s}\text{.}\)

Solution 1. (a)

(a) Using the speed of flow and the internal diameter for the pipe from the data for the second floor we find the volume rate of flow anywhere in the same pipe regardless the diameter of the pipe.

\begin{align*} Av \amp = \pi r^2 v = \pi\times (0.001\ \text{m})^2 \times 10\ \text{m/s}\\ \amp = \pi \times 10^{-5} \text{m}^3/\text{s}. \end{align*}

Now we can divide this by the area of cross-section of the supply line to find the speed of flow there.

\begin{align*} v_{\text{supply}} \amp = \dfrac{ \pi \times 10^{-5} \text{m}^3/\text{s}}{\pi (0.002\ \text{m})^2}\\ \amp = 2.5 \ \text{m/s}. \end{align*}

Better Way:

Although we have the correct answer here, but you may have noticed that there were quite a lot of cancellations in the calculations. In these calculations and actually many other places in physics putting the numbers right away is not a good idea. We should get to the final expression first before putting in the numbers. Let us do this problem again.

Let us label the quantities in the supply line with a subscript 1 and that in the second floor by the subscript 2. Then, we have

\begin{equation*} A_1 v_1 = A_2 v_2. \end{equation*}

We are looking for \(v_1\text{.}\) Let us solve for \(v_1\) and keep the ratio the same type of quanties together.

\begin{equation*} v_1 = \frac{A_2}{A_1} v_2. \end{equation*}

Note that keeping \(A_1\) and \(A_2\) together means that we do not need to worry about the particular units of \(A_1\) and \(A_2\) as long as they are both in the same units since the units will cancel out. Also any common factor will cancel out. Now we can write this formula in terms of the diameters.

\begin{equation*} v_1 = \left( \frac{d_2}{d_1} \right)^2 v_2. \end{equation*}

At this point we would plug in the numbers.

\begin{equation*} v_1 = \left( \frac{2 \ \text{cm}}{4\ \text{cm}} \right)^2 \times 10\ \text{m/s} = 2.5 \ \text{m/s}. \end{equation*}

Solution 2. (b)

(b) The volume rate of flow is \(Av\text{,}\) which can be determined from flow either in the supply line or the second floor.

\begin{equation*} A_2v_2 = \pi r^2 v = \pi\times (0.01\ \text{m})^2 \times 10\ \text{m/s} = 3.14 \times 10^{-3} \text{m}^3/\text{s}. \end{equation*}

Solution 3. (c)

(c) The current in the present context refers to the mass rate of flow which would be equal to the product of the volume rate of flow and the density.

\begin{equation*} \text{Current},\ A_2v_2 \rho = 3.14\ \text{kg}/\text{s}. \end{equation*}

2. Flow in a Branching System - The Human Circulatory System.

In a human circulatory, the Cardiac output flows through a large number of capillaroes. By one estimate a cardiac output of \(4.7\text{ L/min}\) branches out into \(5\times 10^{9}\) capillaries, each of diameter, approximately \(10\,\mu\text{m}\text{.}\)

(a) What is the blood flow speed in the capilalries?

(b) If the cadiac output is modeled to have a diameter of \(1.5\text{ cm}\text{,}\) what is the average speed of blood flow in the heart?

Hint.

(a) Add the flow rates of all capillaries.

Answer.

(a) \(0.2\text{ mm/s}\text{,}\) (b) \(1.4\text{ m/s}\text{.}\)

Solution 1. (a)

(a) The volume flow rates of capillaries must add up to the net cardiac output. For convenience, we work in the \(\text{m} \) units.

\begin{align*} \amp Q = 4.7\text{ L/min} = 7.8\times 10^{-5}\text{ m}^3\text{/s},\\ \amp A_{\text{cap}} = \pi\times 5^2 \times 10^{-12} = 7.85\times 10^{-11}\text{ m}^2.\\ \amp A = N_{\text{cap}} A_{\text{cap}} = 0.392\text{ m}^2. \end{align*}

\begin{align*} v \amp = \dfrac{Q}{N_{\text{cap}}A_{\text{cap}}} = \dfrac{7.8\times 10^{-5}}{0.392 }, \\ \amp = 0.000199\text{ m/s} = 0.2\text{ mm/s}. \end{align*}

Solution 2. (b)

(b) We just need to scale with respect to areas. Let us use subscript 1 for the arteries and 2 for the capillaries.

\begin{align*} v_1 \amp = \dfrac{N_2A_2}{A_1} v_2 = \dfrac{0.392}{\pi (0.75\times 10^{-2})^2}\, 0.2\text{ mm/s} \\ \amp = 1400\text{ mm/s} = 1.4\text{ m/s}. \end{align*}

3. Computing Current Density.

Rate of mass flow per unit area is also called current density \(J\text{.}\) Find the current density of water flowing through a cylindrical pipe of diameter \(5\, \text{cm}\) at the rate of \(100\, \text{L}\) per second.

Answer.

\(5.1 \times 10^4\ \text{kg/m}^2.s\text{.}\)

Solution.

First, let’s take care of units by expressing all units in the SI system. It helps to recall that \(1000\, \text{L}\) makes \(1\, \text{m}^3\text{.}\)

\begin{align*} J \amp = \frac{\rho \times \textrm{Volume Flow Rate}}{A} \\ \amp = \frac{1000\ \textrm{kg/m}^3 \times 0.1\ \textrm{m}^3/\textrm{s} }{\pi\times (0.025\ \textrm{m})^2} = 50,900\ \textrm{kg/s.m}^2. \end{align*}

Prev Top Next