Electric Field for Planar Symmetry

Section 30.5 Electric Field for Planar Symmetry

Subsection 30.5.1 Planar Symmetry

A planar symmetry of charge density is obtained when charges are uniformly spread over a large flat surface as shown in Figure 30.28. Mathematically, we require the planar surface to be infinite in extent in all directions of the plane, e.g., entire \(xy\)-plane, with surface charge density (SI units: \(\text{C/m}^2\)) same everywhere on the plane.

Figure 30.28. Charges distributed uniformly on a plane are represented in a three-dimension perspective or as an edge view.

Subsection 30.5.2 Consequences of Planar Symmetry

Suppose the plane of charges is the \(xy\)-plane. Now, what can we say about electric field at some point P above the plane, say on the \(z\) axis?

Direction of the Field:

One way to think about how to get that is to superimpose electric fields by every charge.

Now, take a look at the electric field by an arbitrary charge in the plane, say at \((x,y)\text{.}\) It is at an angle to the vertical. But, for every charge there is an equal charge on the plane, here \((-x,-y)\text{,}\) whose electric field cancels out the horizontal component of electric field at P.

Therefore, we can assert that electric field will be pointed vertically to the plane. If the charges are positive, electric field will be away from the plane and if the charges are negative, electric field will be pointed towards the plane.

Magnitude of the Field:

Since the plane of charge is infinite along \(x\) and \(y\) axes, two points \(P_1\) and \(P_2\) at same \(z\) coordinate but different \((x,y)\) coordinates are at the same physical situation from the plane.

Figure 30.29. The magnitude of electric field in a planar symmetry situation can depend only on the distance from plane. We expect electric fields at points \(P_1\) and \(P_2\) to be equal.

Therefore, we do not expect elctric field to depend on \((x,y)\) coordinates. We expect that the magnitude of the elctric field can, at most, depend on the distance of the field point from the plane.

\begin{equation*} E(x,y,z) = E(z). \end{equation*}

We will find below that, even that dependence is not there. We will find that elctric field has a constant magnitude everywhere. Let’s see how.

Subsection 30.5.3 Electric Field of a Uniformly Charged Plane Sheet

Electric field of a charged plane sheet such as shown in Figure 30.28 is constant. LEt \(\sigma\) be charge per unit area of the plane. Then, we will prove below that electric field has a constant magnitude every where.

\begin{equation} E = \frac{\sigma}{2\epsilon_0}.\tag{30.23} \end{equation}

This is an important result to remember since we do find many situation in which a planar charge approximation can be applied.

The direction of the field depends on its location. For instance, for positively charged sheet, the direction is up above the plane and down below the plane. For negatively charged sheet, the direction is towards the sheet. Electric field lines are perpendicular to the sheets.

Figure 30.30. Direction of electric field near charged sheets.

Subsection 30.5.4 Derivation of Electric Field by Gauss’s Law

Gaussian Surface and Flux

You should know by now that when we apply Gauss’s law, we seek to find a Gaussian surface so that electric field inside the integral of flux calculation can come outside of the integral. We take the same analysis path here as we did for spherical and cylindrical cases.

Suppose charges are in the \(xy\)-plane. Then, by discussion above, we can say that electric field will have the following form.

\begin{equation*} \vec E = E(z)\hat u_z, \end{equation*}

where I am using \(\hat u_z\) for unit vector towards positive \(z\)-axis.

A Gaussian surface that makes use of these obervations about the electric field has the shape of a box that straddles the charges plane symmetrically as shown in Figure 30.31. Since the top and bottom of the box are same distance from the plane, electric field has same magnitude at top and bottom. We will denote this by \(E_P\text{.}\)

Figure 30.31. The Gaussian surface is the surface of the closed box straddling the charged sheet in the plane. Our interest is to find electric field at point P, which is a point on the top side of the box. The normal to each face of the box is from inside the box to outside.

Recall that direction of normal vectors for a closed surface are taken from inside-to-outside. Therefore, we find that in the top and bottom parts, electric field and normal are in the same direction, but they are perpendicular to each other at other parts of the box. Let \(A\) be the area at the top and bottom. Therefore, flux through the surfaces of the closed box will be

\begin{equation} \Phi_\text{through box} = E_P A + 0 + 0 + 0 + 0 + E_P A = 2E_P A,\tag{30.24} \end{equation}

where zeros refer to the sides of the box other than top and bottom. Now, we find the enclosed charge to mae use of Gauss’s law.

Enclosed Charge:

When we look inside the box, we find that charge on area \(A\) of the sheet is inside the box. This is the enclosed charge. Since surface density of charge is \(\sigma\text{,}\) we get

\begin{equation} q_\text{enc} = \sigma A.\tag{30.25} \end{equation}

Use Gauss’s Law:

Now, we use expressions for flux and enclosed charge in Gauss’s law to get

\begin{equation*} 2 E_P A = \frac{\sigma A }{\epsilon_0}. \end{equation*}

This gives the magnitude of electric field at point P to be

\begin{equation} E_P = \frac{\sigma}{2\epsilon_0}.\tag{30.26} \end{equation}

This field does not depend on how far P is from the plane. The direction of electric field does depend on which side of the plane you are looking at. In Figure 30.31, the direction is \(+\hat u_z\) at points with \(z\gt 0\) and \(-\hat u_z\) at points with \(z\lt 0\) as reproduced again in Figure 30.32.

Figure 30.32. Field lines for positively and negatively charged planar charges are illustrated. The magnitude of electric field has a constant values \(E=\sigma/2\epsilon_0\) at all points.

Exercises 30.5.5 Exercises

1. Surface Charge Density on a Uniformly Charged Sheet from Given Electric Flux.

The electric flux through a square shaped area of side 5 cm near a large charged sheet is \(3 \times 10^{-5}\ \text{N.m}^2/\text{C}\) when the area is parallel to the plate. (a) Find charge density on the sheet. (b) How strong is the electric field at the location of the square area?

Hint.

(a) Use the electric field formula to find the flux. (b) Use definition of flux.

Answer.

(a) \(2.12 \times 10^{-13}\: \text{C/m}^2\text{,}\) (b) \(0.012\text{ N/C} \text{.}\)

Solution 1. (a)

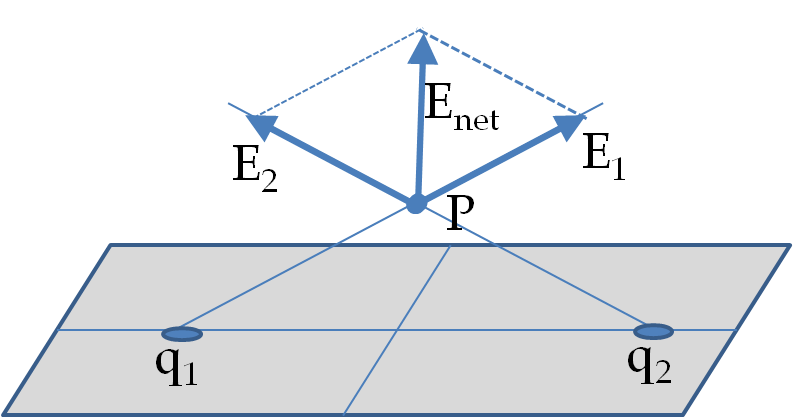
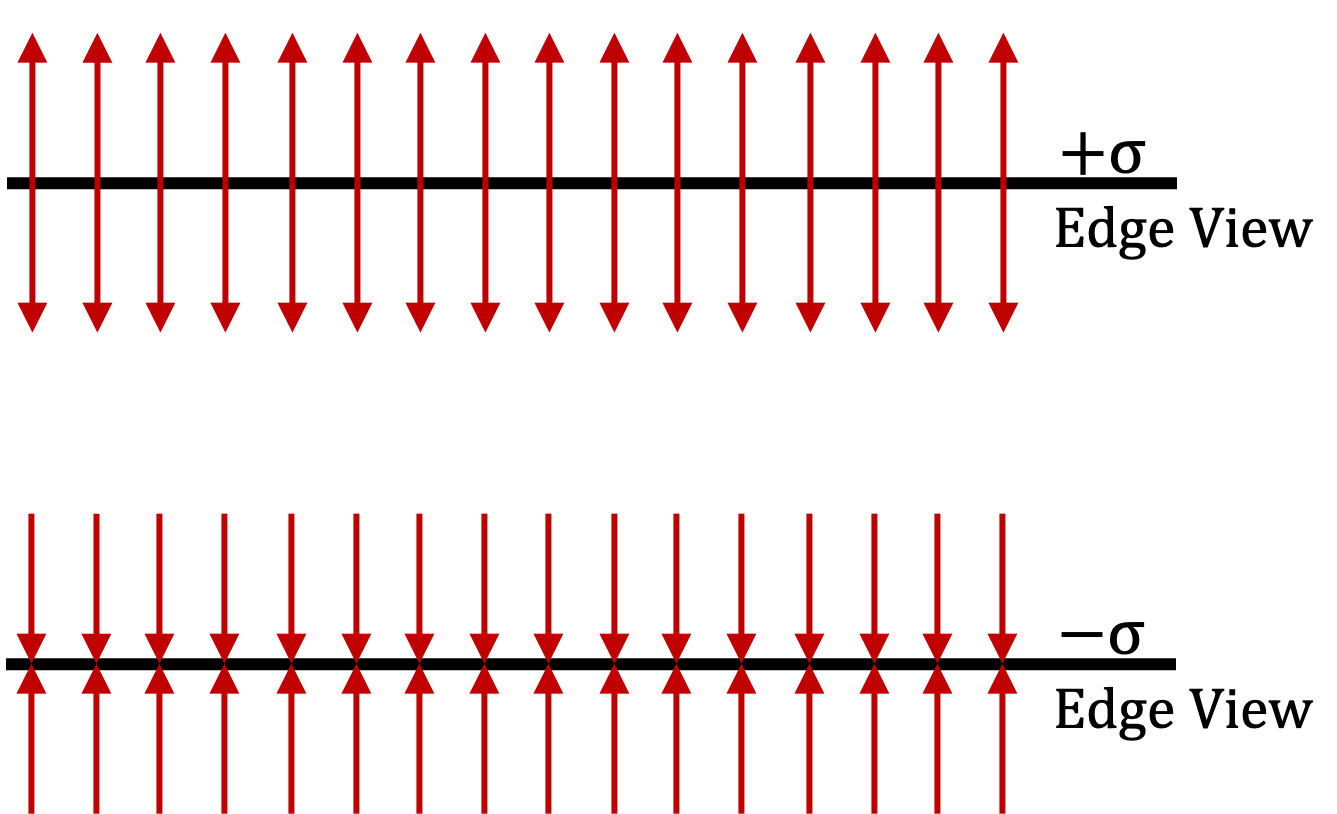
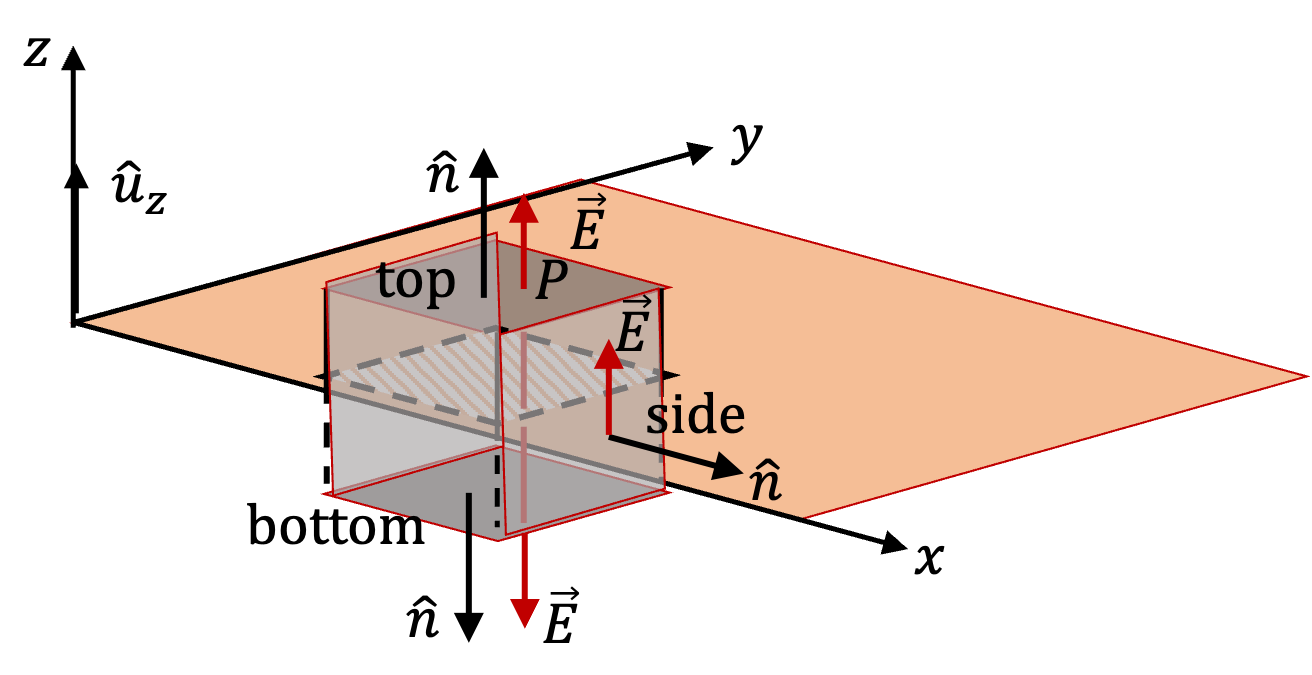
Let \(\sigma\) be the charge density on the large sheet. Since the sheet is large, we will assume it be infinitely large. This will make the the charge distribution to have planar symmetry. We can then, either present the arguments presented above in this section, or just borrow the final answer.

Borrowing the final answer for the magnitude of the field, we have

\begin{equation*} E = \dfrac{\sigma}{2\epsilon_0}, \end{equation*}

which is constant and the drection is perpendicular to the sheet. Therefore, the flux will be

\begin{equation*} \Phi = E\: A\:\:\cos\: 0^{\circ} = E A = \frac{\sigma}{2\epsilon_0}A. \end{equation*}

Hence, the surface charge density will be

\begin{align*} \sigma \amp = \frac{2\epsilon_0\:\Phi}{A} \\ \amp = \frac{2\times 8.85\times 10^{-12}\times 3 \times 10^{-5}}{0.05^2} = 2.12 \times 10^{-13}\: \text{C/m}^2. \end{align*}

Solution 2. (b)

We will just divide the flux by the area to get the field since field is constant over the area.

\begin{equation*} E = \frac{\Phi}{A} = \frac{3 \times 10^{-5}\ \text{N.m}^2/\text{C}}{0.05^2\text{ m}^2} = 0.012\text{ N/C}. \end{equation*}

2. Electric Flux Through Tilted Area from Electric Field of Two Oppositely Charged Plates.

Two large rectangular aluminum plates of area \(150\ \textrm{cm}^2\) face each other with a separation of 3 mm between them. The plates are charged with equal amount of opposite charges, \(\pm 20\: \mu \textrm{C}\text{.}\) The charges on the plates face each other. Find the flux through a circle of radius 3 cm between the plates when the normal to the circle makes an angle of \(30^{\circ}\) with a line perpendicular to the plates.

Hint.

First find the electric field of the two plates together, and then account for the area of the circle not being perpendicular to the electric field.

Answer.

\(\pm 3.67\times 10^{5}\ \text{N.m}^2/\text{C}\text{.}\)

Solution.

First we note that in the space between the plates, the electric fields of the charges on the two plates will add to give the magnitude

\begin{equation*} E = \dfrac{\sigma}{2\epsilon_0} + \dfrac{\sigma}{2\epsilon_0} = \dfrac{\sigma}{\epsilon_0}, \end{equation*}

with direction from the positive plate to the negative plate. Problem gave us charge and the area of the plate over which the charge was spread. From this we compute \(\sigma\) to be

\begin{align*} \sigma \amp = \dfrac{Q}{A_{\text{plate}}} = \dfrac{20\, \mu\text{C}}{150\ \text{cm}^2} = 1.33\times 10^{-3} \text{C/m}^2. \end{align*}

This gives the value of the magnitude of the electric field to be

\begin{equation*} E = \dfrac{1.33\times 10^{-3} } {8.85\times 10^{-12} } = 1.5\times 10^8\text{ N/C}. \end{equation*}

Next, we note that, since the electric field is normal to the plates, the electric field will make an angle \(\theta=30^\circ\) with the normal to the area, i.e., with the area vector. That will mean the flux will be reduced by \(\cos\,\theta\text{.}\) Since electric field is constant, we do not need to do any integration, we can just multiply the electric field magnitude and effective area.

\begin{equation*} \Phi = E\; A\; \cos\,\theta. \end{equation*}

Putting in numerical values, we get

\begin{align*} \Phi \amp = 1.5\times 10^8\times \pi\times 0.03^2 \times \cos\,30^\circ\\ \amp = 3.67\times 10^{5}\: \text{N.m}^2/\text{C}. \end{align*}

Prev Top Next