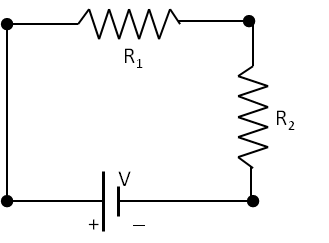
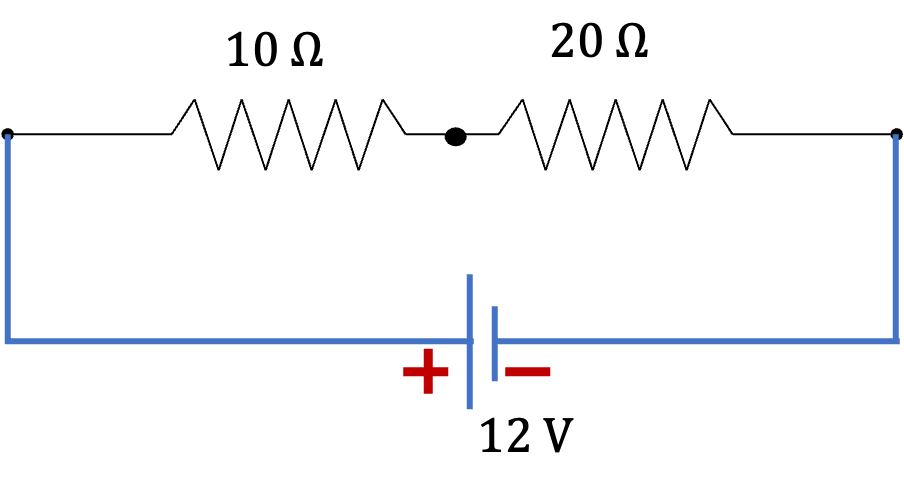
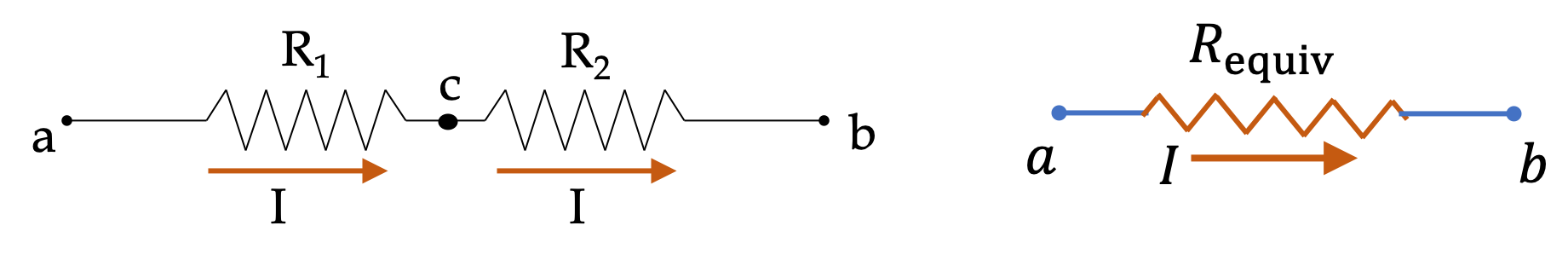Example 34.30. Current, Voltage, and Power in Resistors in Series Circuit.
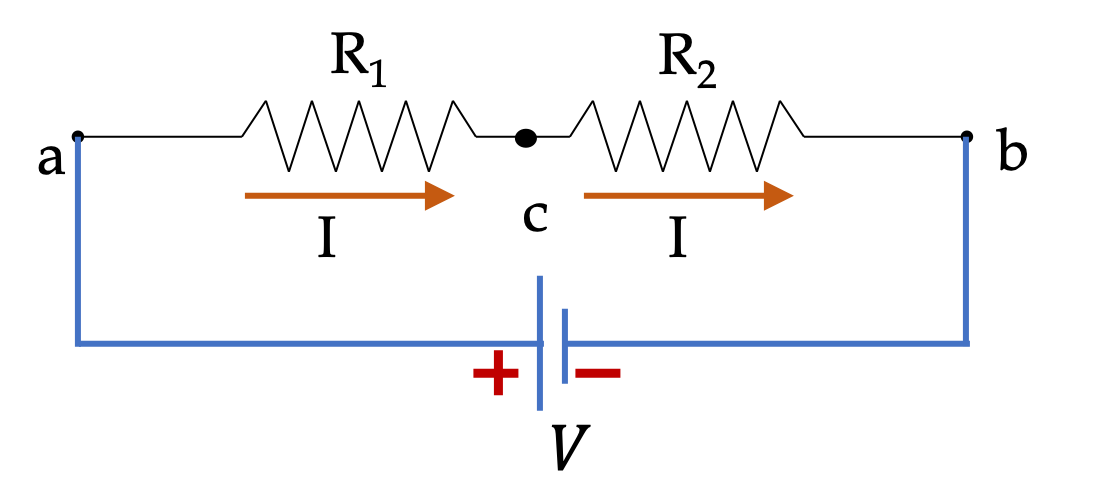
The circuit in Figure 34.31 shows two resitors in series with a voltage source.
(a) Find current through each resitor, (b) Find voltage across each resitor, (c) Find power dissipated in each resistor, (d) How much energy is delivered to the circuit by the voltage source in \(10\text{ minutes}\text{.}\)
Answer.
(a) \(0.4\text{ A}\text{,}\) (b) \(4\text{ V}\text{,}\) \(8\text{ V}\text{,}\) (c) \(1.6\text{ W} \text{,}\) \(3.2\text{ W} \text{,}\) (d) \(2,880\text{ J} \text{.}\)
Solution 1. (a)
Since the resitors are in series, same current \(I\) flows through both resitors and encounters a net resistance \(R_1 + R_2\text{.}\)
\begin{align*}
I \amp = \dfrac{V}{R_1 + R_2} = \dfrac{12\ \text{V}} {10\ \Omega + 20\ \Omega} = 0.4\text{ A}.
\end{align*}
Solution 2. (b)
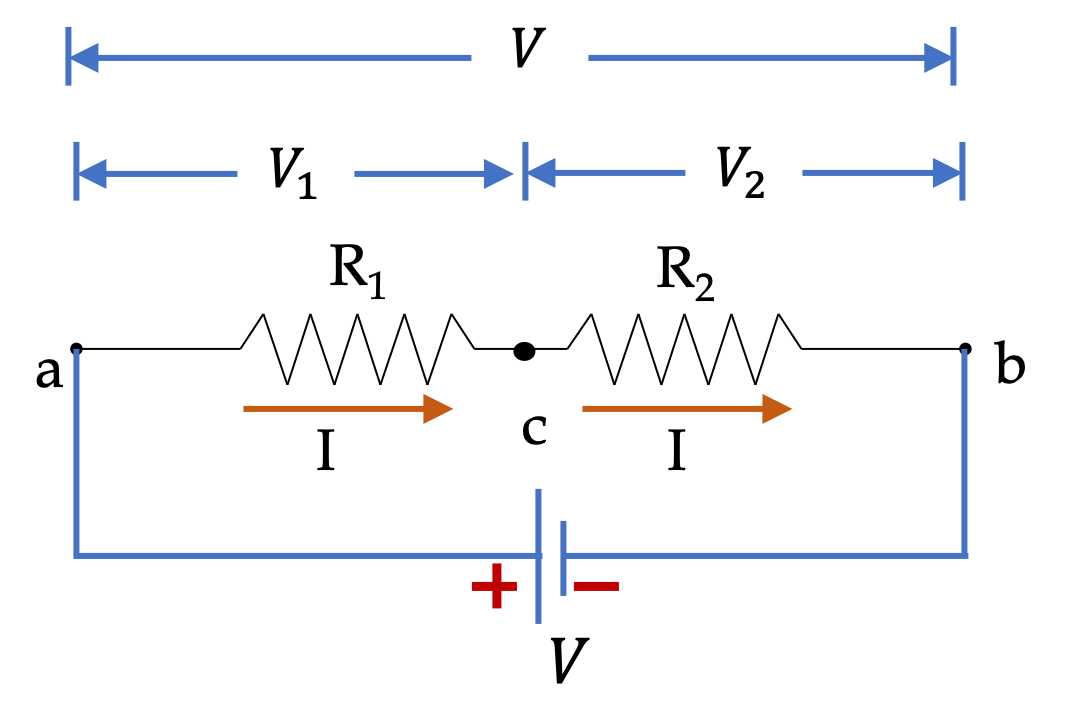
Same current \(I\) flows through both resitors. Applying Ohm’s law on each resitor will give us the potential drops across each of the resitors.
\begin{align*}
V_1 \amp = I_1R_1 = IR_1 = 0.4\text{ A} \times 10\ \Omega = 4\text{ V},\\
V_2 \amp = I_2R_2 = IR_2 = 0.4\text{ A} \times 20\ \Omega = 8\text{ V}.
\end{align*}
Solution 3. (c)
Power dissipated in a resitor equals \(IV\) for that resistor.
\begin{align*}
P_1 \amp = I_1 V_1 = I V_1 = 0.4\text{ A} \times 4\text{ V} = 1.6\text{ W}.\\
P_2 \amp = I_2 V_2 = I V_1 = 0.4\text{ A} \times 8\text{ V} = 3.2\text{ W}.
\end{align*}
Solution 4. (d)
Energy conservation means the energy lost to the resitors must be suplied by the voltage source. Therefore, the net power of the source must be
\begin{equation*}
P_\text{source} = P_1 + P_2 = 4.8\text{ W}.
\end{equation*}
Therefore energy supplied in \(10\text{ minutes}\) will be
\begin{equation*}
E = P_\text{source}\Delta t = 4.8\text{ W} \times 600\text{ s} = 2,880\text{ J}.
\end{equation*}