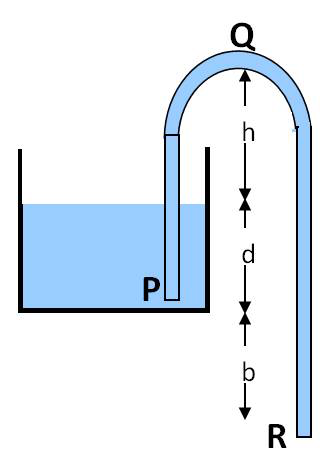
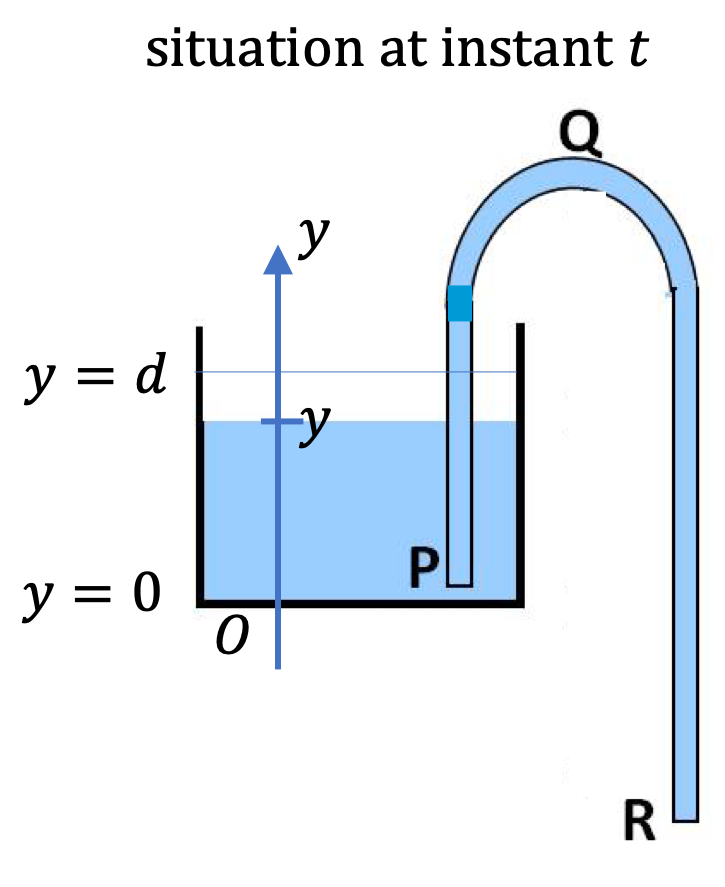
To minitor the progress of emptying of the tank, we use a \(y\)-coordinate of the top of the water at instant \(t\) with initial value \(y=0\text{.}\) This gives the velocity at the top, to be denoted by \(v\text{,}\) which is a function of time \(t\text{.}\)
\begin{equation*}
v = -\dfrac{dy}{dt},
\end{equation*}
where minus is because the layer is moving down while positive \(y\) axis is pointed up.
The Bernouli equation for the flow through the entire siphon will be
\begin{equation}
p_{\text{atm}} + \dfrac{1}{2} \rho v^2 + \rho g (b + y) = p_{\text{atm}} + \dfrac{1}{2} \rho v_R^2. \tag{18.45}
\end{equation}
Let \(v_R\) denote the speed with which fluid comes out at bottom. The conservation of volume gives
\begin{equation*}
A_0 v = A v_R.
\end{equation*}
Putting this in the Eq.
(18.45) yields
\begin{equation*}
v = \sqrt{\dfrac{2g(b+y)}{a^2-1}},\ \ \ (a \ne 1)
\end{equation*}
where \(a = A_0/A\text{.}\) Replacing \(v\) by \(-dy/dt\) this eqution becomes a differential equation.
\begin{equation*}
-\dfrac{dy}{dt}= \sqrt{\dfrac{2g(b+y)}{a^2-1}},
\end{equation*}
We can write this in a way that allows integrating easier.
\begin{equation}
\dfrac{dy}{ \sqrt{ b + y} } = - \sqrt{\dfrac{2g }{a^2-1}} dt.\tag{18.46}
\end{equation}
Integrating this equation from \(y=d\) to \(y=0\) corresponding to \(t=0\) to \(t=T\text{,}\) the time to drain gives us the following result.
\begin{equation*}
2\sqrt{b+d} - 2\sqrt{b} = \left[ \sqrt{\dfrac{2g }{a^2-1}}\right]\ T.
\end{equation*}
Therefore,
\begin{equation*}
T = \dfrac{\sqrt{2}}{\sqrt{g}}\sqrt{ a^2-1 } \left( \sqrt{b+d} - \sqrt{b}\right).
\end{equation*}