Linear Dielectrics

Section 33.5 Linear Dielectrics

Subsection 33.5.1 Polarization

Most chemicals have either polarized bonds and hence carry permanent dipoles throughout the sample, or the bonds can be polarized by placing a sample in an electric field. We call these materials dielectrics. Plastic, glass, water, ceramic, etc., are examples of dielectrics.

Normally, the permanent microscopic dipoles have random orientations, which makes their electrical influence negligible. However, if they are aligned, for instance, in the presence of external electric field, the electric fields of individual dipoles will tend to add up. Aligned microscopic dipoles usually have strong influence on the electric field inside them and in their neighborhod.

To describe electrical properties of a dielectric, it is useful to introduce a quantity called polarization which is the dipole moment per unit volume at a particular place. We denote individual dipole moment vector by small letter \(\vec p\) and polarization by \(\vec P\text{.}\) Suppose we have \(N\) dipoles in a volume \(V\text{,}\) then polarization will be

\begin{equation*} \vec P = \dfrac{1}{V}\sum_{i=1}^{N}\, \vec p_i \end{equation*}

If microscopic dipoles are randomly oriented, then their vector sum will end up being zero. This is what happens in liquid water, whose molecules are oriented in random directions. Even though, each molecule of water is poalrized, the bulk water is not polarized. To polarize bulk water requires external electric field. When we place a water sample in an external elctric field, say in the space between two oppositely charged metals, water molecules will rotate and preferentially align with the external field, resulting in a net polarization of the material. Some crystals are naturally polarized.

Subsection 33.5.2 Electric Field Inside a Dielectric

Suppose you place a piece of mica between two oppositely charged plates. This will polarize mica. As a result, in addition to the original electric field of the charges on the plates, there will be electric fields of the aligned dipoles of mica.

Inside mica, the electric field of the dipoles are in the opposite direction to the external field; therefore, the net field is less than what used to be when mica was not there. That is, the net effect of aligned dipole moments is to reduce the electric field inside a dielectric. This effect is called electric field screening.

Figure 33.19. Electric field is screened inside a dielectric. Net electric field lines between plates charged by placing \(\pm Q\) on the plates when: (a) vacuum between parallel plates, (b) dielectric between parallel plates of dielectric constant \(\epsilon_r = 2\text{,}\) and (c) dielectric between parallel plates of dielectric constant \(\epsilon_r = 3\text{.}\) Note, less lines per unit area shown when weaker field.

The fraction by which electric field inside a dielectric drops is called dielectric constant of the material, to be denoted by \(\epsilon_r\text{.}\) Suppose \(E_0\) denote the electric field at a place when there is no dielectric there, and \(E_\text{net}\) the field at the same location inside a dielectric placed there, then dielectric constant is defined by

\begin{equation} E_\text{net} = \dfrac{E_0}{\epsilon_r}.\tag{33.11} \end{equation}

We call \(E_0\) the external electric field while \(E_\text{net}\) is the actual electric field. Dielectric constant is also known as relative permittivity since it equals the ratio of electric permittivity (\(\epsilon\)) of the material and the electric permittivity (\(\epsilon_0\)) of vacuum.

\begin{equation*} \epsilon_r = \frac{\epsilon}{\epsilon_0}. \end{equation*}

Table 33.20 gives dielectric constants of a number of materials of practical use.

Table 33.20. Dielectric constants at \(20^\circ\text{C}\) (Kaye-Laby Online, 2005)


Material	Dielectric constant \(\epsilon_r\)	Material	Dielectric constant \(\epsilon_r\)
SOLIDS
Cellophane	7.0	Pyrex Glass	4.7
Epoxy Resin	3.6	Quartz	4.3
Mica	7.0	Teflon	2.1
Mylar (polyester)	3.25
Paper	3.7	LIQUIDS
Polycarbonate	2.8	Castor oil	4.5
Polypropylene	2.2	Water	80.4
Polystyrene	2.6	GASES
Porcelain	5.5	Air (1 atm.)	1.00054

Subsection 33.5.3 Electric Field Inside a Dielectric

Electric field inside a dielectric placed in an external electric field \(\vec E_\text{ext}\) consists of two parts: the external E field and an electric field by the dipoles as quantified by the polarization of the dielectric, \(\vec P\text{.}\) Let us denote the net field inside a dielectric by \(\vec E_\text{net}\) and that by polarization by \(E_\text{pol}\text{.}\) Then,

\begin{equation} \vec E_\text{net} = \vec E_\text{ext} + \vec E_\text{pol}.\tag{33.12} \end{equation}

Electric field due to polarization is a difficult quantity to compute since polarization itself depends on the net electric field. Clearly, \(\vec E_\text{pol}\) is opposite to \(\vec E_\text{ext}\) and depends on magnitude of net field \(E_\text{net}\) acting on the dipoles. Therefore, it is reasonable to expect that \(E_\text{pol}\) be directly proportional to \(E_\text{net}\)

\begin{equation} \vec E_\text{pol} = - \chi_e\,\vec E_\text{net}.\tag{33.13} \end{equation}

The proportionality constant \(\chi_e\) is called electric susceptibility. This will give us

\begin{equation*} \vec E_\text{net} = \dfrac{1}{1+\chi_e}\vec E_\text{ext}, \end{equation*}

which, when compared to Eq. (33.11) gives the following relation between dielectric constant \(\epsilon_r\) and electric susceptibility, \(\chi_e\text{.}\)

\begin{equation} \epsilon_r = 1 + \chi_e.\tag{33.14} \end{equation}

Subsection 33.5.4 Linear Dielectrics

Experimentally, we find that, if the applied electric field is not too great, the degree of polarization varies linearly with the net field. We use this observation to define material’s electric susceptibility by the following relation.

\begin{equation} \vec P = \epsilon_0 \chi_e \vec E_\text{net} = \left( \epsilon_0 - \epsilon_0 \epsilon_r\right) \vec E_\text{net} .\tag{33.15} \end{equation}

A material that obeys this linear relation between polarization and net electric field is called a linear dielectric.

The product of dielectric constant and permittivity of vacuum, i.e., \(\epsilon_r\epsilon_0\text{,}\) is called the permittivity of the dielectric, just as \(\epsilon_0\) is called the permittivity of vacuum or free space. Permittivity is denoted by the same symbol \(\epsilon\) without the subscript zero.

\begin{equation} \epsilon = \epsilon_0\, \epsilon_r.\tag{33.16} \end{equation}

You can read this definition as saying that dielectric constant is permittivity of the medium relative to the permittivity of vacuum.

In addition to the linear dielectrics, there are special materials, called ferroelectrics, such as Barium Titanate (\(\text{BaTiO}_3\)), that do not respond to an external electric field in the manner outlined above. Their polarizations are not linear in the electric field. Furthermore, while the polarization in linear dielectrics go to zero due to thermal randomization of the dipoles when the external electric field is removed, the dipoles in the ferroelectrics remain aligned even when the external electric field is removed as long as the temperature is lower than a critical value called Curie point.

Subsection 33.5.5 Dielectric Breakdown

If the electric field at a point is so great that electrons can be ripped off from the molecules, a dielectric breakdown of the medium occurs. The loose electrons accelerate and strike other molecules with great energy and cause more electrons to come off molecules leading to an avalanche of moving electrons and ions.

This is responsible for the lightning shown in Figure 33.21. Usually it takes considerable electric field to reach the dielectric breakdown level. For instance, you need approximately \(3\text{ MV/m}\) of electric field to cause the electric breakdown of the dry air; polycarbonate, a very commonly used insulating material, has a dielectric strength of approximately \(300\text{ MV/m}\text{.}\)

Figure 33.21. Lightning as an example of dielectric breakdown ( Credits: NOAA Photo Library, NOAA Central Library; OAR/ERL/National Severe Storms Laboratory (NSSL), Photographer C. Clark)

Exercises 33.5.6 Exercises

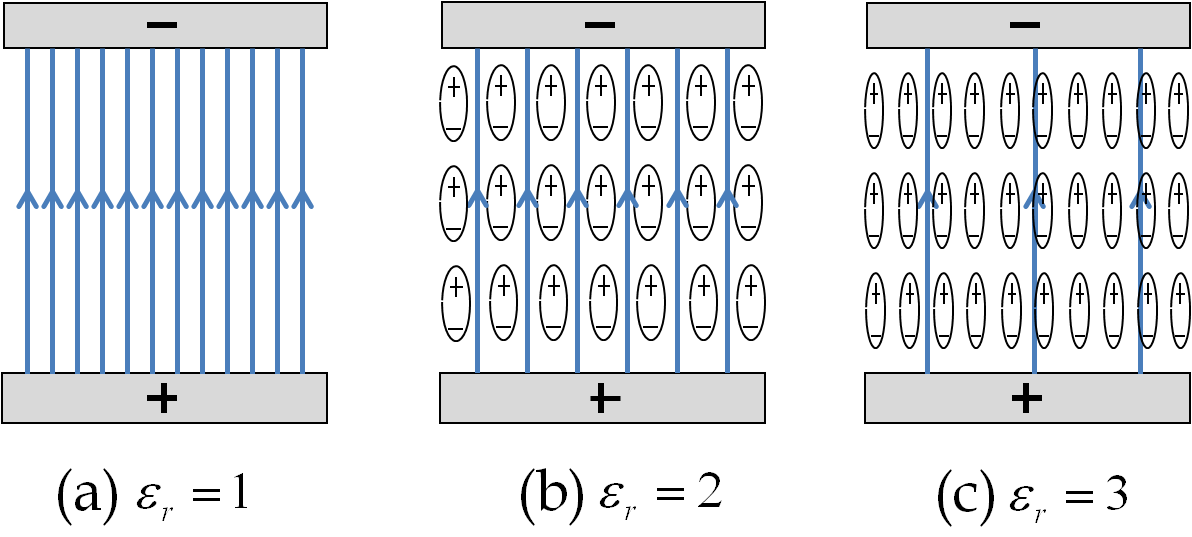
1. Electric Field in Paper Between Two Charged Paper Plates.

Two pieces of aluminum foil of dimensions \(25\text{ cm} \times 25 \text{ cm}\) is separated by a piece of paper of thickness \(0.2\) mm. The foils are oppositely charged with \(\pm 50\ \mu\text{C}\text{.}\)

(a) What is the electric field in the paper?

(b) What is the polarization of paper?

Data: \(\epsilon_{r,\text{ paper}} = 3.7\text{.}\)

Hint.

(a) Use \(E=E_0/\epsilon_r\text{.}\) (b) Use definition.

Answer.

(a) \(2.44\times 10^{7}\text{ N/C}\text{,}\) (b) \(5.83\times 10^{-4}\ \textrm{C/m}^2\)

Solution 1. (a)

Electric field in a dielectric is related to electric field in the absence of the dielectric by

\begin{equation*} E = \dfrac{E_0}{\epsilon_r}. \end{equation*}

In the space between two oppositely charged parallel plates with nothing between the plates.

\begin{equation*} E_0 = \dfrac{Q/A}{\epsilon_0}. \end{equation*}

Therefore,

\begin{equation*} E = \dfrac{Q/A}{\epsilon_0\epsilon_r}. \end{equation*}

Putting in numerical values we get

\begin{align*} E \amp = \dfrac{ 50\times 10^{-6} }{ 8.85\times 10^{-12}\,\times 3.7\times 0.25^2 }\\ \amp = 2.44\times 10^{7}\text{ N/C}. \end{align*}

Solution 2. (b)

Polarization of the paper depends on the electric field in the paper found in (a).

\begin{equation*} P = \epsilon_0(\epsilon_r - 1)E. \end{equation*}

Putting in numerical values we get

\begin{align*} P \amp = 8.85\times 10^{-12} \times (3.7-1) \times 2.44\times 10^{7}\\ \amp = 5.83\times 10^{-4}\text{ C/m}^2. \end{align*}

2. Polarization of Plastic Wrapped Around a Charge Steel Sphere.

A steel ball of radius 2 cm is charged with \(-10\ \mu\)C. The charged steel ball is surrounded by plastic spherical shell of thickness \(3\) cm. (a) Find electric field at a point in the plastic at a distance \(4\) cm from the center of the ball. (b) Find the polarization of the plastic.

Data: \(\epsilon_{r,\text{ plastic}} = 2.8\text{.}\)

Hint.

Use relation between electric field when no dielectric and that in the presence.

Answer.

(a) \(2\times 10^{13}\ \textrm{N/C}\text{,}\) (b) \(320\ \textrm{C/m}^2\text{.}\)

Solution 1. a

We can find the electric field at 4 cm when there is no plastic by using the result for spherical symmetry when applying Gauss’s law. Thus, magnitude of electric field at distance \(r \gt 2\text{ cm}\) is

\begin{align*} E_0 \amp = \dfrac{1}{4\pi\epsilon_0}\: \frac{q_{\textrm{tot}}}{r^2} \\ \amp = 9\times 10^9\times \dfrac{10^{-5}}{0.04^2} = 5.6\times 10^{13}\:\textrm{N/C}. \end{align*}

With plastic in the space around the sphere in place of vacuum, the electric field will be reduced by a factor of the dielectric constant \(\epsilon_r\text{.}\)

\begin{align*} E \amp = \dfrac{E_0}{\epsilon_r} \\ \amp = \dfrac{5.6\times 10^{13}\:\textrm{N/C}}{2.8} = 2\times 10^{13}\:\textrm{N/C}. \end{align*}

Solution 2. b

The magnitude \(P\) of the polarization is related to the magnitude of the electric field \(E\) as follows.

\begin{align*} P \amp = \epsilon_0\:(\epsilon_r-1)\:E\\ \amp = 8.85\times 10^{-12}\times (2.8-1)\times 2\times 10^{13} = 320\:\textrm{C/m}^2. \end{align*}

3. Electric Field and Polarization of Two Different Layers of Dielectrics Filling Space Between Parallel Plates.

The space between two charged aluminum foils, \(15\text{ cm}\times 15\text{ cm}\text{,}\) separated by \(2\text{ mm}\) is filled with \(1\text{ mm}\) thick mica and \(1\text{ mm}\) paper. The foils are oppositely charged with charges \(\pm 10\ \mu\text{C}\text{.}\)

(a) Find the electric field in mica and in paper.

(b) Find the polarization of mica and paper.

Data: \(\epsilon_{r,\text{ mica}} = 7\text{,}\) \(\epsilon_{r,\text{ paper}} = 3.7\text{.}\)

Hint.

Use the electric field when there is no dielectric to find the field.

Answer.

\(E_{\textrm{mica}} = 7.14\times 10^6\:\textrm{N/C} \text{,}\) \(E_{\textrm{paper}} = 1.35\times 10^7\:\textrm{N/C}\text{,}\) \(P_{\textrm{mica}} = 3.8\times 10^{-4}\:\text{C/m}^2\text{,}\) \(P_\text{paper} = 4.5\times 10^{-4}\:\text{C/m}^2\text{.}\)

Solution 1. (a)

Let us find the electric field when there is no dielectric first. For two oppositely charged plates with nothing between the plates, the electric field in the space between the plates will have the following magnitude,

\begin{equation*} E_0 = \dfrac{Q}{\epsilon_0 A} = 5\times 10^7\:\textrm{N/C}. \end{equation*}

Therefore, the electric field in the mica and paper will be reduced by the corresponding dielectric constant,

\begin{align*} E_{\textrm{mica}} \amp = \dfrac{E_0}{\epsilon_{r,\text{ mica}}}\\ \amp = \dfrac{5\times 10^7\:\textrm{N/C}}{7} = 7.14\times 10^6\:\textrm{N/C}\\ E_{\textrm{paper}} \amp = \dfrac{E_0}{\epsilon_{r,\textrm{ paper}}} \\ \amp = \dfrac{5\times 10^7\:\textrm{N/C}}{3.7} = 1.35\times 10^7\:\textrm{N/C} \end{align*}

Solution 2. (b)

We can find the polarization of the two dielectrics, from field in them and their dielectric constant.

\begin{align*} P_{\textrm{mica}} \amp = \epsilon_0\:(\epsilon_{r,\text{ mica}} - 1)\:E_{\text{mica}} \\ \amp = 8.85\times 10^{-12}\times (7-1)\times 7.14\times 10^6 = 3.8\times 10^{-4}\:\text{C/m}^2. \end{align*}

We don’t have to start over to get the polarization of paper. In the present example, we can do the following.

\begin{align*} P_\text{paper} \amp = \dfrac{\epsilon_{r, \text{paper}}}{ 1- \epsilon_{r, \text{paper}}} \times \dfrac{ 1- \epsilon_{r, \text{mica}}}{\epsilon_{r, \text{mica}}}\times P_\text{mica}\\ \amp = \dfrac{3.7}{3.7-1}\times \dfrac{7-1}{7}\times 3.8\times 10^{-4}\:\text{C/m}^2.\\ \amp = 4.5\times 10^{-4}\:\text{C/m}^2. \end{align*}

Prev Top Next