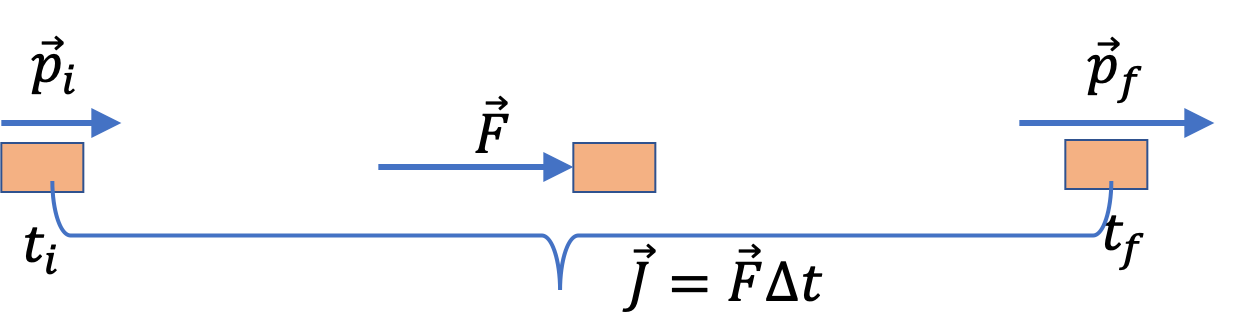
Speed is the magnitude of velocity, which can be obtained by dividing the magnitude of momentum by mass. In general, to find the final momentum, we just add the change in momentum to the initial momentum.
\begin{equation}
\vec p_f = \vec p_i + \Delta \vec p,\tag{7.21}
\end{equation}
in which we can replace \(\Delta \vec p \) by impulse. We now compute \(\vec J\) to find \(\vec p_f\) from \(\vec p_i\) and \(\vec J\text{.}\)
Suppose the direction of the force does not change during the time the golf club was in contact with the ball and let that direction be the positive \(x \) axis. Then, we can just work with the \(x \) components.
\begin{equation*}
J_x = 4,600\text{ N} \times 0.5\text{ ms} = 2.3\text{ N.s}.
\end{equation*}
This is equal to the change in momentum of the ball.
\begin{equation*}
\Delta p_x = 2.3\text{ N.s} = 2.3\text{ kg.m/s}.
\end{equation*}
The
\(x \) component of Eq.
(7.21) gives the final momentum
\begin{equation*}
p_{f,x} = p_{i,x} + \Delta p_x = 0 + 2.3\text{ kg.m/s}.
\end{equation*}
Dividing by mass we get the \(x\) component of the velocity.
\begin{equation*}
v_x = \dfrac{2.3\text{ kg.m/s}}{0.046\text{ kg}} = 50\text{ m/s}.
\end{equation*}
Speed is the absolute value, which is the same, \(50\text{ m/s}\text{.}\)
Note: Working with components here is an overkill, but if we are not thinking the vector aspects of our equations, we will run into trouble in any non-trivial situation, e.g., the same problem with a baseball, in which baseball has a non-zero initial velocity, which is in the opposite direction to the final.