Section 36.2 Magnetic Dipole Field
The magnetic field of a current in a circular loop given in Eq. (36.9) has interesting limiting behaviors. We will now show that for microscopic loops, magnetic field varies as inverse cube of the distance from the loop. This is similar to the way electric field of an electric dipole varies. Therefore, we will interpret this type of magnetic field as magnetic field of an ideal magnetic dipole, i.e., a microscopic magnet.
To obtain the distance-dependence of a micoscopic loop we look at Eq. (36.9) for \(z \gg R\) and find the leading behavior using Maclauren expansion using variable \(\epsilon = R/z \text{.}\) This will give us magnetic field in direction perpendicular to the loop.
\begin{align*}
B_P \amp = \frac{\mu_0I_R^2}{2} \lim_{z \gg R} \dfrac{1}{\left(R^2 + z^2\right)^{3/2}} = \frac{\mu_0I_R^2}{2z^3} \lim_{\epsilon \ll 0} \dfrac{1}{\left(1 + \epsilon^2\right)^{3/2}}, \\
\amp = \frac{\mu_0I_R^2}{2z^3} \lim_{\epsilon \ll 0} \left[ 1 - \frac{3}{2}\,\epsilon^2 + \cdots\right] = \frac{\mu_0I_R^2}{2} \frac{1}{z^3}.
\end{align*}
Introducing factors of \(\pi\) and rewriting the field in the following way helps with the identification of the magnetic dipole moment of the current loop in the formula, which we will denote by symbol \(\mu\text{,}\) as before. This field is called dipole field and denoted by attaching a subscript to the symbol for the field.
\begin{align*}
B_{\textrm{dipole}} \amp = \frac{\mu_0}{2\pi} \frac{I\pi R^2}{z^3} = \frac{\mu_0}{2\pi} \frac{IA}{z^3} = \frac{\mu_0}{2\pi} \frac{\mu}{z^3}
\end{align*}
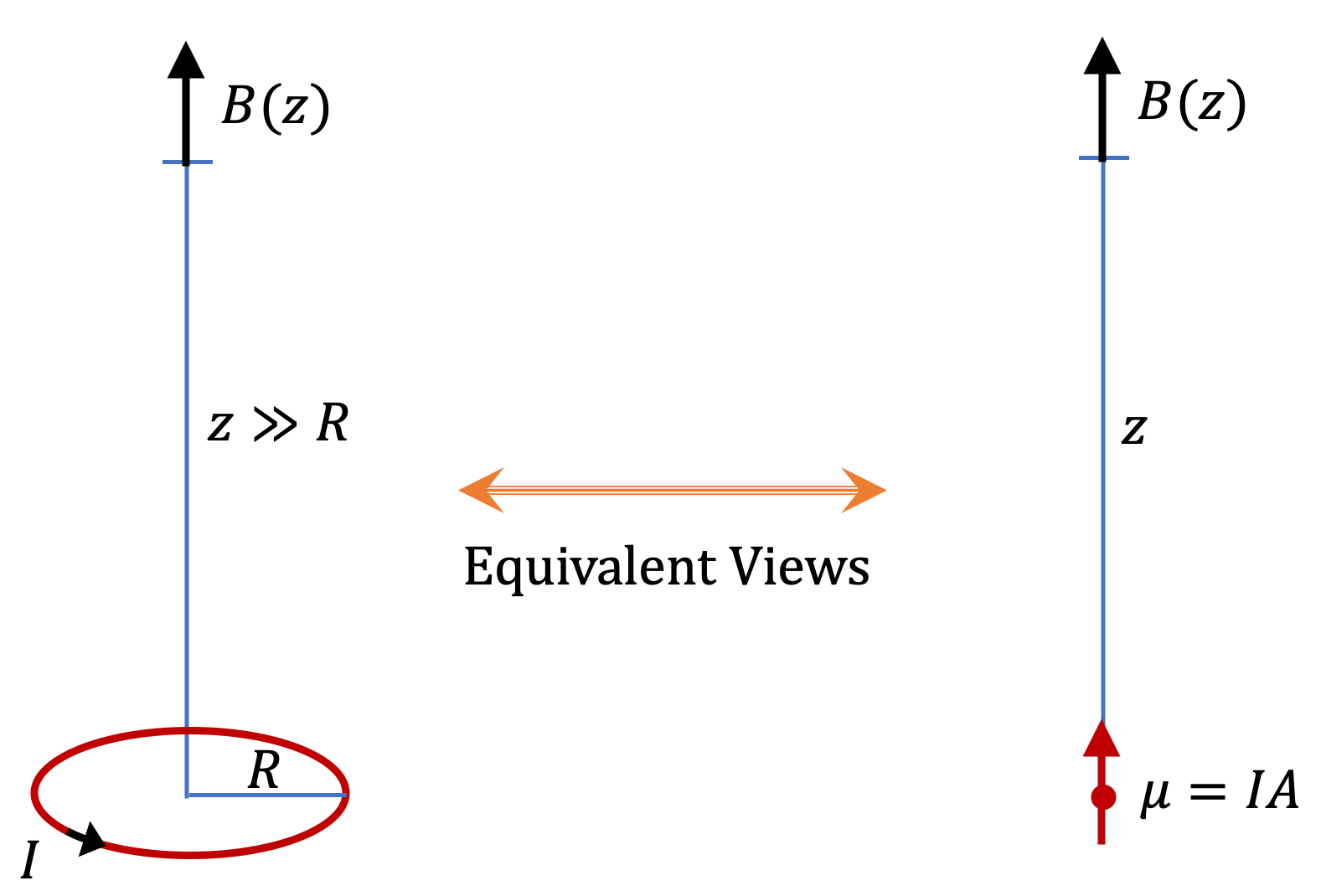
The \(z \gg R\) limit on the field of a current loop provides two views of magnetic phenomenon - as tiny current loops and as magnetic dipole as illustrated in Figure 36.32. Think of the loop as a loop of current or alternately think of the current loop as a magnetic dipole moment of the current loop. Conversely, we can represent a magnetic dipole moment, such as a magnetic dipole moment of a tiny magnet by a current loop where the product of the area of the loop and the current is equal to the magnetic dipole moment.
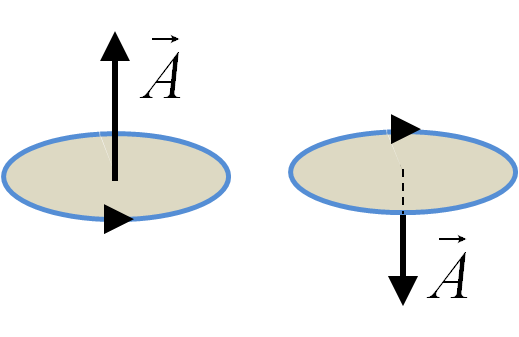
Since current has direction, magnetic dipole moment has direction as well. The vector form of magnetic dipole moment is defined by introducing a quantity called the area vector. The magnitude of the area vector of a planar surface is defined to be equal to the area of the surface, and the direction is along the normal given by the following right-hand rule.
Sweep around the direction of the current with four finger of your right palm, then the direction in which your thumb points is the direction of the area vector. For your reference, area vectors are illustrated in Figure 36.33.
\begin{equation*}
\vec A =
\begin{cases}
\text{Magnitude} = \text{Area}\\
\text{Direction} =\text{Normal to Area};\, \text{Right-Hand Rule}.
\end{cases}
\end{equation*}
With this definition of the area vector, the magnetic dipole moment vector is given as
\begin{equation*}
\vec \mu = I\vec A.
\end{equation*}

