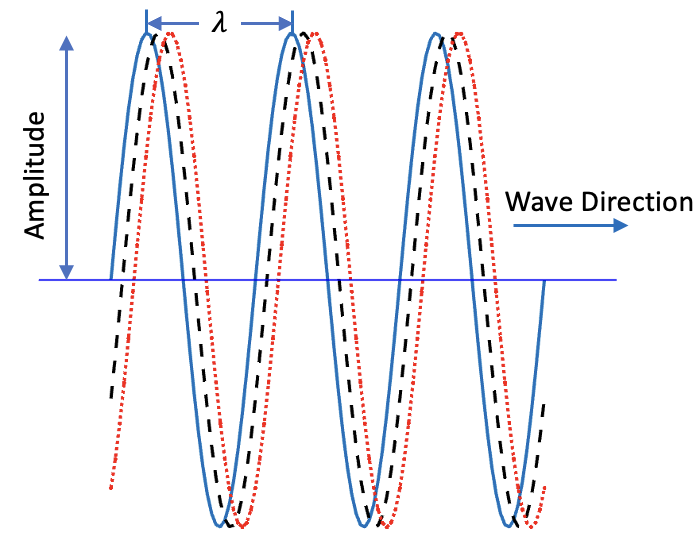
1. Obtaining Properties of Sinusoidal Waves from Wave Function.
The sound produced by a speaker is given by the following pressure difference wave in air.
\begin{equation*}
\Delta p = (10 \text{ Pa})\, \cos(k x + 6000\, t + \pi),
\end{equation*}
where \(x\) is in meters and \(t\) in seconds and \(\Delta p(x,t)\) is the difference in atmospheric pressure from the ambient pressure at location \(x\) at time \(t\text{.}\) Suppose speed of this wave is \(343\text{ m/s}\text{.}\)
(a) What is the amplitude of the wave?
(b) What is the frequency of the wave?
(c) What is the wavelength of the wave?
Hint.
The \(\Delta p\) is just a sinusoidal wave.
Answer.
(a) \(10\text{ Pa}\text{,}\) (b) \(954.9\text{ Hz}\text{,}\) (c) \(35.9\text{ cm}\text{.}\)
Solution 1. a
Here \(\Delta p\) is actually a sinusoidal wave. In the text, we used the symbol \(y\) for the wave, but here, it is \(\Delta p\text{.}\) The amplitude is just the number multiplying the oscillating part.
\begin{equation*}
\text{Amplitude} = 10\text{ Pa}.
\end{equation*}
Solution 2. b
We can read of angular frequency \(\omega\) from the number that multiplies \(t\) in the argument of coine, and then obtained frequency \(f\) from it.
\begin{equation*}
f = \frac{\omega}{2\pi} = \frac{6000}{2\pi} = 954.9\text{ Hz}.
\end{equation*}
I have used \(\text{Hz}\) for the unit since it is regular cycle per second, and not the angular cycle.
Solution 3. c
If we knew the wavenumber \(k\text{,}\) we will get \(\lambda\) from it. But, since we don’t know \(k\) yet, but we do know \(v\) and \(f\text{,}\) therefore, we will use the fundamental equation.
\begin{equation*}
\lambda = \frac{v}{f} = \frac{343}{954.9} = 0.359\text{ m} = 35.9\text{ cm}.
\end{equation*}