Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 39.5 Inductance Bootcamp

Exercises Exercises

Mutual Inductance

1. Mutual Inductance of a Solenoid Surrounded by a Loop.
Follow the link: Example 39.3.
2. Mutual Inductance of a Loop of Wire and a Solenoid.
Follow the link: Example 39.11.
3. Mutual Inductance of Two Circular Loops with a Common Center.
Follow the link: Example 39.8.
4. Mutual Inductance of two Solenoids, One Inside the Other.
Follow the link: Example 39.10.

Self-Inductance

6. (Calculus) Self Inductance of a Coaxial Cable.
Follow the link: Example 39.15.
7. (Calculus) Self-inducatance of a Rectangular Torroid.
Follow the link: Example 39.16.

Inductance in Circuits

8. Time Constant of an \(RL\) Circuit.
Follow the link: Example 39.21.
9. Power Dissipation in an \(RL\) Circuit.
Follow the link: Example 39.22.
10. Variation of Current in an RL-Circuit.
Follow the link: Example 39.27.
13. ( Calculus) Numerical Study of Current Rise and Magnetic Energy Storage in a Coil.
Follow the link: Exercise 39.3.4.3.
14. (Calculus) Voltage Drop Across a Coil with Changing Current.
Follow the link: Exercise 39.3.4.4.
15. (Calculus) Different Time Constants in Different Branches of an RL-Circuit.
Follow the link: Exercise 39.3.4.5.

Miscellaneous

16. (Calculus) Mutual Inductance of a Straight Wire and a Square Loop and Magnetic Energy.
(a) Determine the mutual inductance of a long wire and a square loop of side a lying in the same plane with a separation \(d\) as shown in Figure 39.35. (b) Determine the amount of magnetic energy stored in the area of the square loop when a steady current \(I\) flows in the straight wire.
Figure 39.35.
Answer.
(a) \(\mathcal{M} = \frac{\mu_0 a}{2\pi}\ln{\left( \frac{d+a}{d}\right)}\text{.}\)
Solution 1. (a)
(a) For the purpose of calculations, we let a current \(I\) pass through the long straight wire and find the flux of magnetic field of this current through the square loop. The flux divided by the current will give us the mutual inductance of the two circuits. The magnetic field of the current in the wire at a point P inside the loop which is at a distance \(r\) from the wire has the magnitude
\begin{equation*} B_{\text{of wire}} = \dfrac{\mu_0\:I}{2\pi\:r}, \end{equation*}
direction perpendicular to the plane surface of the loop. Consider a strip of are of width \(dr\) and height \(a\) at a distance \(r\) away from the wire. The flux through this strip will be
\begin{equation*} d\Phi = \dfrac{\mu_0\:I}{2\pi\:r}\:a\:dr \end{equation*}
Therefore, the flux through the area of the loop will be
\begin{equation*} \Phi_{\text{through loop}} = \dfrac{\mu_0\:I\:a}{2\pi } \int_{d}^{d+a}\:\dfrac{dr}{r} = \dfrac{\mu_0\:I\:a}{2\pi } \:\ln\left( \dfrac{d+a}{d}\right). \end{equation*}
Dividing this by \(I\) will give the mutual inductance of the two circuits.
\begin{equation*} \mathcal{M} = \dfrac{\mu_0\:a}{2\pi } \:\ln\left( \dfrac{d+a}{d}\right) \end{equation*}
Solution 2. (b)
(b) The energy stored in the magnetic field in the area enclosed by the loop can be calculated by imagining a volume about the loop. Suppose the given loop is in the \(xy\)-plane. Then we imagine an infinitesimal height \(\Delta z\) perpendicular to the loop. The energy in the magnetic field in a small box of length \(a\text{,}\) width \(dr\text{,}\) and height \(\Delta z\) located at a distance \(r\) from the axis and parallel to the axis is given by the product of the square of the average magnitude of the magnetic field in the box and the volume of the box.
\begin{equation*} dU =\dfrac{1}{2\mu_0} B^2 \times a\times dr\times \Delta z = \dfrac{1}{2\mu_0}\: \left( \dfrac{\mu_0\:I}{2\pi\:r} \right)^2\times a\times dr\times \Delta z. \end{equation*}
We need to add up energy in all such boxed in the space of the loop. This yields the following integral.
\begin{equation*} U = \dfrac{\mu_0\:I\:a\Delta z}{8\pi^2} \int_{d}^{d+a}\: \dfrac{dr}{r^2} = \dfrac{\mu_0\:I\:a\Delta z}{8\pi^2}\:\left( \dfrac{1}{d} - \dfrac{1}{d+a}\right). \end{equation*}
Note the magnetic energy depends on the height of the box whose one edge is the square loop in the problem. We can compute the energy per unit of the height of the box by dividing \(U\) by \(\Delta z\text{.}\)
17. (Calculus) Self Inductance of a Coaxial Cable.
(a) Determine the self-inductance per unit length of a coaxial cable with an inner hollow conductor of radius \(a\) and outer conductor of radius \(b\text{.}\) (b) Find the amount of energy in magnetic field stored per unit length of the coaxial cable if a current \(I\) flows in the inner wire and returns in the outer conductor. (Ignore the effect of the magnetism of the material.)
Hint.
Try passing current \(I\) through the central wire with the return current in the outer jacket.l
Answer.
(a) \(\dfrac{\mu_0}{2\pi}\:\ln\left( \dfrac{b}{a}\right)\text{,}\) (b) \(U/h = \frac{\mu_0 I }{4\pi}\left( 1/a-1/b\right)\text{.}\)
Solution 1. (a)
(a) For the purpose of calculations, we pass a current I through the coaxial cable with the return current in the outer jacket. The magnetic field between the conductors is circulating with magnitude given by Ampere’s law.
\begin{equation*} B = \dfrac{\mu_0}{2\pi}\:\dfrac{I}{r}\ \ (a \lt r \lt b). \end{equation*}
Let us find the flux through a rectangular cross-section of height H parallel to the length of the cable and width from \(r = a\) to \(r = b\text{.}\)
\begin{align*} \Phi \amp = \iint\:\vec B\cdot d\vec A = \dfrac{\mu_0\: I\: h}{2\pi}\:\int_a^b\:\dfrac{dr}{r}\\ \amp = \dfrac{\mu_0\: I\: h}{2\pi}\:\ln\left( \dfrac{b}{a}\right). \end{align*}
Dividing the flux \(\Phi\) by the current \(I\) give the self-inductance the cable, from which we obtain the self-inductance per unit length to be
\begin{equation*} \dfrac{L}{h} = \dfrac{\Phi/I}{h} = \dfrac{\mu_0}{2\pi}\:\ln\left( \dfrac{b}{a}\right) \end{equation*}
Solution 2. (b)
(b) The amount of magnetic energy can be obtained by integrating \(B^2\) in the volume between the conductors. We take a length \(h\) parallel to the wires to do the calculation. The energy stored in this finite space would be
\begin{align*} U_{\text{mag}}\amp = \dfrac{1}{2\mu_0}\:\int\:B^2\:dV\\ \amp = \dfrac{1}{2\mu_0}\:\int\:\left(\dfrac{\mu_0}{2\pi}\:\dfrac{I}{r} \right)^2 \:2\pi\:h\:dr\\ \amp = \dfrac{\mu_0\:I^2\:h}{4\pi}\:\left(\dfrac{1}{a} -\dfrac{1}{b} \right). \end{align*}
Hence, magnetic energy per unit length is
\begin{equation*} \dfrac{U_{\text{mag}}}{h} = \dfrac{\mu_0\:I^2}{4\pi}\:\left(\dfrac{1}{a} -\dfrac{1}{b} \right). \end{equation*}
18. (Calculus) Self-inducatance of a Rectangular Torroid and Magnetic Energy in Torroid.
(a) Find the self-inductance of a loop of wire with \(N\) turns around a rectangular cross-section torroid of internal radius \(a\text{,}\) external radius \(b\) and height \(h\text{.}\) (b) Find the amount of energy in the magnetic field if a current \(I\) runs in the wire.
Hint.
Use Ampere’s law to find magnetic field at a point inside the torroid. You will find that magnetic field depends on the radial distance from the axis.
Answer.
(a) \(L = \left(\mu_0Nh/2\pi \right)\ln{\left( b/a\right)}\text{,}\) (b) \(\dfrac{\mu_0\:N\: I^2\: h}{4\pi}\:\ln\left( \dfrac{b}{a}\right) \text{.}\)
Solution 1. (a)
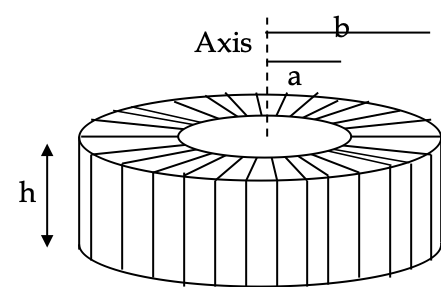
(a) From symmetry in the situation we expect the magnetic field inside the solenoid to circulate about the axis. Consider a circular Amperian loop of radius \(r\) around the axis with \(a\lt r\lt b\text{.}\) Then, from Ampere’s law we will have
\begin{equation*} 2\pi\;r\:B = \mu_0\:N\:I, \end{equation*}
since \(N\) currents will pass through the are of the Amperian loop. This shows that the magnetic field inside the solenoid is not constant but depends on the distance \(r\) from the axis.
\begin{equation*} B = \dfrac{\mu_0\:N\:I}{2\pi}\:\dfrac{1}{r}.\ \ \ \ (1) \end{equation*}
This is different from what you know for a straight solenoid, where the magnetic field is constant in the space of the solenoid. The flux through the cross-section of the present solenoid can be obtained by integrating the magnetic field in (1) over the area of cross-section of the toroid.
\begin{align*} \Phi \amp = \int_a^b\: \dfrac{\mu_0\:N\:I}{2\pi}\:\dfrac{1}{r}\times h\: dr\\ \amp = \dfrac{\mu_0\:N\:I\: h}{2\pi}\:\ln\left( \dfrac{b}{a}\right). \end{align*}
Factoring out current gives the self-inductance \(L\) of the toroid.
\begin{equation*} L = \dfrac{\Phi}{L} = \dfrac{\mu_0\:N\: h}{2\pi}\:\ln\left( \dfrac{b}{a}\right) \end{equation*}
Solution 2. (b)
(b) When a current \(I\) passes through a circuit of self-inductance \(L\text{,}\) the total magnetic energy can be shown to be equal to \(\dfrac{1}{2} L I^2\text{.}\) Therefore,
\begin{equation*} U_{\text{mag}} = \dfrac{\mu_0\:N\: I^2\: h}{4\pi}\:\ln\left( \dfrac{b}{a}\right). \end{equation*}
You can obtain this result by also integrating \((B^2/2\mu_0)dV\) over the volume of the toroid.
PrevTopNext
Found typo?