Magnetic Flux

Section 38.2 Magnetic Flux

Before we look more closely upon Faraday’s law, let us study magnetic flux, which will be used to state the law. Similar to the electric field flux, magnetic flux through a surface is a measure of number magnetic field lines that pass through that surface. You may recall from your study of electric flux that relative orientation of the surface and direction of the field is important for flux. For instance, if a field is parallel to a surface, there will be no flux, and if a field is perpendicular to the surface, it will have maximum flux as shown in Figure 38.5. At other angles, the flux will be in-between.

Figure 38.5. Magnetic flux through a surface is largest when the surface is perpendicular to the magnetic field lines. In general, magnetic flux of a uniform magnetic field through flat surface of a loop is \(\Phi_B = BA\cos\theta\text{.}\) We write this in vector notation as \(\Phi_B = \vec B\cdot \vec A\text{.}\)

We denote magnetic flux of magnetic field \(\vec B\) by \(\Phi_B\text{.}\) Consider a open flat surface with area \(A\text{.}\) To take orientation of the surface, we introduce area vector \(\vec A\) which has magnitude \(A\) and direction normal to the surface.

1. Uniform Field Case.

If \(\vec B\) is uniform, then flux of this field through the surface will be

\begin{align} \Phi_{B,\text{uniform}} \amp = \vec B \cdot \vec A.\tag{38.1}\\ \amp = B A \cos\,\theta,\notag \end{align}

where \(\theta\) is angle between \(\vec B\) and \(\vec A\text{.}\)

2. (Calculus) General Case.

In the general case of arbitrary field and arbitrary surface, we break the surface into small patches of flat areas, and apply Eq. (38.1) to each patch. Summing over all patches gives us an estimate of the net flux through the surface. We can write this process as a formal sum.

\begin{equation} \Phi_B \approx \sum_\text{patches} \vec B \cdot \Delta \vec A.\tag{38.2} \end{equation}

In the limit of infinitesimally small patches, we get the exact flux, which we write as a conceptual integral.

\begin{equation} \Phi_B = \int_\text{surface}\, \vec B \cdot d \vec A.\tag{38.3} \end{equation}

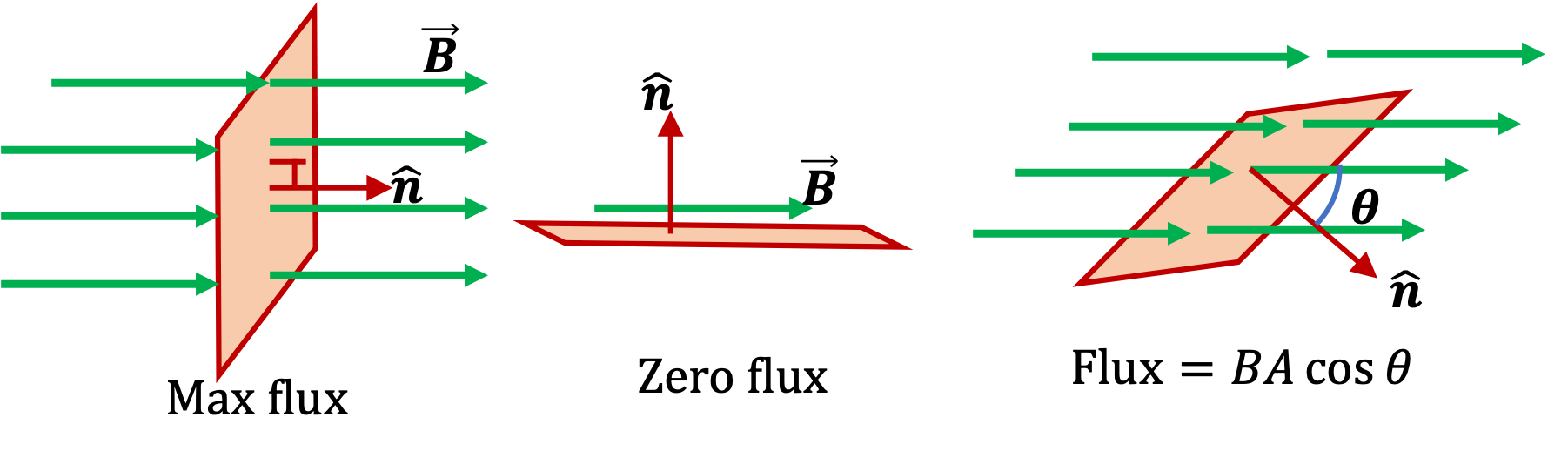
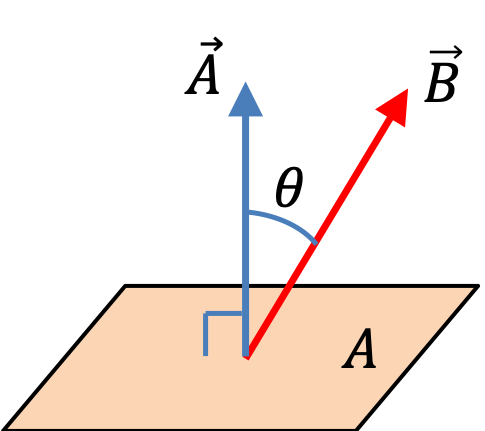
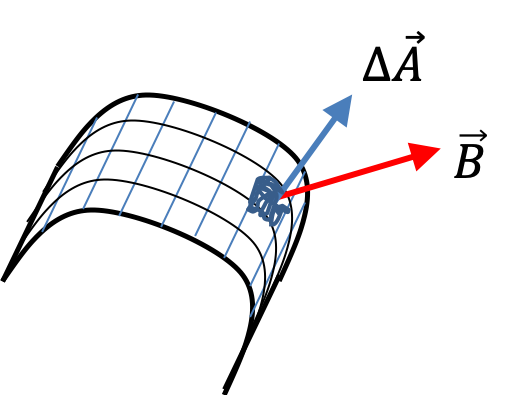
Example 38.6. Flux of Constant Magnetic Field - Simple Surfaces.

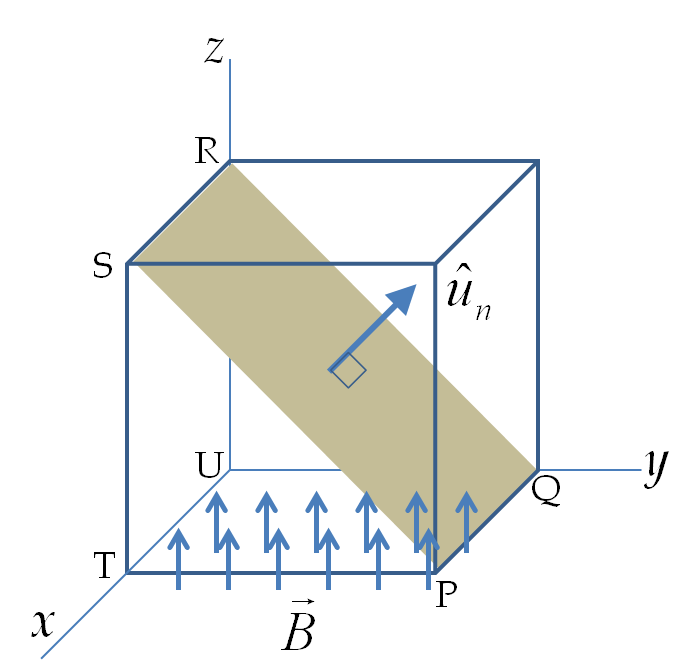
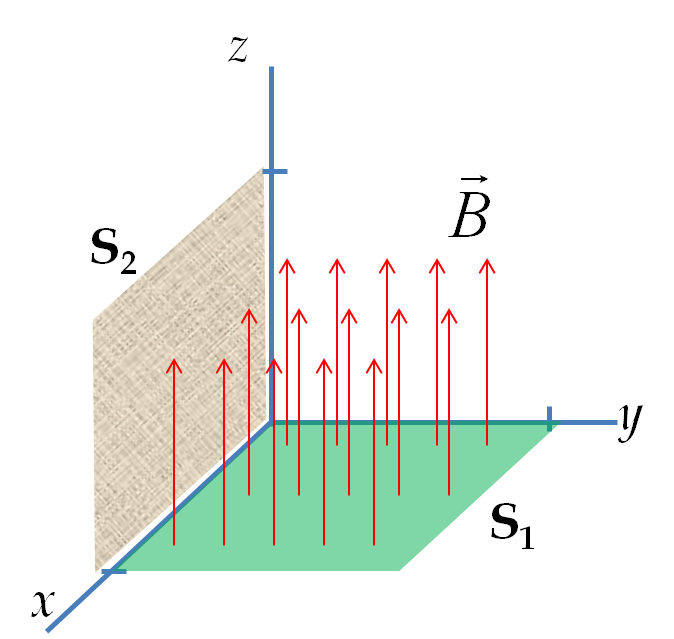
A constant magnetic field \(B_0\hat u_z \) is present in a region as shown in Figure 38.7. Calculate magnetic flux through two flat surfaces of area \(A\) (a) in the \(xy\)-plane (surface \(S_1\)) and (b) in the \(xz\)-plane (surface \(S_2\)).

Answer.

(a) \(\pm B_0 A\text{,}\) (b) \(0\text{.}\)

Solution 1. a

The given magnetic field is pointed towards positive \(z\) axis. The normal to an area in the \(xy\)-plane is along the \(z\) axis. The unit vector normal to the \(xy\)-plane will be either \(+\hat u_z \) or \(-\hat u_z \text{,}\) which we can write as \(\pm\hat u_z \text{.}\) The magnetic flux is

\begin{align*} \Phi_B \amp = \left( B_0\hat u_z \right) \cdot \left(\pm \hat u_z A\right)\\ \amp =\pm B_0 A. \end{align*}

Solution 2. b

The normal to the area in the \(xz\)-plane is \(\pm\hat u_y\text{.}\) The dot product between the magnetic field and the normal now equals zero. Therefore, the flux of the magnetic field pointed towards the positive \(z\) axis through an area in the \(xz\)-plane will be zero. A similar argument will show that the flux of the given magnetic field through an area in the \(yz\)-plane will also be zero.

Example 38.8. Flux of Constant Magnetic Field - Slanted Surface.

Given a constant magnetic field of magnitude \(B_0\) in the positive \(z\)-axis direction find the magnetic flux through the rectangular surface PQRS inside the cube of side \(a\) as shown in Figure 38.9, where \(\hat u_n\) is normal to the surface.

Answer.

\(B_0\, a^2\text{.}\)

Solution.

Recall that a dot product also has a meaning in terms of the projection of vectors. For instance, \(\vec B\cdot\vec A\) is equal to the product of the magnitude \(|\vec B|\) and the projection of the vector \(\vec A\) in the the direction of the vector \(\vec B\text{.}\)

Here, the projection of the area denoted in the figure as PQRS in the direction of magnetic field is equal to the area at the base, viz. PQUT through which magnetic field lines pass perpendicularly. Therefore, the flux through PQRS is equal to the flux through PQUT.

\begin{equation*} \Phi_B = B_0\, a^2. \end{equation*}

Example 38.10. (Calculus) Flux of Inhomogeneous Magnetic Field.

Magnetic field of a current in a wire is inhomogeneous and varies over space. In the Cartesian coordinate system shown in Figure 38.11, the magnetic field of the current \(I\) towards the positive \(z\)-axis in a long straight wire is given by

\begin{equation*} \vec B = \dfrac{\alpha}{x^2+y^2}\left(- y\hat u_x + x \hat u_y\right), \end{equation*}

where \(\alpha = \mu_0 I/2\pi\text{.}\) The magnetic field lines in teh figure are shown circulating about \(z\) axis.

Find the flux through surfaces (a) \(S_1\text{,}\) (b) \(S_2\text{,}\) and (c) \(S_3\) shown in Figure 38.11.

Answer.

(a) \(0\text{,}\) (b) \(\mp\alpha \left(c_2-c_1 \right) \ln{\left(\dfrac{b_2}{b_1}\right)} \text{,}\) (c) \(\pm\alpha \left(c_2-c_1 \right) \ln{\left(\dfrac{a_2}{a_1}\right)}\text{.}\)

Solution 1. a

Since the magnetic field varies over an area, we will think in terms of area element \(dA\) of each surface.

The normal \(\hat u_n\) to surface \(S_1\) is along the \(z\)-axis. Therefore, the dot product of \(\vec B\) with \(\hat u_n\) will vanish, which makes the flux through \(S_1\) zero.

Solution 2. b

The normal \(\hat u_n\) to surface \(S_2\) along the \(x\)-axis, giving \(\hat u_n = + \hat u_x\) or \(\hat u_n = - \hat u_x\text{.}\) Due to this ambguity in normal direction, we will get two answers. The area element on \(S_2\) in the \(yz\)-plane is

\begin{equation*} d\vec A = \pm dydz \hat u_x. \end{equation*}

The surface \(S_2\) has \(x=0\text{.}\) The magnetic flux through \(S_2\) will be given by the following integral based on the general formula.

\begin{align*} \Phi_B \amp = \iint \vec B\cdot d\vec A\\ \amp = \mp\alpha\int_{y=b_1}^{y=b_2}\int_{z=c_1}^{z=c_2}\left[ \dfrac{y}{x^2+y^2}\right] _{x=0}dydz\\ \amp = \mp\alpha \left(c_2-c_1 \right) \ln{\left(\dfrac{b_2}{b_1}\right)} \end{align*}

Solution 3. c

A similar calculation as part (b) will give the following two answers for the magnetic flux through \(S_3\text{.}\)

\begin{equation*} \Phi_B = \pm\alpha \left(c_2-c_1 \right) \ln{\left(\dfrac{a_2}{a_1}\right)} \end{equation*}

Prev Top Next