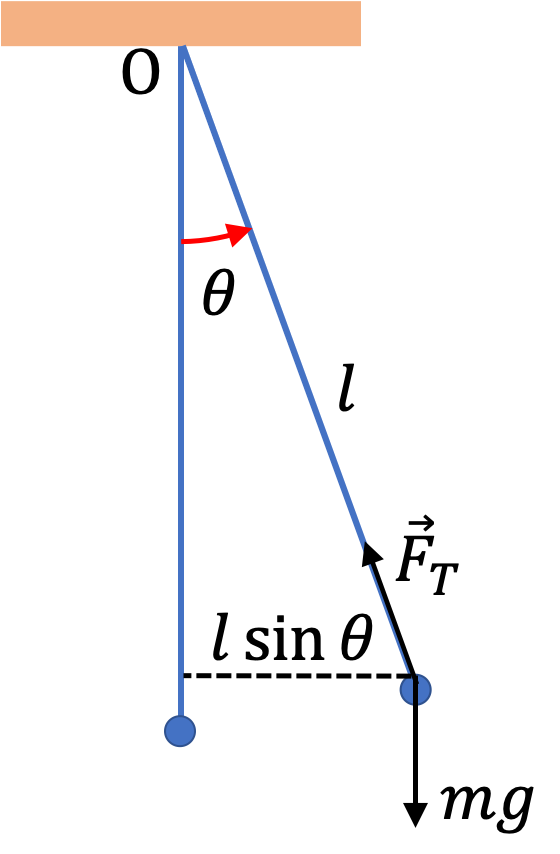
1. Period of a Child on a Swing.
(a) A child is swinging on a swing such that her center of mass is \(2.0\text{ m}\) from the suspension point. How long does she take to complete one swing?
(b) The child moves to another swing and finds that her swings now take \(1.2\) times as much. What is the distance of her center of mass now in this swing?
Hint.
(a) Treat swing as a plane pendulum. (b) Use \(T \propto \sqrt {L}\text{.}\)
Answer.
(a) \(2.84\text{ sec}\text{,}\) (b) \(2.88\text{ m}\text{.}\)
Solution.
(a) Treating the child as a point mass at her center of mass, the swing is just a plane pendulum. Then, the time to complete one swing is the period of the pendulum.
\begin{equation*}
T = 2\pi\,\sqrt{ \dfrac{L}{g} } = 2\pi\,\sqrt{ \dfrac{2}{9.81} } = 2.84\text{ sec}.
\end{equation*}
(b) Since only length is different, we can use the proportionality, \(T \propto \sqrt {L}\text{,}\) to deduce
\begin{equation*}
\dfrac{T_2}{T_1} = \sqrt{{L_2}{L_1}}.
\end{equation*}
Therefore, \(L_2/L_1\) is square of the ratio of times. This gives
\begin{equation*}
L_2 = 1.2^2\times 2.0\text{ m}= 2.88\text{ m}.
\end{equation*}
Note that length is not \(1.2\times\text{.}\) If that was the case, the answer would have been \(2.4\text{ m}\text{,}\) but the actual answer is \(2.88\text{ m}\text{.}\)