Magnetic Dipoles

Section 37.1 Magnetic Dipoles

All magnets have North and South poles. Even the tiniest of magnets, an electron also has North and South poles. Thus, fundamentally, a magnet consits of dipoles and the fundamental property of interest is the magnetic dipole moment, denoted as \(\vec \mu\text{.}\)

Previously we have discussed two ways of looking at magnetic dipoles illustrated in Figure 37.1: (1) as a tiny magnet and (2) a tiny current loop. Tiny current loop with current \(I\) and area \(A\) is a dipole because its magnetic field has the \(1/r^3\) behavior expected of a dipole field for a dipole moment equal to \(IA\text{.}\)

Figure 37.1. A current loop with \(IA=\mu\) is equivalent to a magnet of dipole moment \(\mu\text{.}\)

When we represent a magnetic dipole by a fictitious current loop, the current in the model loop is called bound current to distinguish them from current flowing in a conductor, which is called free current. Bound current model of magnetic dipole helps with calculations involving magnets.

In the following subsections, we will work out force and torques on magnetic dipoles using the current loop model.

Subsection 37.1.1 Force on a Magnetic Dipole in a Uniform Magnetic Field

We wish to find magnetic force on a magnetic dipole as shown in Figure 37.2(a). First we replace magnetic dipole by a square loop of current, as shown in (b) of the figure, and find magnetic force on that equivalent current loop.

Figure 37.2. Force on a dipole in a uniform magnetic field: (a) the original problem, (b) equivalent problem, where magnetic dipole moment is replaced by a square current loop. We find magnetic force on each side and then add them vectorially.

By using the force law for current in uniform magnetic field

\begin{equation*} \vec F = I \vec L \times \vec B, \end{equation*}

it is easy to show that forces on the opposite sides are equal in magnitude and opposite in direction. Hence,

\begin{align*} \amp \vec F_\text{qr} + \vec F_\text{sp} = 0,\\ \amp \vec F_\text{pq} + \vec F_\text{rs} = 0. \end{align*}

Therefore,

\begin{equation*} \vec F_\text{current loop} = 0. \end{equation*}

From this result we can deduce the answer to the original problem by taking the following special type of limits.

\begin{equation*} A\rightarrow 0\text{ and } I\rightarrow\infty\text{ keeping the product } IA \text{ fixed.} \end{equation*}

Clearly, taking these limits does not change the result of zero net force. Hence, we conclude that the magnetic force on the dipole in a uniform magnetic field is zero.

\begin{equation*} F_\text{dip} = 0. \text{ (uniform magnetic field)} \end{equation*}

Subsection 37.1.2 Torque on a Magnetic Dipole in a Uniform Magnetic Field

Even though the net force on a magnetic dipole in a uniform magnetic field is zero, the torque on the dipole is not zero if magnetic dipole moment is pointed at an angle to the magnetic field as in Figure 37.2 as we will show now.

We will find torque of these force about axis through the center of the loop and perpendicular to the direction of the magnetic field as shown in Figure 37.3.

Let \(\theta\) be the angle between the magnetic dipole moment vector \(\vec \mu\) and external magnetic field \(\vec B\) as in Figure 37.3(a), which would mean normal to the equivalent square loop, pqrsp, will make this angle with magnetic field.

Figure 37.3. Torque on a dipole in a uniform magnetic field is computed by torque of forces on the equivalent current loop. The axis is perpendicular to the direction of \(\vec B\) and passes through the center of the square loop of side \(a\text{.}\) The torques of \(\vec F_\text{qr}\) and \(\vec F_\text{sp}\) are both zero. The torques of \(\vec F_\text{pq}\) and \(\vec F_\text{rs}\) are nonzero and can be computed from the figure on the right. The magnitude of net torque equald \(\tau = I a^2 B \sin\,\theta = \mu B \sin\,\theta\text{.}\)

Since lines of forces \(\vec F_\text{qr}\) and \(\vec F_\text{sp}\) pass through the axis, their lever arms are zero; hence, their torques about this axis are zeros.

To find the torques from \(\vec F_\text{pq}\) and \(\vec F_\text{rs}\text{,}\) it is helpful to draw another figure from the perspective of looking down the axis. With \(a\) the length of a side of the square loop, we get lever arm for these forces to be \(\dfrac{a}{2}\sin\,\theta\text{.}\) The two forces have the same magnitude \(IaB\text{.}\) Their directions are also same, which is into the page. Therefore net torque on the equivalnet current loop is

\begin{equation*} \tau = 2IaB\times \dfrac{a}{2}\sin\,\theta = Ia^2 B \sin\,\theta, \end{equation*}

in the direction into the page, i.e., towards the negative \(z\) axis. Here area of the loope is \(A = a^2\text{.}\) Writing torque in the vector notations, we get the \(z\) component of torque to be

\begin{equation} \vec \tau = -\hat u_z \, IA B \sin\,\theta.\tag{37.1} \end{equation}

From this result we can deduce the answer to the original problem by taking the following special type of limits.

\begin{equation*} A\rightarrow 0\text{ and } I\rightarrow\infty\text{ keeping the product } IA \text{ fixed.} \end{equation*}

It is readily seen that as soon as we replace \(IA\) by \(\mu\text{,}\) the limit is trivial and gives us the following for torque on the original dipole.

\begin{equation*} \vec \tau_\text{dip} = -\hat u_z \, \mu B \sin\,\theta. \end{equation*}

We can write this in terms of vectors \(\vec \mu\) and \(\vec B\text{.}\)

\begin{equation} \vec \tau_\text{dip} = \vec \mu \times \vec B.\tag{37.2} \end{equation}

Subsection 37.1.3 (Calculus) Force on a Magnetic Dipole in a Nonuniform Magnetic Field

Consider a magnetic dipole in a nonuniform magnetic field. Rather than do the most general case, let the direction of the external magnetic field be fixed in the positive \(y\) direction with magnitude varying only as a function of \(x\) as indicated in Figure 37.4

\begin{equation*} \vec B = \hat u_y \, B(x). \end{equation*}

Figure 37.4. Force on a dipole in a uniform magnetic field: (a) the original problem, (b) equivalent problem, where magnetic dipole moment is replaced by a square current loop. We find magnetic force on each side and then add them vectorially.

Now, we see that forces along \(x\) axis, viz., \(\vec F_\text{qr}\) and \(\vec F_\text{sp}\text{,}\) cancel.

\begin{equation*} \vec F_\text{qr} + \vec F_\text{sp} = 0, \end{equation*}

but forces in the \(x\) axis, viz., \(\vec F_\text{pq}\) and \(\vec F_\text{rs}\text{,}\) do not cancel due to different values of magnetic field at the two sides. The resulting \(x\) component of the net force on the equivalnet current loop is

\begin{align*} F_x \amp = F_\text{pq,x} + F_\text{rs,x},\\ \amp = Ia B_\text{pq} - Ia B_\text{rs},\\ \amp = Ia \left( B_\text{pq} - B_\text{rs}\right),\\ \amp = Ia \times \left( x_\text{pq} - x_\text{rs}\right) \times \left( \dfrac{B_\text{pq} - B_\text{rs}}{ x_\text{pq} - x_\text{rs}}\right),\\ \amp = Ia \times \left( a\,\cos\,\theta\right) \dfrac{\Delta B}{\Delta x}. \end{align*}

Taking \(\Delta x \rightarrow 0\) and replacing \(Ia^2\) by \(\mu\) we get

\begin{align*} F_x \amp = \mu\,\cos\,\theta\, \dfrac{\partial B}{\partial x},\\ \amp = \mu_y \dfrac{\partial B_y}{\partial x} = \dfrac{\partial }{\partial x} \left( \mu_y B_y \right) \end{align*}

A more general analysis gives the following formula.

\begin{equation} \vec F = \vec\nabla\left( \vec \mu \cdot \vec B \right),\tag{37.3} \end{equation}

where \(\vec \nabla\) is

\begin{equation*} \vec \nabla = \hat u_x \, \dfrac{\partial}{\partial x} + \hat u_y \, \dfrac{\partial}{\partial y} + \hat u_z \, \dfrac{\partial}{\partial z}. \end{equation*}

Subsection 37.1.4 Energy of a Magnetic Dipole in External Field

The potential energy of a dipole \(\vec \mu\) in an external magnetic field \(\vec B\) depends upon its orientation with respect to the field. When the dipole makes an angle \(\theta\) with respect to the field, potential energy is given by

\begin{equation*} U = -\mu\,B\,\cos\,\theta = -\vec \mu \cdot \vec B, \end{equation*}

with zero reference when they are perpendicular, i.e., when \(\theta=90^\circ\text{.}\)

This says that the potential energy is minimum when the dipole is parallel to the field and maximum when antiparallel. We can deduce this result by using Calculus as I show next.

(Calculus) Derivation of Potential Energy. Since magnetic force is a conservative force, we expect magnetic force \(\vec F\) to be related to a potential energy function \(U\) by the gradient.

\begin{equation*} \vec F = -\vec \nabla U. \end{equation*}

Now, using Eq. (37.3), we find the the potential energy of a dipole in an external field is

\begin{equation} U = - \vec \mu \cdot \vec B,\tag{37.4} \end{equation}

where zero of potential energy is when the dipole is pependicular to the field.

Exercises 37.1.5 Exercises

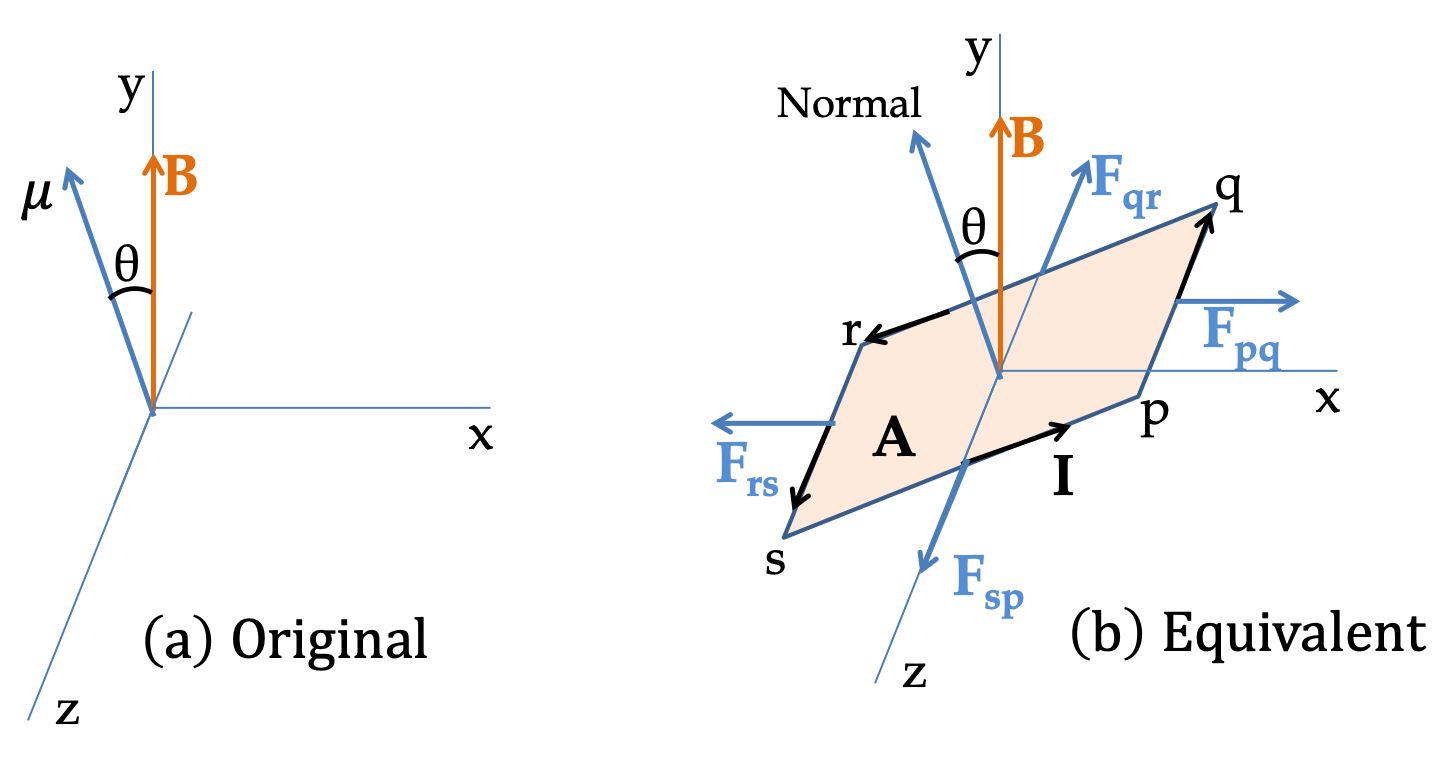
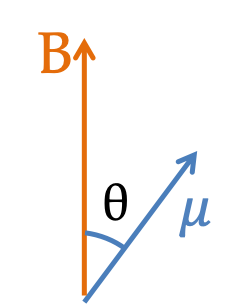
1. Magnetic Moment of an Orbitting Electron.

An electron moves in a circular orbit of radius \(0.05\text{ nm}\) with speed \(1.0\times 10^{5}\text{ m/s}\text{.}\) What is its magnetic dipole moment. Assume the motion of electron is fast enough to constitute a steady current.

Hint.

Electron will pass any point in the circle once in one period of the circular motion. Use this to find current and then multiply by the area.

Answer.

\(4.0\times 10^{-25}\, \text{A.m}^2\)

Solution.

Assuming motion of the electron as charge continuously moving in a circle, we find current by noting that one unit of electron’s charge moves past a point in one period.

\begin{equation*} I = \dfrac{\Delta q}{\Delta t} = \dfrac{e}{T}, \end{equation*}

with \(T\) being the time for an electron to complete one cycle.

\begin{equation*} T = \dfrac{2\pi R}{v} = \dfrac{2\pi \times 0.05\text{ nm}}{1.0\times 10^{5}\text{ m/s}} = 3.14\times 10^{-15}\text{ s}. \end{equation*}

Therefore,

\begin{equation*} I = \dfrac{1.6\times 10^{-19}\text{ C}}{ 3.14\times 10^{-15}\text{ s} } = 5.1\times 10^{-5}\text{ A}. \end{equation*}

Now, we can get the magnetic dipole moment by multiplying this with the area of the loop.

\begin{align*} \mu \amp = I A = 5.1\times 10^{-5}\text{ A} \times \pi \times (0.05\times 10^{-9}\text{ m})^2 \\ \amp = 4.0\times 10^{-25}\, A.m^2. \end{align*}

2. Rotating a Nuclear Magnetic Dipole in a Magnetic Field.

In a nuclear magnetic resonance (NMR) experiment, a nuclear magnetic dipole is first aligned with a static external magnetic field. Then a dynamic magnetic field of an electromagnetic radiation is applied on the sample to flip the orientation of the dipole to face opposite to the direction of the static field. Suppose it takes \(4.35 \times 10^{-7} \text{ eV}\) of energy to flip the magnetic dipole of a proton when aligned to a magnetic field of magnitude \(2.5\text{ T}\text{.}\) Find the magnetic dipole moment of a proton.

Units: \(1\text{ eV} = 1.6\times 10^{-19}\text{ J}\text{.}\)

Hint.

Find the change in energy.

Answer.

\(1.4\times 10^{-26}\text{ Tm}^2\text{.}\)

Solution.

The energy of magnetic dipole is given by \(U= - \vec\mu \cdot \vec B\text{.}\) Therefore, to flip the direction, from being parallel to \(\vec B\) to antiparall will cost

\begin{equation*} \Delta U = U_f - U_i = \mu B - (- \mu B) = 2\mu B. \end{equation*}

Using numerical values given

\begin{equation*} \mu = \dfrac{\Delta U}{2B} = \dfrac{4.35 \times 10^{-7} \text{ eV} \times 1.6\times 10^{-19}\text{ J/eV}}{2.5\text{ T}} = 1.4\times 10^{-26}\text{ Tm}^2, \end{equation*}

where I wrote the final units by using \(\text{current}\times\text{area}\) equivalence of \(\mu\text{.}\)

3. Torque on a Magnetic Dipole and Energy Required to Flip its Orientation.

A magnetic dipole of magnitude \(9.27 \times 10^{-24}\text{ A.m}^2\) is placed in a magnetic field of magnitude \(3\text{ T}\text{.}\) The dipole makes an angle of \(30^{\circ}\) with the magnetic field. Determine (a) the torque on the dipole and (b) the energy to flip the direction of the dipole by \(180^{\circ}\text{.}\)

Hint.

Use definitions.

Answer.

(a) \(1.39\times 10^{-23}\:\text{N.m} \text{,}\) (b) \(4.82\times 10^{-23}\:\text{J}\text{.}\)

Solution 1. (a)

(a) The magnitude of the torque on a magnetic dipole moment \(\vec \mu\) in a magnetic field \(\vec B\) is given by

\begin{align*} \tau \amp = |\vec \mu\times \vec B| = \mu\:B\:\sin\:\theta \\ \amp = 9.27 \times 10^{-24}\: \text{A.m}^2\times 3\: \text{T}\times \sin\:30^{\circ}\\ \amp = 1.39\times 10^{-23}\:\text{N.m}. \end{align*}

Solution 2. (b)

(b) The energy to flip a magnetic dipole moment is given by

\begin{align*} \Delta U \amp = U_f - U_i \\ \amp = -\mu\:B\:\cos\:(30^{\circ}+180^{\circ}) - [-\mu\:B\:\cos\:30^{\circ}]= 2\mu\: B\:\cos\:30^{\circ}\\ \amp = 2\times 9.27 \times 10^{-24}\: \text{A.m}^2\times3\: \text{T}\cos\:30^{\circ} = 4.82\times 10^{-23}\:\text{J}. \end{align*}

4. Magnetic Dipole Moment and Equivalent Circulating Current from Torque.

A dipole experiences a torque of magnitude \(5 \times 10^{-20}\text{ N.m}\) when its is pointed \(90^{\circ}\) to the direction of an external magnetic field of magnitude \(4\text{ T}\text{.}\) (a) Determine the magnitude of magnetic dipole moment. (b) If the dipole was as a result of a circulating current in a loop of radius \(1.0\text{ mm}\text{,}\) what would be the current in the loop?

Hint.

Use definition.

Answer.

(a) \(\mu = 1.25\times 10^{-20}\ \text{A.m}^2\text{,}\) (b) \(I = 4.0\times 10^{-15}\ \text{A}\text{.}\)

Solution 1. (a)

(a) The magnitude of the torque on a dipole is given by \(\tau = |\vec \mu\times \vec B| = \mu\:B\:\sin\:\theta\text{.}\) Therefore, we can deduce the magnetic dipole moment from the given torque as

\begin{equation*} \mu = \dfrac{\tau}{B\:\sin\:\theta} = \dfrac{5 \times 10^{-20}\: \text{N.m}}{ 4\:\text{T}\:\sin\:90^{\circ}} = 1.25 \times 10^{-20}\:\text{A.m}^2. \end{equation*}

Solution 2. (b)

(b) The dipole moment equals the product of current in the loop and the area of the loop. Therefore,

\begin{equation*} \mu = I A \ \ \Longrightarrow\ \ I = \dfrac{\mu}{A} = \dfrac{1.25 \times 10^{-20}\:\text{A.m}^2}{\pi (0.001\:\text{m})^2} = 3.98\times 10^{-15}\:\text{A}. \end{equation*}

5. Force on a Magnetic Dipole in an Nonuniform Magnetic Field of a Bar Magnet.

The magnetic field near a bar magnet is not uniform. A magnet of magnetic dipole moment magnitude \(3 \times 10^{-22}\text{ A.m}^2\) is brought near the end of a bar magnet where the magnetic field component along the dipole’s direction changes at the rate of \(30\text{ T/m}\text{.}\) Determine the force on the dipole.

Hint.

Use definition.

Answer.

\(9.0\times 10^{-21}\ \text{N}\text{.}\)

Solution.

The force on a dipole is equal to the product of dipole moment and the rate of change of the magnetic field over space. The magnitude of the force will be

\begin{equation*} F = 3\times 10^{-22}\:\text{A.m}^2\times 30\:\text{T/m} = 9\times 10^{-21}\:\text{N}. \end{equation*}

6. Energy for Rotating a Magnetic Dipole by an Arbitrary Angle.

Determine the energy needed to flip the dipole of moment \(10^{-3}\text{ A.m}^2\) in a field of \(2\text{ T}\) from being \(160^{\circ}\) direction to the field to \(20^{\circ}\) direction.

Hint.

Use definition.

Answer.

\(-3.8\times 10^{-3}\ \text{J}\text{.}\)

Solution.

This problem uses the dot product nature of energy formula for a dipole.

\begin{equation*} U = -\vec \mu \cdot \vec B. \end{equation*}

Therefore,

\begin{align*} \Delta U \amp = -\mu\:B\:\cos\:\theta_2 + \mu\:B\:\cos\:\theta_1\\ \amp = -2\times 10^{-3}\:( \cos\:20^{\circ} -\cos\:160^{\circ}) = -3.76\:\text{mJ}. \end{align*}

The negative sign means that the dipole will lose the energy in the process.

7. (Calculus) Force on a Magnetic Dipole in a Nonuniform Magnetic Field Given in Analytic Form.

A dipole of moment \(2\text{ A.m}^2\) is pointed in along \(x\) axis direction in a region of space where magnetic field is given as follows:

\begin{equation*} \vec B = \mu_0I_0\left[-\frac{y}{x^2+y^2}\hat u_x + \frac{x}{x^2+y^2}\hat u_y \right], \end{equation*}

where \(x\) and \(y\) are in \(\text{m}\text{.}\) Find the magnetic force on the dipole when \(x=0.3\text{ m}\) and \(y = 0.4\text{ m}\text{.}\)

Hint.

Use definition.

Answer.

\(7.68\text{ N}\text{.}\)

Solution.

We use the full formula for a force on a dipole in an inhomogeneous magnetic field.

\begin{equation*} \vec F = \hat u_x \: \dfrac{\partial}{\partial\:x}\left( \vec \mu\cdot\vec B\right) + \hat u_y \: \dfrac{\partial}{\partial\:y}\left( \vec \mu\cdot\vec B\right) + \hat u_z \: \dfrac{\partial}{\partial\:z}\left( \vec \mu\cdot\vec B\right). \end{equation*}

Since magnetic dipole moment is pointed along the \(x\)-axis, only the first term will be non-zero.

\begin{equation*} \vec F = \hat u_x \: \dfrac{\partial}{\partial\:x}\left( \mu_x\:B_x\right) = \hat u_x \: \mu\:\dfrac{2xy}{(x^2 + y^2)^2}. \end{equation*}

Putting the numerical values given in the problem, we find

\begin{equation*} \vec F = 2 \times\:\dfrac{2\times 0.3\times 0.4}{(0.3^2 + 0.4^2)^2}\:\:\hat u_x = 7.68\:\text{N}\;\hat u_x . \end{equation*}

8. Force and Torque on a Magnetic Dipole Placed in a Solenoid.

A dipole of moment \(3 \times 10^{-10} \text{A.m}^2\) is placed inside a long solenoid of 2000 turns per meter such that dipole is directed perpendicular to the axis of the solenoid. Determine the force and torque on the dipole when a \(8\ A\) current is passed through the solenoid.

Hint.

Use definition.

Answer.

\(|\vec \tau| = 6\times 10^{-12}\ \text{N.m}\text{.}\)

Solution.

The magnetic field inside a cylindrical solenoid is pointed parallel to the axis and has the following magnitude.

\begin{equation*} B = \mu_0\:n\:I = 4\pi\times 10^{-7}\times 2000\times 8 = 0.02\; \text{T}. \end{equation*}

Since the magnetic field is uniform, there will be no net force on the dipole. Even though there would be no net force on the dipole, there may be a torque on the dipole since the dipole is neither parallel nor antiparallel to the magnetic field. The magnitude of torque is given by

\begin{equation*} \tau = \mu\:B\:\sin\:\theta = 3 \times 10^{-10}\: \text{A.m}^2\times 0.02\: \text{T}\times 1= 6\times 10^{-12}\:\text{Nm}. \end{equation*}

The direction of the torque is perpendicular to both \(\vec \mu\) and \(\vec B\text{.}\) It is given by the right-hand rule applied to the cross-product \(\vec \mu\times \vec B\text{.}\)

Prev Top Next