Example 9.7. Quantifying Rotation of a Disk.
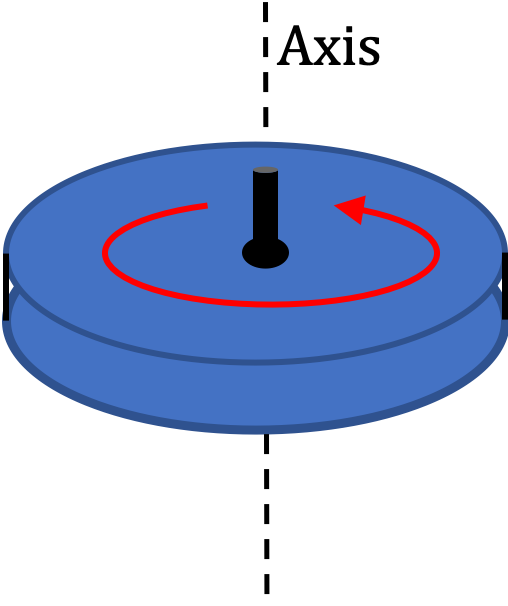
A disk is rotating about an axle through its center. A line is marked on the disk from the axle to the edge of the disk to follow the rotation. When the disk rotates, the line rotates with it.
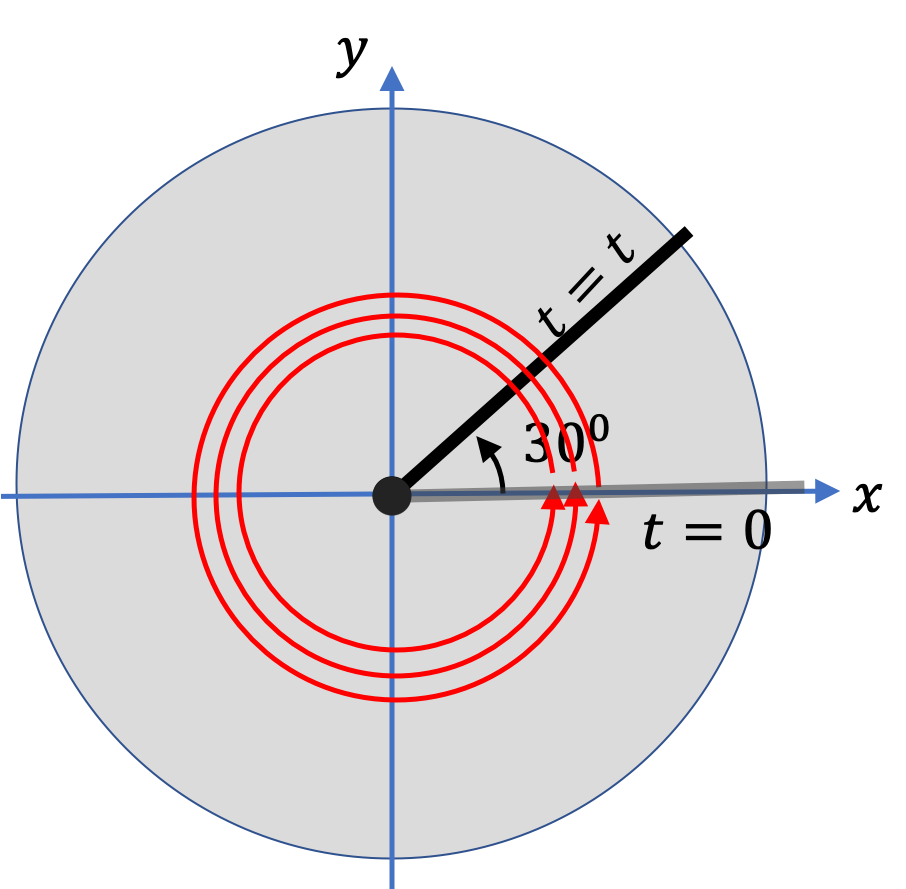
Choose a Cartesian coordinate system so that, at \(t=0\text{,}\) the line on the disk is in the direction of the positive \(x \) axis.
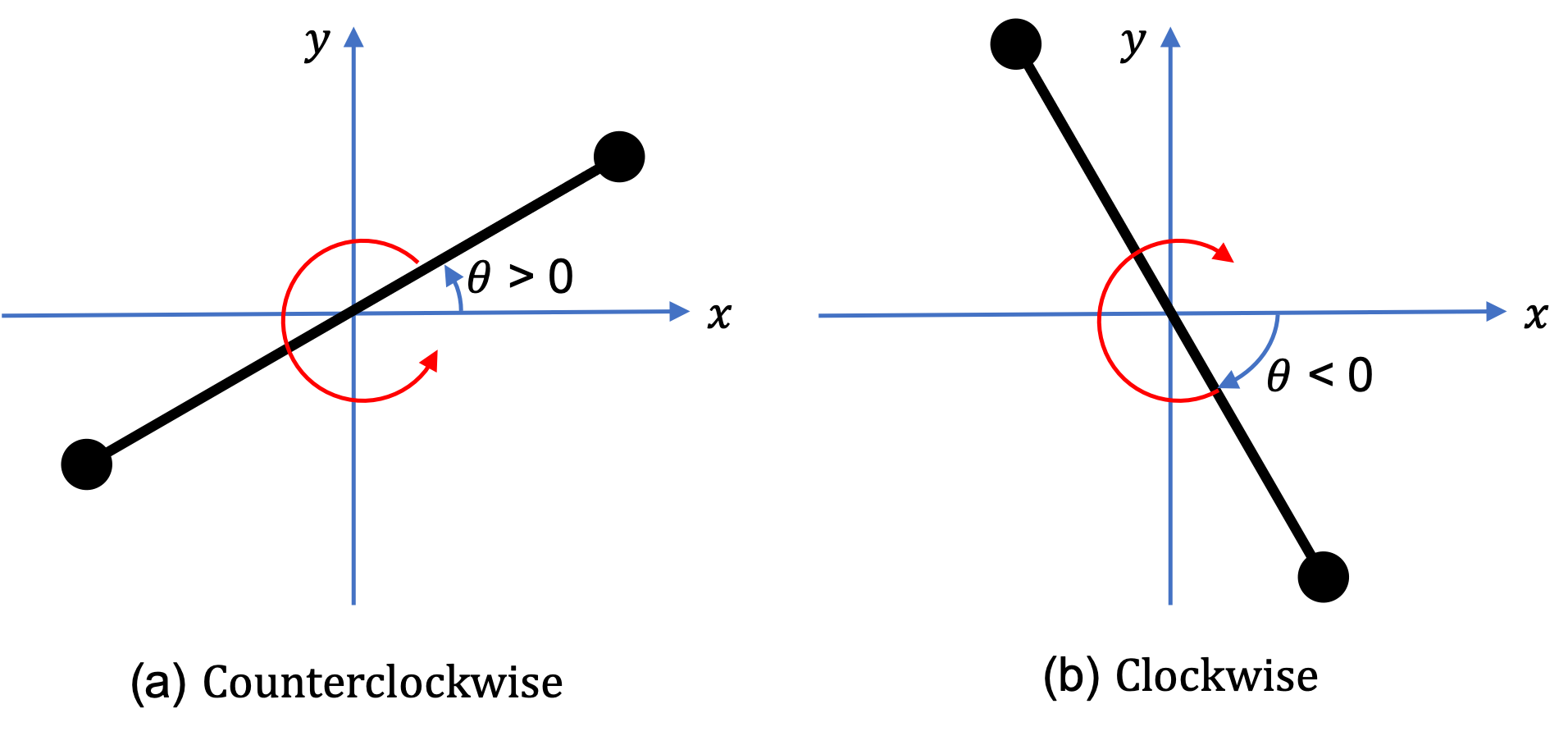
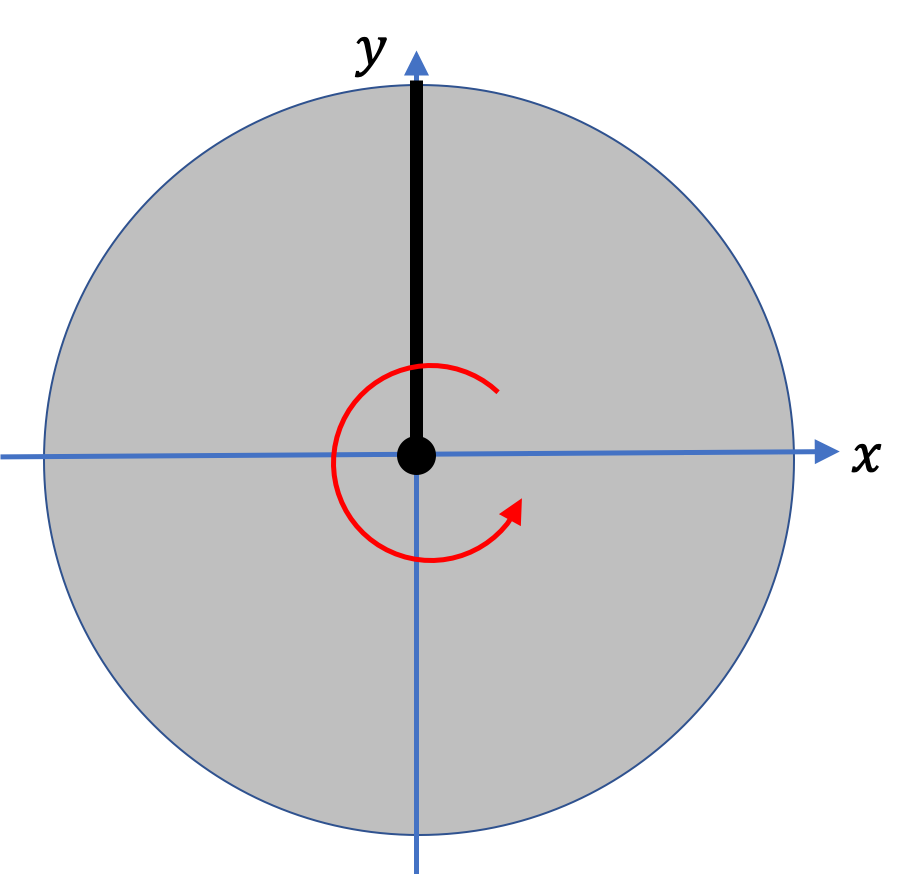
(a) When the disk is spinning counterclockwise, in \(10 \text{ sec} \) the line went around four times and ended up at \(90^{\circ}\) counterclockwise from the positive \(x \) axis. What is the total angle rotated in this time? Express your answer in (i) degrees, (ii) radians, and (iii) revolutions.
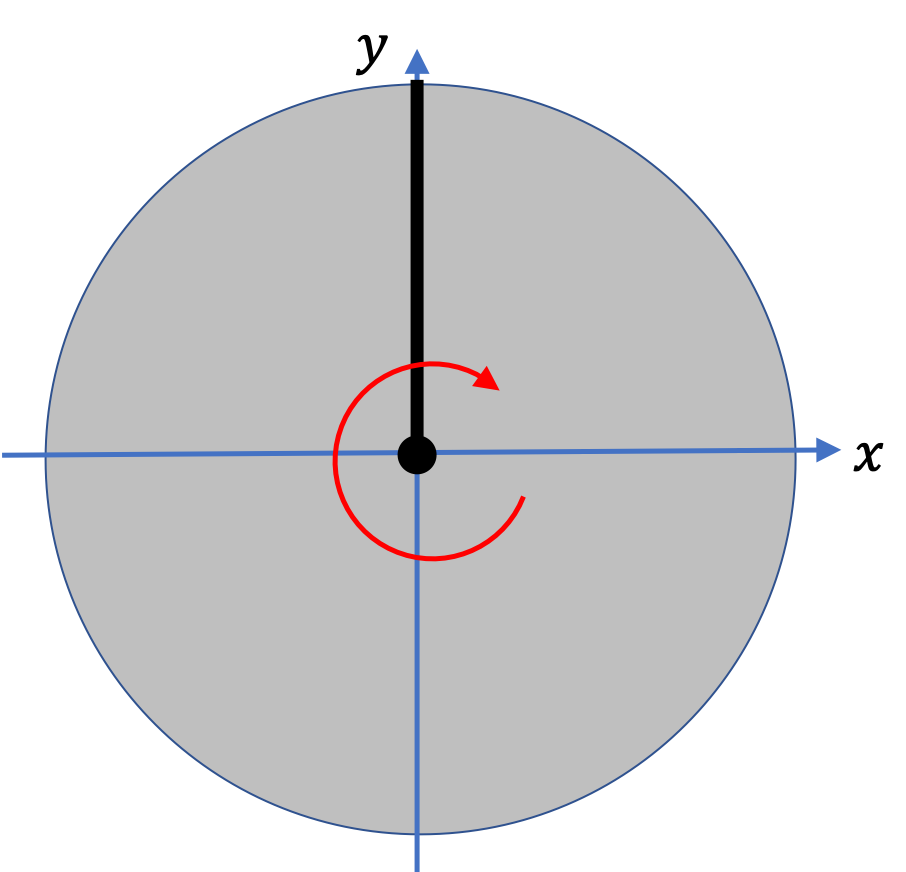
(b) When the disk is spinning clockwise, in \(10 \text{ sec} \) the line went around four times and ended up at \(90^{\circ}\) counterclockwise from the positive \(x \) axis. What is the total angle rotated in this time? Express your answer in (i) degrees, (ii) radians, and (iii) revolutions.
Hint.
(a) Add up all the angles. (b) Be careful here, while the disk is rotating clockwise, the final orientation is given in counterclockwise angle.
Answer.
(a) (i) \(1530^{\circ}\text{,}\) (ii) \(\dfrac{17}{2}\,\pi\text{ rad} \text{,}\) (iii) \(4.25\text{,}\) (b) (i) \(-1710^{\circ}\text{,}\) (ii) \(-\dfrac{19}{2}\,\pi\text{ rad} \text{,}\) (iii) \(-4.75\text{.}\)
Solution 1. a
(i) The angle of rotation is the cumulative angle. So, we have 4 full rotations and \(90^{\circ}\) more, all given in counterclockwise.
\begin{equation*}
\theta = 4\times 360^{\circ} + 90^{\circ} = 1530^{\circ}.
\end{equation*}
(ii) Since \(180^{\circ} = \pi\text{ rad}\text{,}\) this angle is same as
\begin{equation*}
\theta = 1530^{\circ} \times \dfrac{\pi\text{ rad}}{180^{\circ}} = \dfrac{17}{2}\,\pi\text{ rad}.
\end{equation*}
(iii) We can convert the angle in (i) to revolutions, by noting that one revolution has \(360^{\circ}\text{.}\)
\begin{equation*}
\theta = 1530^{\circ} \times \dfrac{ 1\text{ rev}}{360^{\circ}} =4.25\text{ revs.}
\end{equation*}
Solution 2. b
(i) The angle of rotation is the cumulative angle. so, we need all angles in the same sense. We have 4 counterclockwise full rotations and then some. That additional angle is given in clockwise, which we need to be counterclockwise, which will be obtained by subtracting \(360^{\circ}\) from the counterclockwise angle. counterclockwise.
\begin{equation*}
\theta = - 4\times 360^{\circ} + \left( 90^{\circ} - 360^{\circ} \right) = -1710^{\circ}.
\end{equation*}
(ii) Since \(180^{\circ} = \pi\text{ rad}\text{,}\) this angle is same as
\begin{equation*}
\theta = -1710^{\circ} \times \dfrac{\pi\text{ rad}}{180^{\circ}} = -\dfrac{19}{2}\,\pi\text{ rad}.
\end{equation*}
(iii) We can convert the angle in (i) to revolutions, by noting that one revolution has \(360^{\circ}\text{.}\)
\begin{equation*}
\theta = -1710^{\circ} \times \dfrac{ 1\text{ rev}}{360^{\circ}} = - 4.75\text{ revs.}
\end{equation*}