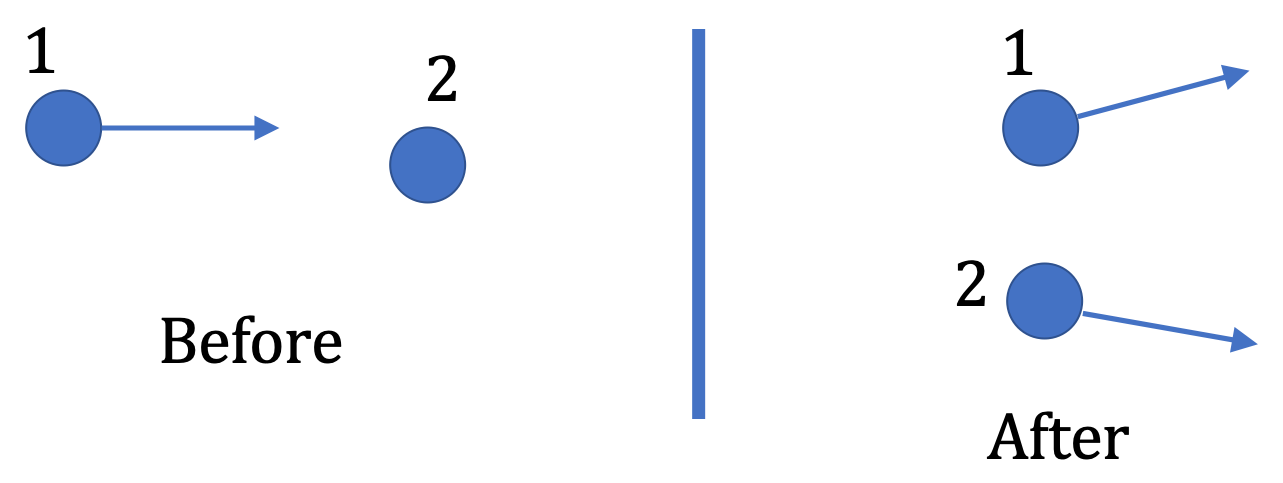Example 8.58. Head-On Elastic and Inelastic Collisions.
A ball of mass \(m \) moving at speed \(5\text{ m/s}\) hits another ball of mass \(2m\) initially at rest. The collision is head-on so that the motion after the collision is along the original line of motion.
(a) If the collision is elastic, what will be the velocities of the two balls after the collision?
(b) If the collision is not elastic, what will be the velocities of the two balls after the collision?
Answer.
(a) Ball 1 turns back with a new speed of \(\dfrac{5}{3}\text{ m/s}\) and ball 2 moves in the direction it was hit at speed \(\dfrac{10}{3}\text{ m/s}\text{.}\) (b) Many solutions. All solutions of \(v'_{1,x} + 2 v'_{2,x} = 5.\) where \(v'_{2,x} \ge 0\text{.}\)
Solution 1. a
Let us refer ball of mass \(m \) as ball 1 and the other ball as ball 2. Let us denote the velocities after the collision by placing a prime on the symbol, as is customary.
Momentum conservation
Momentum conservation is a vector equation, which we will handle component-wise. Let us use the line of motion to be the \(x \) axis with the positive \(x \) axis pointed in the same direction as the direction of motion of ball 1.
This gives us following velocity components of the two balls before and after the collision.
\begin{align*}
\amp \text{Before: } v_{1,x} = 5\text{ m/s},\ \ v_{2,x} =0, \\
\amp \text{After: } v'_{1,x} ,\ \ v'_{2,x}.
\end{align*}
The momentum conservation along \(x \) axis results in the following equation.
\begin{equation*}
m \times 5 + 2m \times 0 = m\times v'_{1,x} + 2 m \times v'_{2,x}.
\end{equation*}
Simplifying this equation, we get one equation in the two unknowns \(v'_{1,x} \) and \(v'_{2,x}\text{.}\)
\begin{equation}
v'_{1,x} + 2 v'_{2,x} = 5.\tag{8.48}
\end{equation}
Kinetic conservation since collision is elastic
Kinetic conservation gives us the following.
\begin{equation*}
\dfrac{1}{2}m\times 5^2 + 0 = \dfrac{1}{2}m\times {v^{\prime}_{1,x}}^2 + \dfrac{1}{2}\times 2m\times {v^{\prime}_{2,x}}^2 ,
\end{equation*}
which simplifies to the following equation in the two unknowns \(v^{\prime}_{1,x} \) and \(v^{\prime}_{2,x}\text{.}\)
\begin{equation}
{v^{\prime}_{1,x}}^2 + 2 {v^{\prime}_{2,x}}^2 = 25.\tag{8.49}
\end{equation}
Solving equations from conservation of momentum and conservation of kinetic energy:
We solve Eqs. (8.48) and (8.49) simultaneously to get the final velocities. One way to do that is to solve Eq. (8.48) for \(v^{\prime}_{1,x} \) and use that in Eq. (8.49) and solve the resulting equation for \(v^{\prime}_{2,x} \text{.}\) You can show that the resulting equation in \(v^{\prime}_{2,x} \) is
\begin{equation*}
3 \, {v^{\prime}_{2,x}}^2 - 10\, {v^{\prime}_{2,x}} = 0.
\end{equation*}
Therefore, we find two values for \(v^{\prime}_{2,x} \text{.}\)
\begin{equation*}
v^{\prime}_{2,x} = 0,\ \dfrac{10}{3}.
\end{equation*}
When \(v^{\prime}_{2,x} = 0\text{,}\) \(v^{\prime}_{1,x} = 5\text{,}\) and when \(v^{\prime}_{2,x} = 10/3\text{,}\) \(v^{\prime}_{1,x} = 5-20/3 =- 5/3\text{.}\)
Interpreting the result:
The final values for the two velocities have two possibilities (1) \((v^{\prime}_{1,x} = 5\text{ m/s}, v^{\prime}_{2,x} = 0)\text{,}\) or, (2) \((v^{\prime}_{1,x} = -5/3 \text{ m/s}, v^{\prime}_{2,x} = 10/3 \text{ m/s})\text{.}\)
Let’s look at each of these possibilities:
(1) \((v^{\prime}_{1,x} = 5\text{ m/s}, v^{\prime}_{2,x} = 0)\text{.}\) This says that the answer is as if no collision occured. This is just an artifact of this problem. We do not want this answer since we are concerned with the result of actual collision.
(1) \((v^{\prime}_{1,x} = -5/3 \text{ m/s}, v^{\prime}_{2,x} = 10/3 \text{ m/s})\text{.}\) The negative value of \(x \) component of the velocity of ball 1, says that the ball is moving towards the negative \(x \) axis. That means, after the elastic collision, both balls have precisely defined velocities, ball 1 turns back with a new speed of \(5/3\text{ m/s}\) and ball 2 moves in the direction it was hit at speed \(10/3\text{ m/s}\text{.}\)
Solution 2. b
When the collision is not elastic, we only have the conservation of momentum. We have already worked out the consequences of that in part (a) with the following relation between the final velocities given in (8.48).
\begin{equation*}
v'_{1,x} + 2 v'_{2,x} = 5.
\end{equation*}
This does not give a unique solution, but there are infinitely many possibilities as long as the values of \(v^{\prime}_{1,x} \) and \(v^{\prime}_{2,x} \) satisfy this equation and are physically resonable, which would demand that ball 2 should not have negative \(x \) component of the velocity since it was hit with a force directed towards the positive \(x \) axis.
Example anwers would be \((v^{\prime}_{1,x} ,\ v^{\prime}_{2,x} )\) \(= (0, 5/2), (1, 2), (-1, 3), \cdots \text{.}\) But, some mathematical answers of the above equation, such as \((7, -1)\) are not physically possible since force on ball 2 is in the direction of positive \(x \) axis can only cause acceleration towards the positive \(x \) axis.