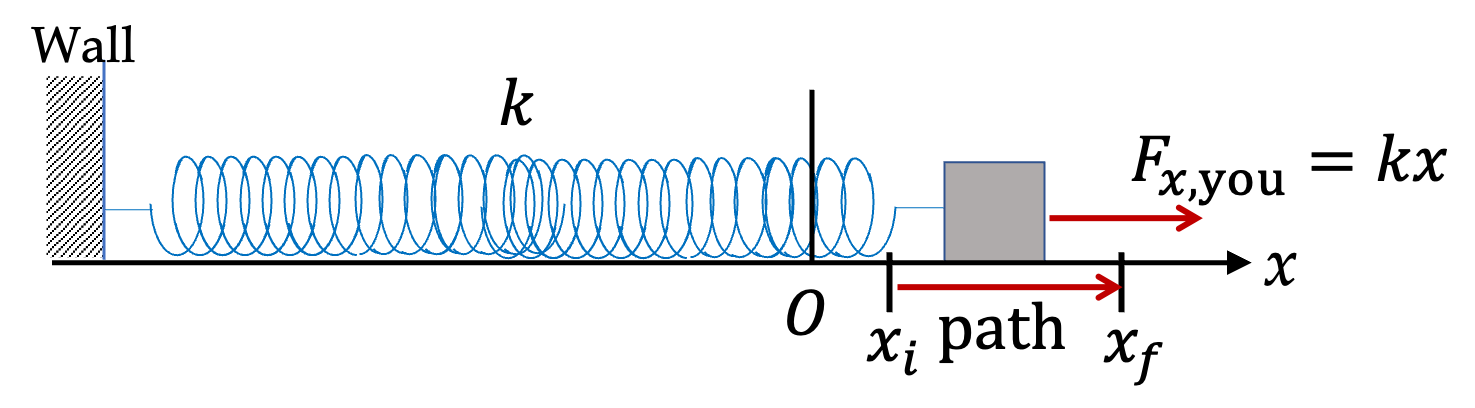
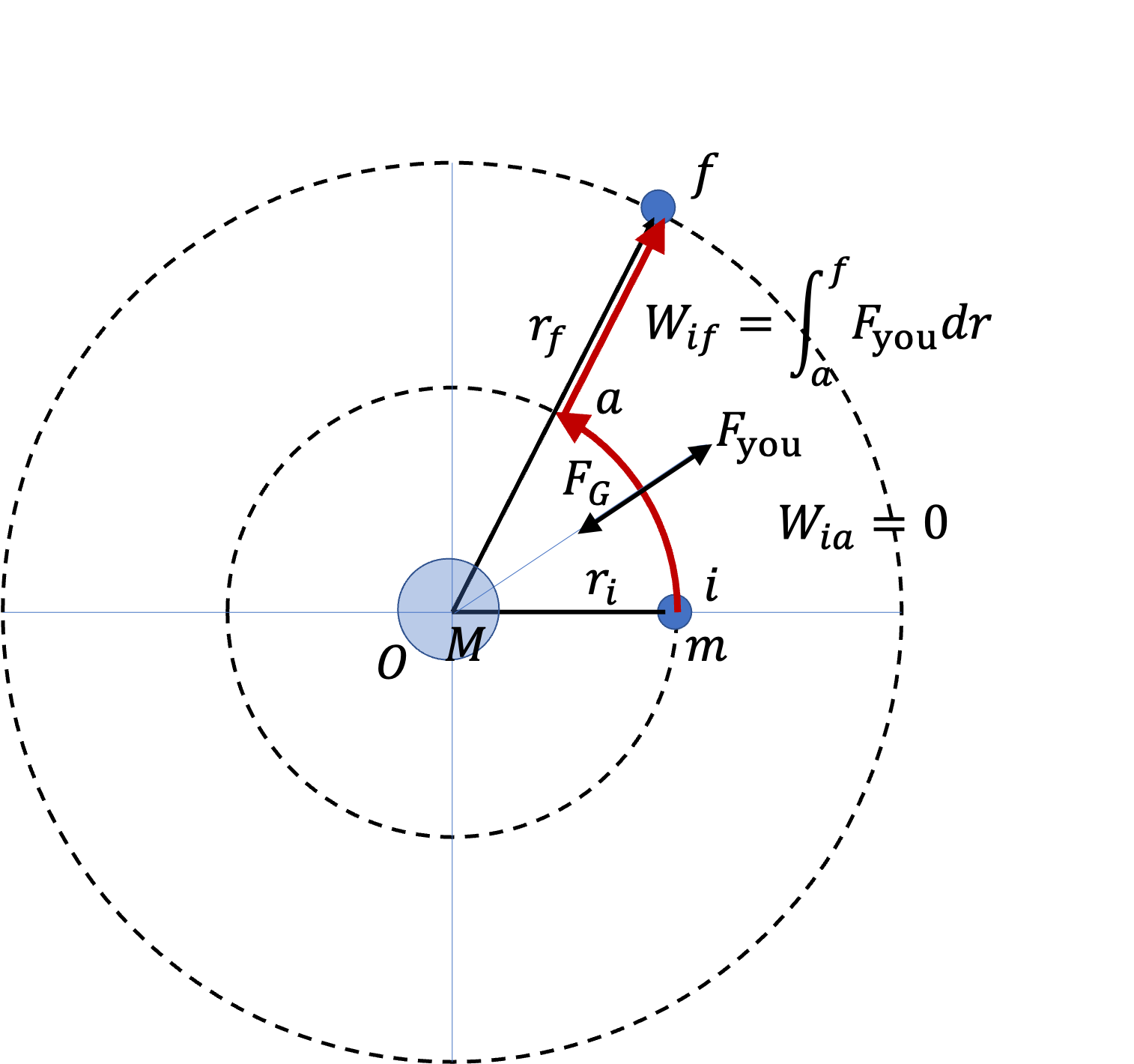
Previously we have studied energy due to motion, called kinetic energy. Now, we look at energy associated with position, which is called potential energy. It is based on the observation that work by a class of forces, which will be called conservative forces, do not depend on the path of motion but just the initial and final positions. Weight, spring force, Newton’s gravitational force, and Coulomb’s electric force are common examples of conservative forces.
We will denote potential energy by letter
\(U \) and sometimes by
\(\text{PE}\text{.}\) Experiment such as illustrated in
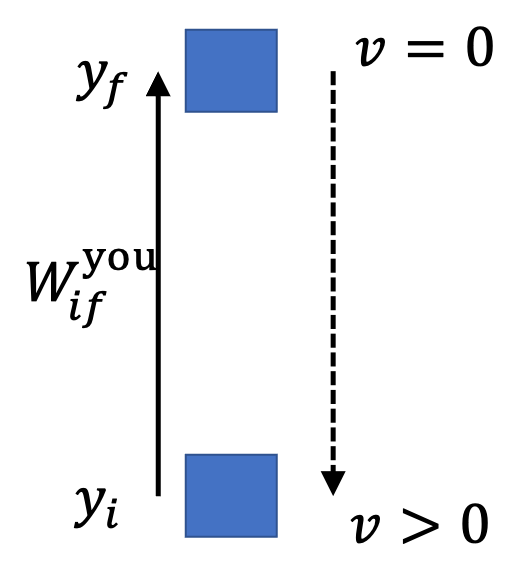
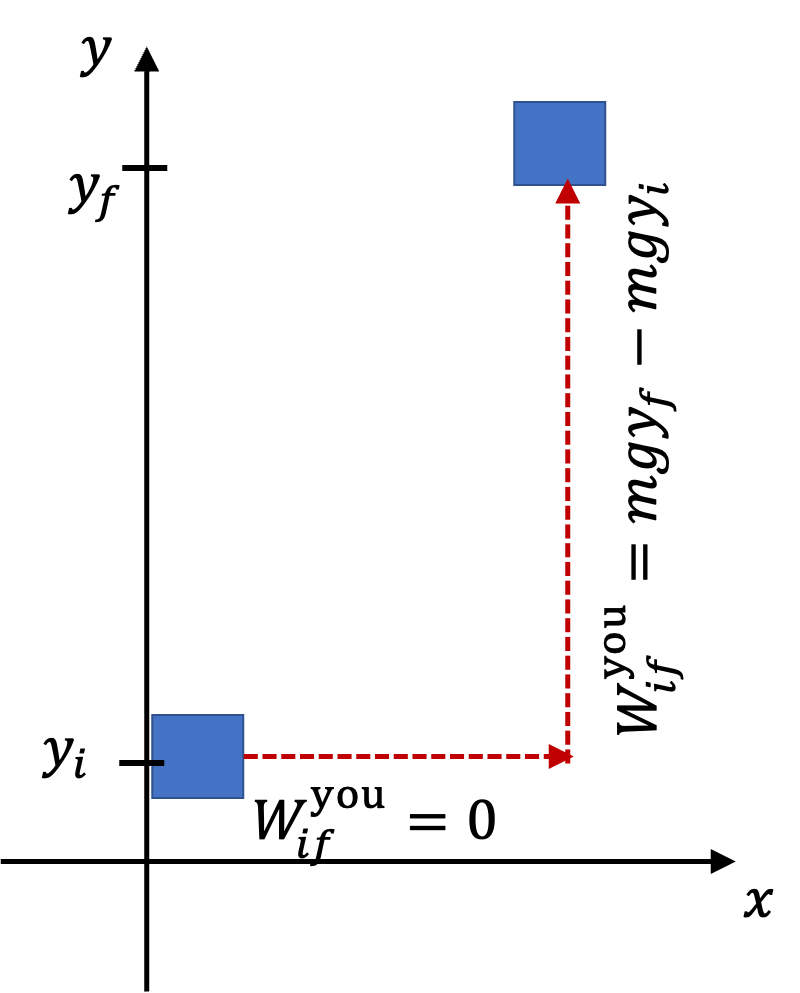
Figure 8.31 can be performed for every conservative force. In each case, the work you would do, while balancing the force, will end up being stored in the system as difference of potential energy of the system between initial and final positions. Let’s denote this difference by
\(\Delta U\text{.}\) Since your force is balancing the conservative force, the work done by the conservative force will be exactly opposite in sign. We can summarize these observations by the following.
\begin{equation}
W_{if}^\text{by you} = \Delta U = U_f - U_i = - W_{if}^\text{by conservative force}\tag{8.22}
\end{equation}
Taking initial point \(i\) to be a reference such that \(U_i=0\text{,}\) we can define potential energy of a particle at an arbitrary point in space, i.e., we get a otential energy function! Of course, reference will have to be chosen for various forces appropriately. For instance, for gravity, we choose initial point to any point whose \(y=0\text{,}\) i.e, any point in the horizontal \(xz\)-plane. Then, we get potential energy function \(U(x,y,z)\) f a praticle of mass \(m\) due to gravity at any point \((x,y,z)\) to be
\begin{equation*}
U_\text{weight}(x,y,z) = mgy.
\end{equation*}
For gravitational force, for \(U_i=GMm/r_i\) to be zero, the initial point has to be at a place where \(r_i = \infty\text{.}\) Then, the potential energy function of a particle of mass due to this force will be
\begin{equation*}
U_\text{gravitation}(r) = -\frac{GMm}{r},
\end{equation*}
where \(r = \sqrt{x^2+y^2+z^2}\) from the center of \(M\text{.}\) Let’s summarize these potential energy functions and their references for future use.
\begin{align}
\amp U_{\text{weight}} = mgy\quad \text{reference at } y=0.\tag{8.23}\\
\amp U_{\text{spring}} =\dfrac{1}{2}kx^2 \quad \text{reference at } x=0.\tag{8.24}\\
\amp U_{\text{gravitation}} = -\dfrac{Gm_1m_2}{r}\quad \text{reference at } r=\infty. \tag{8.25}\\
\amp U_{\text{coulomb}} = \dfrac{1}{4\pi\epsilon_0}\dfrac{q_1q_2}{r} \quad \text{reference at } r=\infty. \tag{8.26}
\end{align}
Often, we will write potential energy due to spring force in terms of change in length \(\Delta l\) of the spring rather than the coordinate of the block.
\begin{equation}
U_{\text{spring}} =\dfrac{1}{2}k(\Delta l)^2.\tag{8.27}
\end{equation}
Potential energy due to weight is also called gravitational potential energy, and is often written as \(m g h\) where \(h\) is height above some reference zero.
\begin{equation}
U_\text{weight} = m\,g\,h.\tag{8.28}
\end{equation}
Since points below a reference zero will have \(y\) coordinate negative, their heights will be negative also. Therefore, when you use \(mgh\text{,}\) make sure the sign is negative for points below the reference zero and positive for points above.