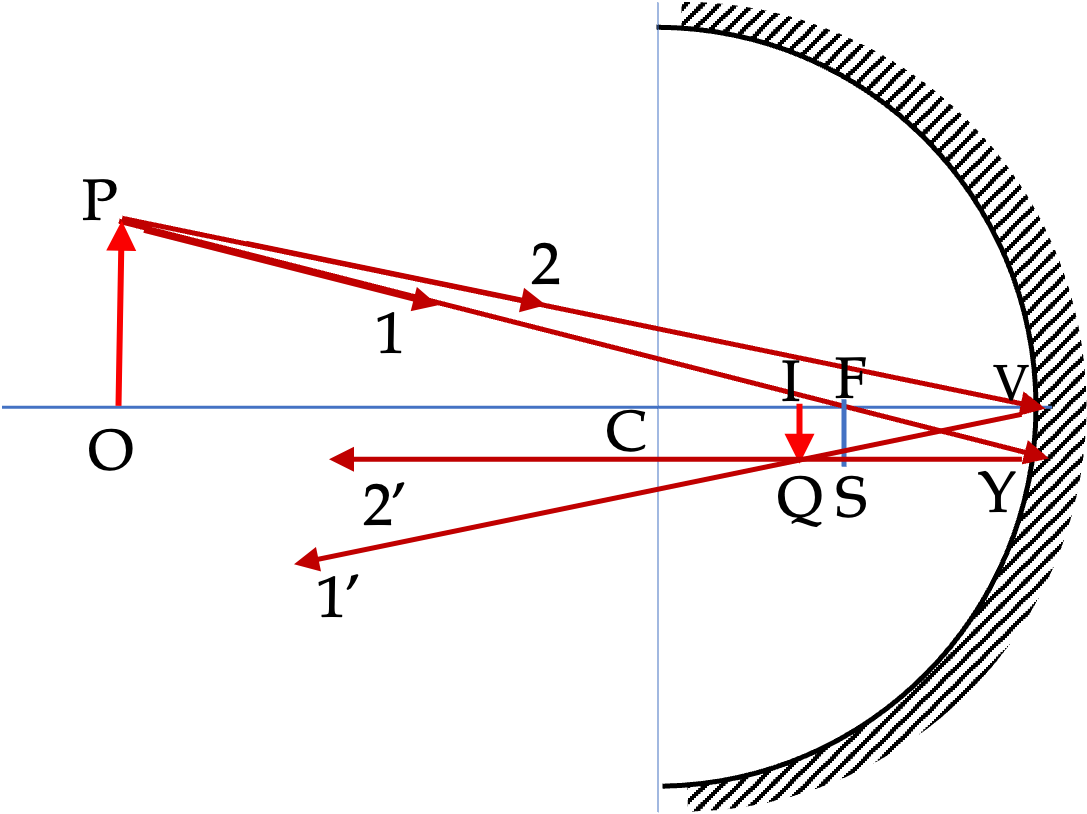
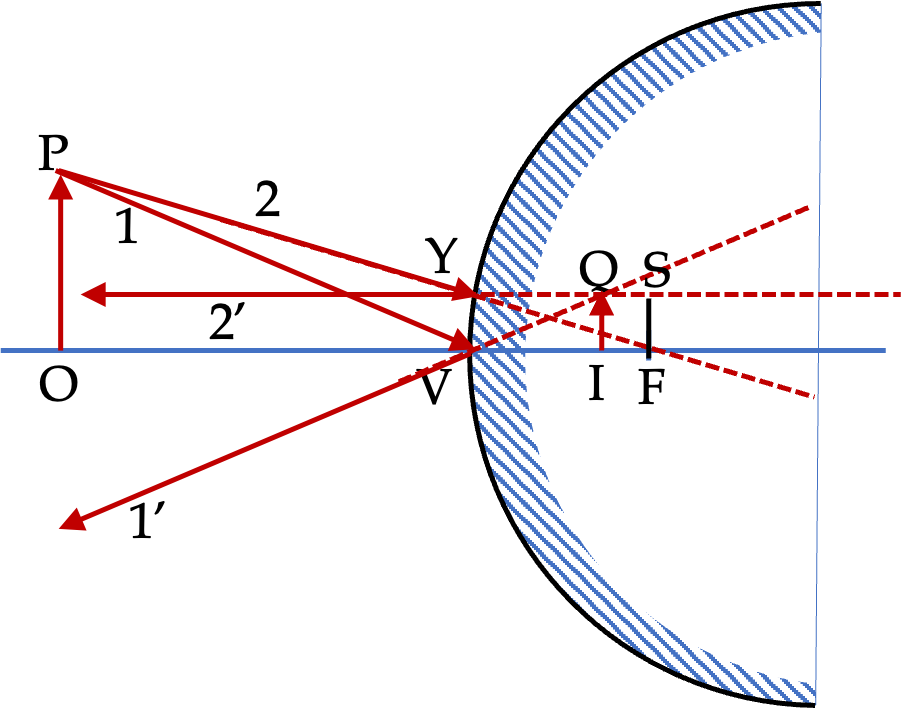
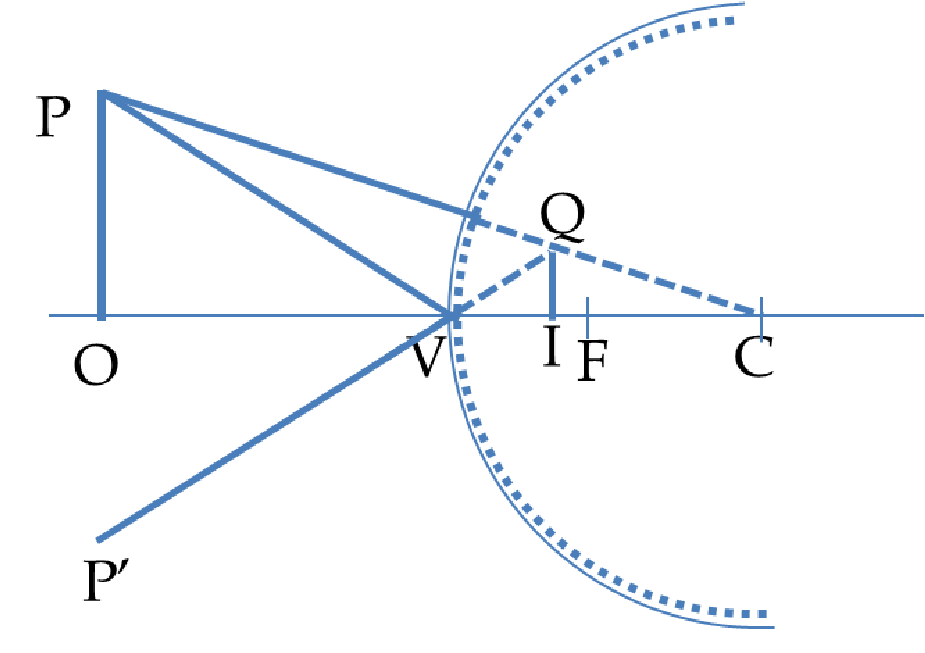
We will refer all horizontal distances from vertex V and all vertical distance from the optical axis OIV. Let \(R\) be the radius of the mirror. First notice that upon comparing the angles in triangles \(\triangle\text{OPV}\) and \(\triangle\text{IQV}\text{,}\) we find that these trinagles form a pair of similar triangles. Therefore, from plane geometry we can state that their corresponding sides must be proportional.
\begin{equation}
\frac{\text{VO}}{ \text{VI} } = \frac{ \text{OP} }{ \text{IQ} }.\tag{44.1}
\end{equation}
Similarly, try to establish that triangles \(\triangle\text{OPF}\) and \(\triangle\text{SFY}\) are similar. That will give us the following relation.
\begin{equation}
\frac{\text{FO}}{ \text{SY} } = \frac{ \text{OP} }{ \text{FS} }.\tag{44.2}
\end{equation}
By construction, we also have
\begin{equation}
\text{IQ} = \text{FS}. \tag{44.3}
\end{equation}
In our calculations, we will assume that the rays make small angle with the optical axis. This is called paraxial approximation. Paraxial rays make small angle, e.g., \(\theta = \angle\text{PVQ}\) at the vertex, therefore we can make the follpwing approximations
\begin{align*}
\amp \sin\theta \approx \tan\theta \approx \theta.\\
\amp \cos\theta \approx 1.
\end{align*}
Using these approximations we will also have the following important relation.
\begin{equation}
\text{SY} \approx \text{VF}. \tag{44.4}
\end{equation}
\begin{equation}
\frac{\text{VO} }{ \text{VI} } = \frac{ \text{FO} }{ \text{VF} }. \tag{44.5}
\end{equation}
Since \(\text{FO} = \text{VO} - \text{VF}\text{,}\) we get the following after using this and then dividing both sides by \(\text{VO} \text{,}\) and then rearranging terms.
\begin{equation}
\frac{ 1 }{ \text{VO} } + \frac{ 1 }{ \text{VI} } = \frac{ 1 }{ \text{VF} }. \tag{44.6}
\end{equation}
We now define symbols \(p\text{,}\) \(q\text{,}\) and \(f\) to represent the geometric distances as follows.
\begin{align*}
\amp p = \text{VO} = \text{object distance}, \\
\amp q = \text{VI} = \text{image distance}, \\
\amp f = \text{VF} = \text{focal length} = \frac{R}{2}.
\end{align*}
Note that the distance \(\text{VF}\) is equal to half the radius of the curvature of the mirror. That is, focal length of a concave mirror is
\begin{equation}
f = \frac{R}{2}. \tag{44.7}
\end{equation}
Using these symbols, Eq.
(44.6) takes the following familiar form, which we will refer to as
concave mirror equation.
\begin{equation}
\frac{1}{p} + \frac{1}{q} = \frac{1}{f}, \tag{44.8}
\end{equation}