Section 36.6 The Wheatstone Bridge
Perhaps the most famous bridge circuit is the Wheatstone bridge, which is used to measure resistances accurately.
The Wheatstone bridge circuit, shown in Figure 36.6.1, consists of four resistors connected to form a quadrilateral. One of the sides of the quadrilateral contains the unknown resistor \(R_{\times}\text{,}\) another contains a variable resistor \(R_V\) and the remaining two contain high precision resistors \(R_1\) and \(R_2\text{.}\) A voltage source V is connected to two opposite corners.
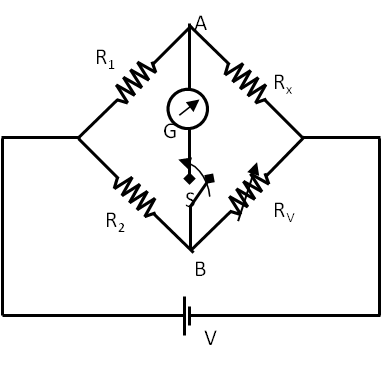
To detect the balance in the circuit, a sensitive detector of voltage difference, called a galvanometer G with a switch is connected between the other two corners of the bridge. A galvanometer is a device that detects current using the magnetic property of current which we will study in a later chapter. When the resistors are related in a particular way, there is no potential difference between the points marked A and B, and the galvanometer shows no deflection. This condition is called the null condition and the circuit is said to be balanced.
When there is no current in the AGB branch, then the circuit becomes simply a circuit of two resistances \(R_1+R_{\times}\) and \(R_2+R_V\) in parallel, and we can use the simple parallel circuits analysis to figure out the relation at the null condition.
At the null condition, let current \(I_1\) flow through the upper branch containing \(R_1\) and \(R_\times\text{,}\) and \(I_2\) flow through the lower branch containing \(R_2\) and \(R_V\text{.}\) At the null condition, the potential drop across \(R_1\) will equal the potential drop across \(R_1\text{.}\) Similarly, the potential drop across \(R_\times\) will equal the potential drop across \(R_V\text{.}\) Therefore, we will get
Eliminating currents from these equations by dividing each side gives the Wheatstone null equation, (36.6.1).