Section 2.1 Paper I
Problem 2.1.1. Q1. Static Equilibrium.
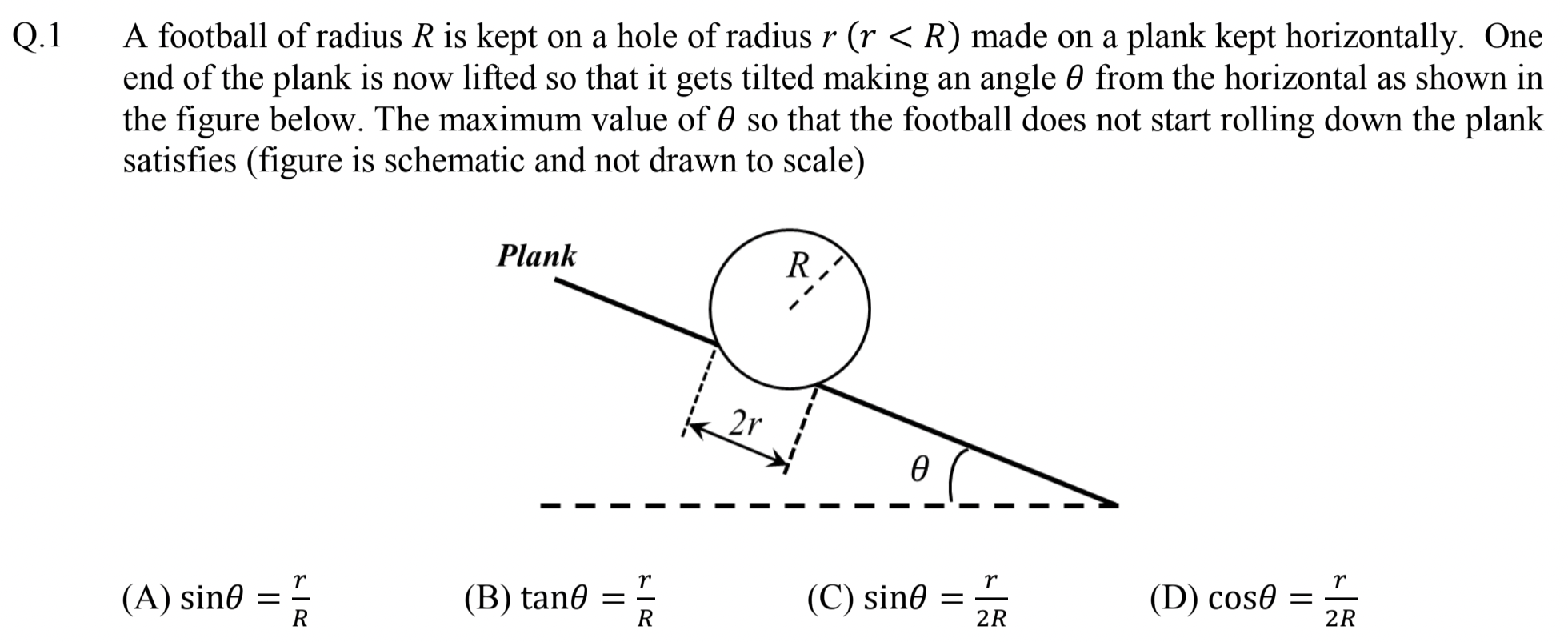
Static Equilibrium
(A).
Figure 2.1.2 shows the situation for incline at which \(N_2\) is vertical balancing \(mg\) and hence \(N_1\) must be zero. for larger angle, torque about suport for \(N_2\) will not be balanced. Hence, we need to figure out this angle.
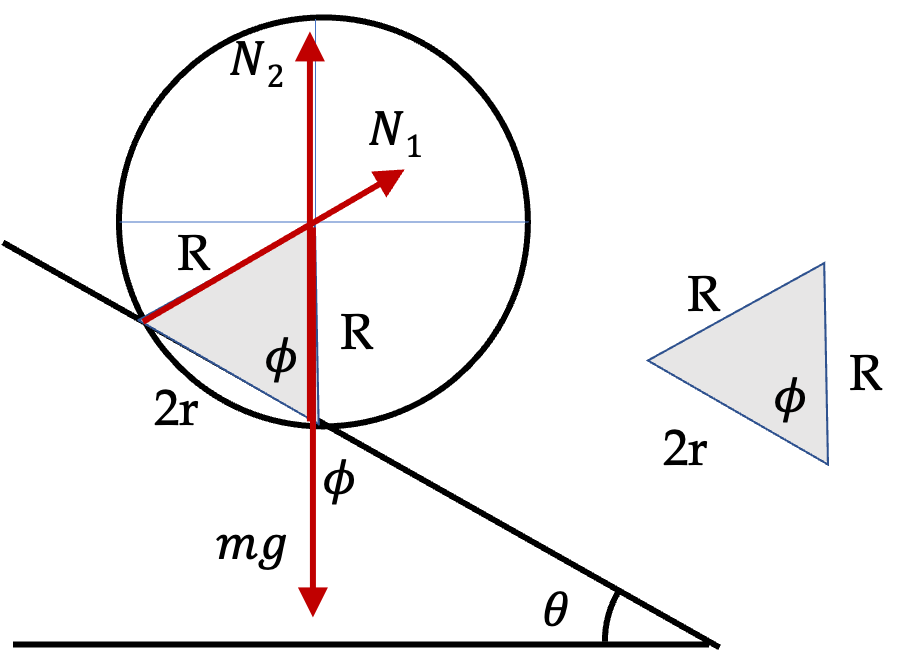
By drawing a vertical to the side \(2r\) in the triangle, we can immediately see that
Since \(\phi =90^\circ - \theta\text{,}\) \(\cos\phi = \sin\theta\text{.}\) Hence,
This is choice A.
Problem 2.1.3. Q2. Eddy Current.

Magnetic braking due to Eddy currents
(B).
Figure 2.1.4 shows view from above. When magnet is moving from one place to next, eddy currents are induced in loops in the front and behind the magnet.
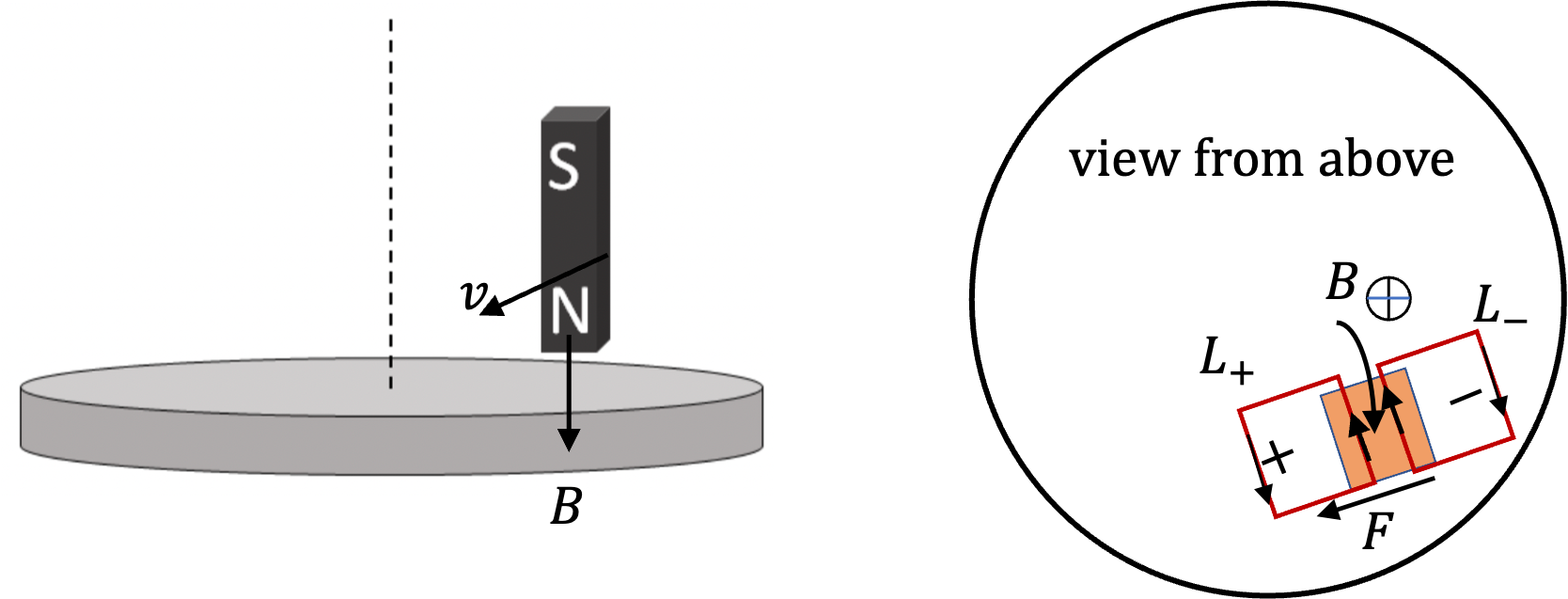
In the front of the magnet, say loop \(L_+\text{,}\) since magnetic field (down direction) lines will be increasing in eddy loop, the induced current will circulate in the counterclockwise sense. In the behind the magnet, say in loop \(L_-\text{,}\) current will circulate in the clockwise sense.
Current at the location of the magnet will be such that magnetic force on the induced current will be in the forward direction, i.e., in the same direction as the motion of the magnet. Therefore, answer will be: (B) rotate in the same direction as the direction of magnet’s motion.
Problem 2.1.5. Q3. Rolling Motion.



Rolling Motion
(B).
Ruler will move a distance that a point A on the axle will move due to ruler not slipping on the axle. Roller, on the other hand will move a distance that a point P on the edge of the roller will move.
Since Axle and roller will rotate same amount of angle, say \(\Delta \theta\text{.}\) The distance moved by A and P will be
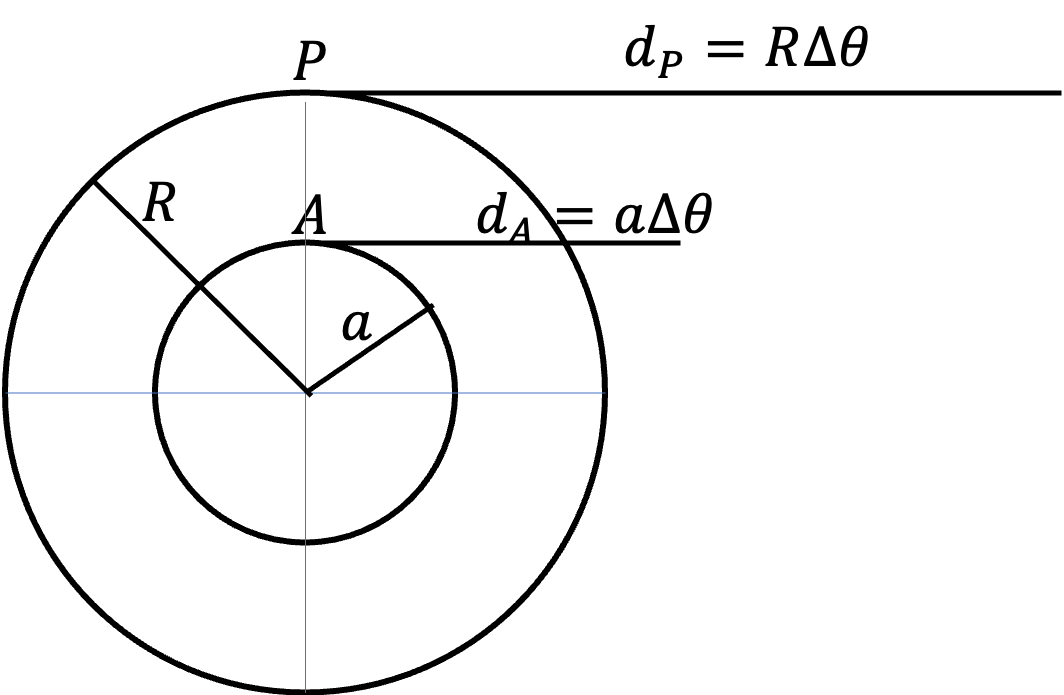
Therefore, by taking ratio we get
In the question, \(d_P=50\text{ cm}\text{,}\) and \(a/R = 1/2\text{.}\) Therefore,
Therefore, answer should be (B), where the ruler has its \(75\text{-cm}\) mark touching the axle.
Problem 2.1.7. Q4. Magnetic Torque.

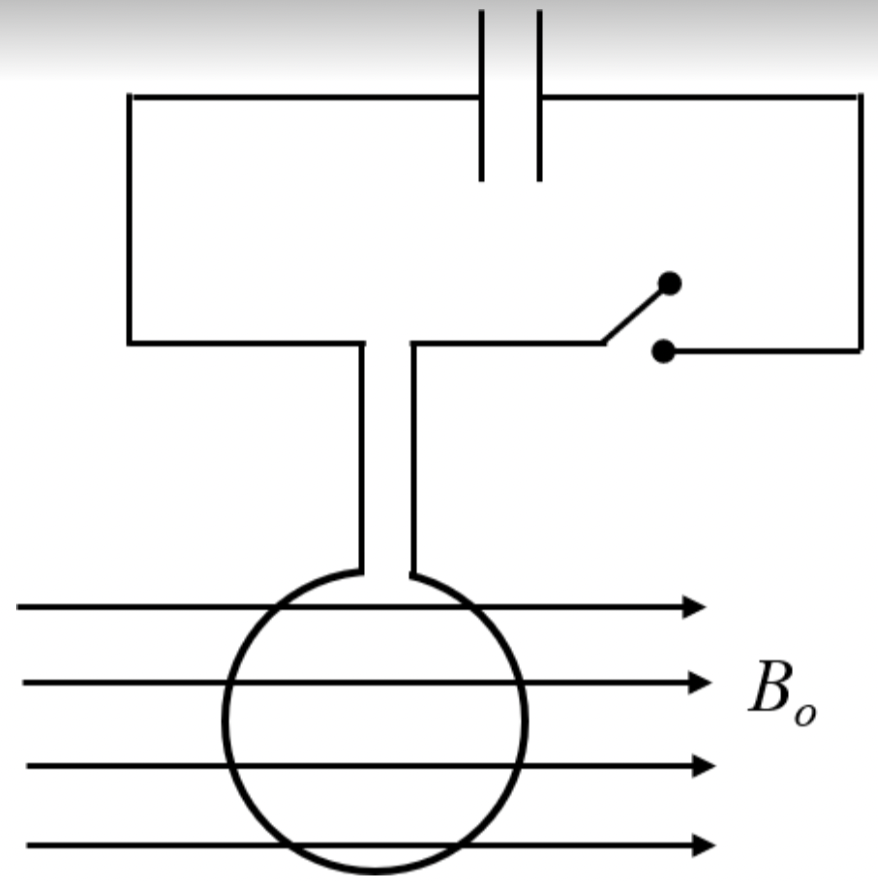
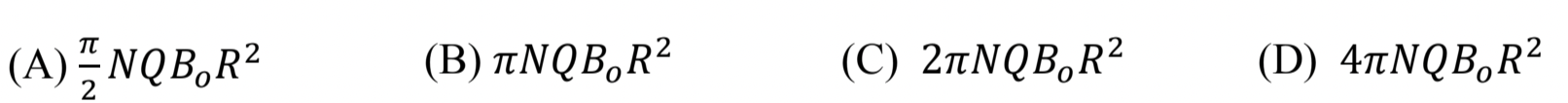
Think of Current Loop as a Magnetic Dipole.
(B).
Basic idea is to use Newton's law for rotation in the form
One way to find torque by magnetic force on a loop of current is to use equivalent magnetic dipole moment, \(\vec \mu\text{.}\) Then,
where
Let current in the loop be in counter-clockwise sense. Then, area vector \(d\vec A\) will be coming out of page. With \(N\) loops, the area will be \(N\) times as much. We get
with direction out-of-page. This will give torque
Here, only \(I\) is a function of time. Therefore, whe we integrate to get angular momentum, we will get
Since \(I=dq/dt\text{,}\) integrating \(I\) wil lgive us all the charge stored in the capacitor.
This is (B).
Problem 2.1.8. Q5. Wavefront.
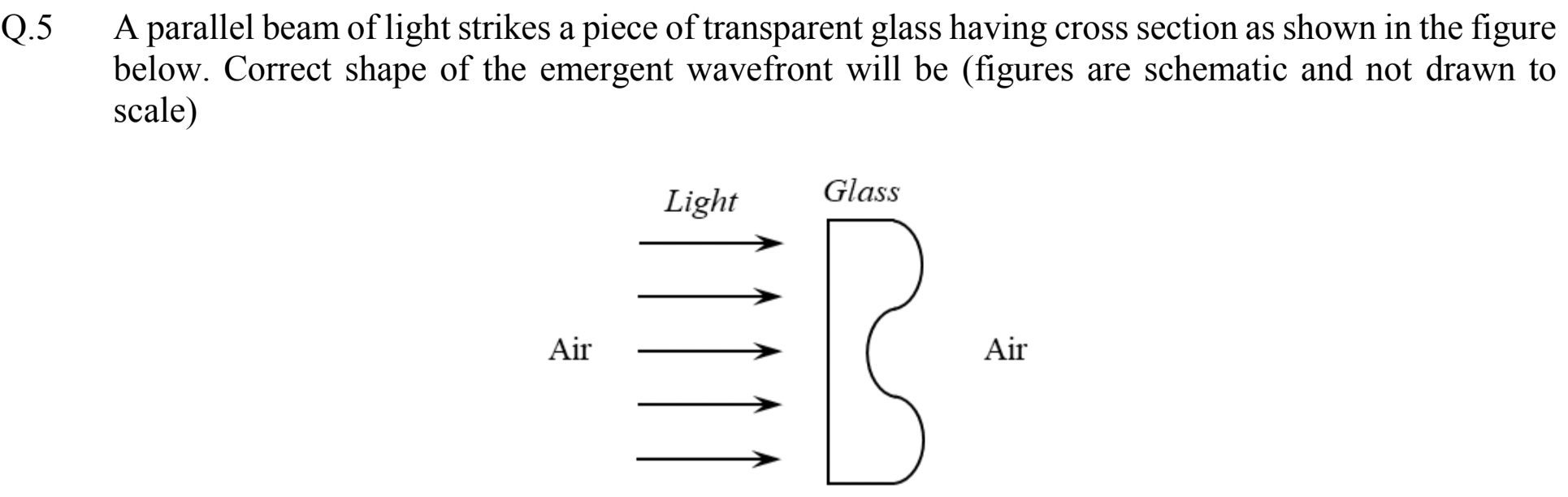
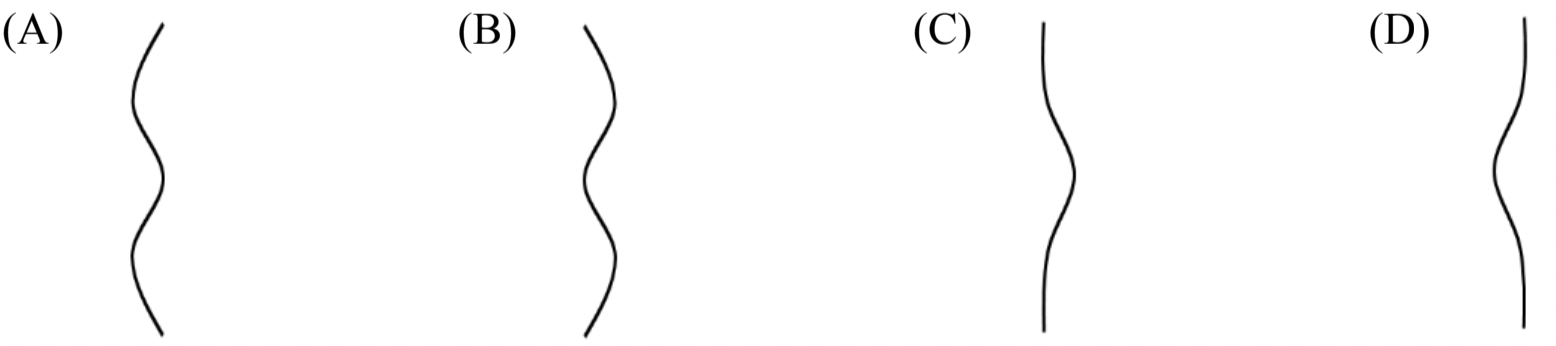
(1) Wavefront moves perpendicularly to the front with speed \(c/n\) in medium of refractive index \(n\text{.}\) (2) Original wavefront is planar.
(A).
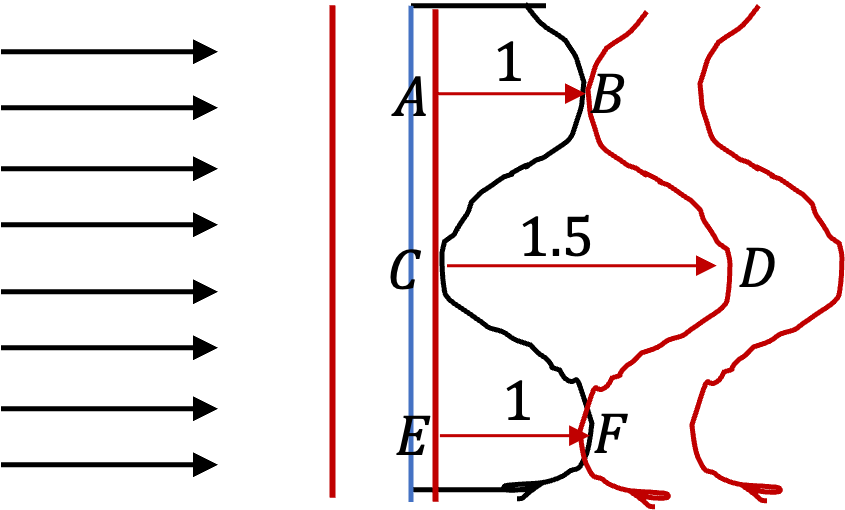
Figure 2.1.9 shows a plane wavefront entering glass where initiially it is a plane wavefront. The other end of the glass plate is curved. When exiting, it moves faster. In the time point A moves to point B, point C moves 1.5 times as far since for glass \(n=1.5\text{.}\) Similarly, point E moves to point F. The shape of the wavefront coming out wouold be as shown. This is choice A.
Problem 2.1.10. Q6. Static Pressure in Fluid.
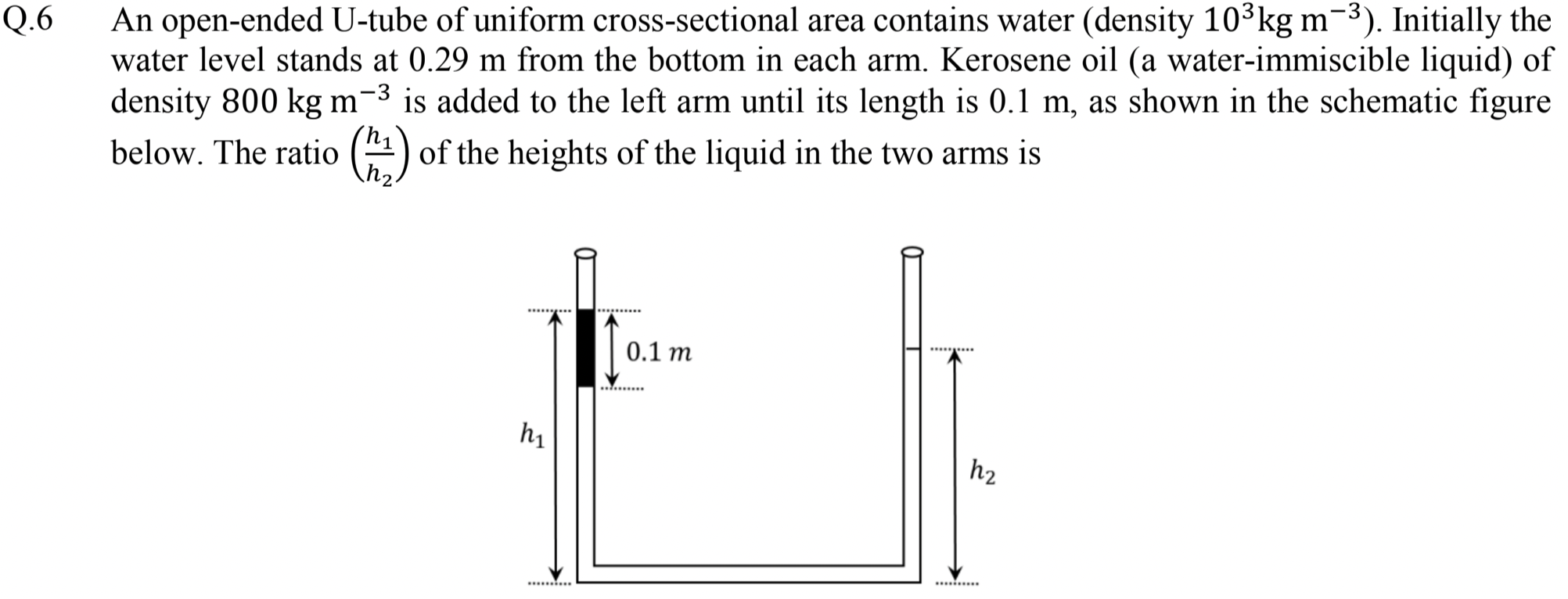

1. Equate pressure at same level in same fluid. 2. The denser fluid level on the two side goes down on one side by same height as it goies up on the other side.
B.
When we are in a single fluid, say within the water part, pressure at same horizontal level on the two sides will be same. That is, pressure in water at points A and B in Figure 2.1.11 will be same.
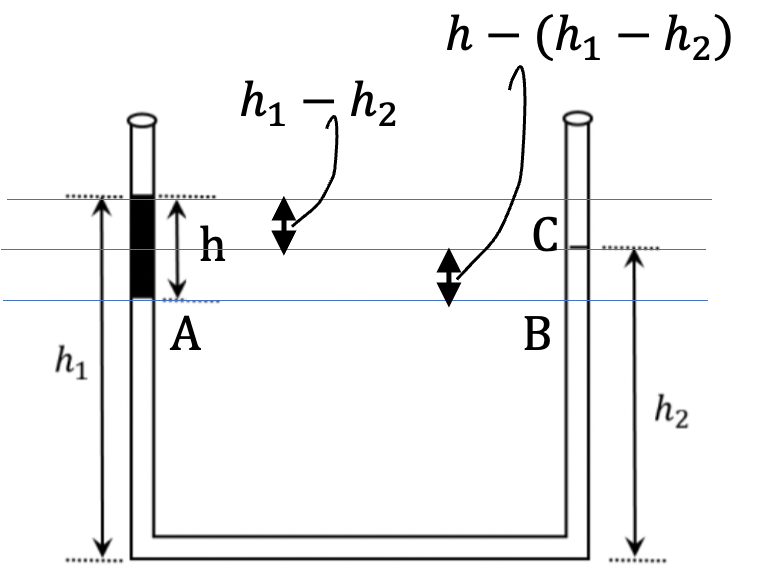
Thus, we will get the following equation.
Simplifying and then dividing both sides by \(\rho_1 h\) we get
From the original level of water (level D in Figure 2.1.12), we notice that point A would be as much below the original level D as point C will be above D since the two sides have the same area of cross-section.
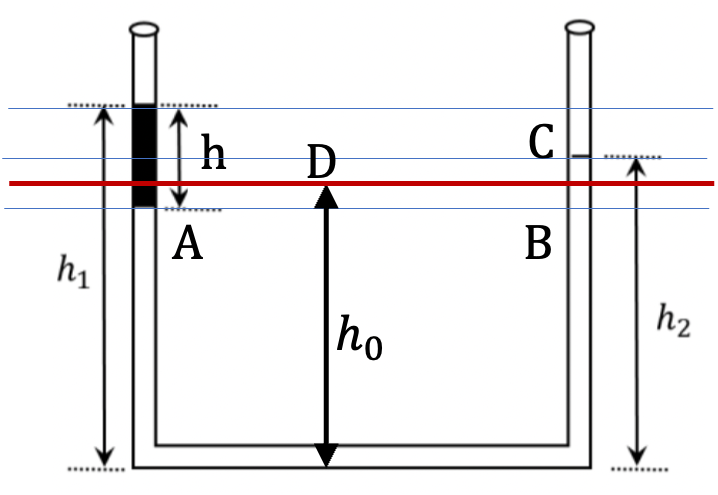
Using DC = BC/2 and BC from Figure 2.1.11 gives
Simplifying we have
From Eq. (2.1.1) and (2.1.2), we get
Therefore, the ratio is
Using the numerical values given,
This is choice B.
Problem 2.1.13. Q7. Bohr Model for Constant Force.

Use \(\vec F = \vec \nabla V\text{,}\) circular motion, energy conservation and Bohr quantization rule \(mvr = n\hbar\text{.}\)
(B) and (C).
Since any choice can be true or false, we need to test out each choice.
Bohr model is basically using a quantum rule for angular momentum \(mvr=n\hbar\) in classical equations.
From potential energy, we get radially inward force
Therefore, uniform circular motion will give
Energy conservation gives
Let's using the qunatum condition and attach subscript \(\text{}\) for the orbit identification. Transforming Eq. (2.1.4) as
and then using Eq. (2.1.3) we get
Using this in Eq. (2.1.3) gives
Thus (A) is incorrect and (B) is correct.
Using Eq. in Eq. we will get
Therefore, (C) is correct and (D) is incorrect.
Problem 2.1.14. Q8. Blackbody.

(A) and (B): Use Stephan-Boltzmann Law \(\Phi = P/A =\sigma T^4\text{.}\) (C) Use Wien's Displacement Law, \(\lambda_\text{peak} = b/T \text{.}\) (D) Energy in one photon is \(E=hc/\lambda\text{.}\)
(B), (C), (D).
We will need flux to solve for both A and B. Therefore, let us first calculate that.
To check (A), we multiply flux by the area \(A_e\) of the filament.
Therefore (A) is incorrect.
To check (B) we multiply flux by the area of the pupil.
Therefore (B) is correct.
To check (C) and (D), we use Wien's displacment law. It says
This is \(1160\text{ nm}\text{.}\) Therefore (C) is correct.
For (D), we use the fact that energy in one photon is
Now, we divide power in the eye by this number to get number of photons per second.
Therefore (D) is correct.
Problem 2.1.15. Q9. Dimensinal Analysis.

Check units on both sides match up.
(A) and (B).
For each choice we chech units on the left side to units on the right side. For instance, \(\alpha + p = 2\beta\) will mean somehow we have the following relation.
This must be a relation between quantities \([\text{position}]=[X^\alpha]\text{,}\) \([\text{acceleration}]=[X^p]\text{,}\) and \([\text{velocity}]=[X^\beta]\text{.}\) This relation will mean following units relation.
Let's check this using regular units.
Therefore, (A) is correct.
We check (B) similarly by starting with left side
Canceling common factors this simplifies to \(\text{m/s}\text{,}\) which is right side. Hence (B) is correct.
For (C) we get
which is not right side, which is \(\text{m}\text{.}\) Therefore (C) is incorrect.
For (D) we have for the left side
Clearly, this will not be \(\text{m/s}\text{,}\) the right side. Therefore, (D) is incorrect.
Problem 2.1.16. Q10. Projectile Motion.
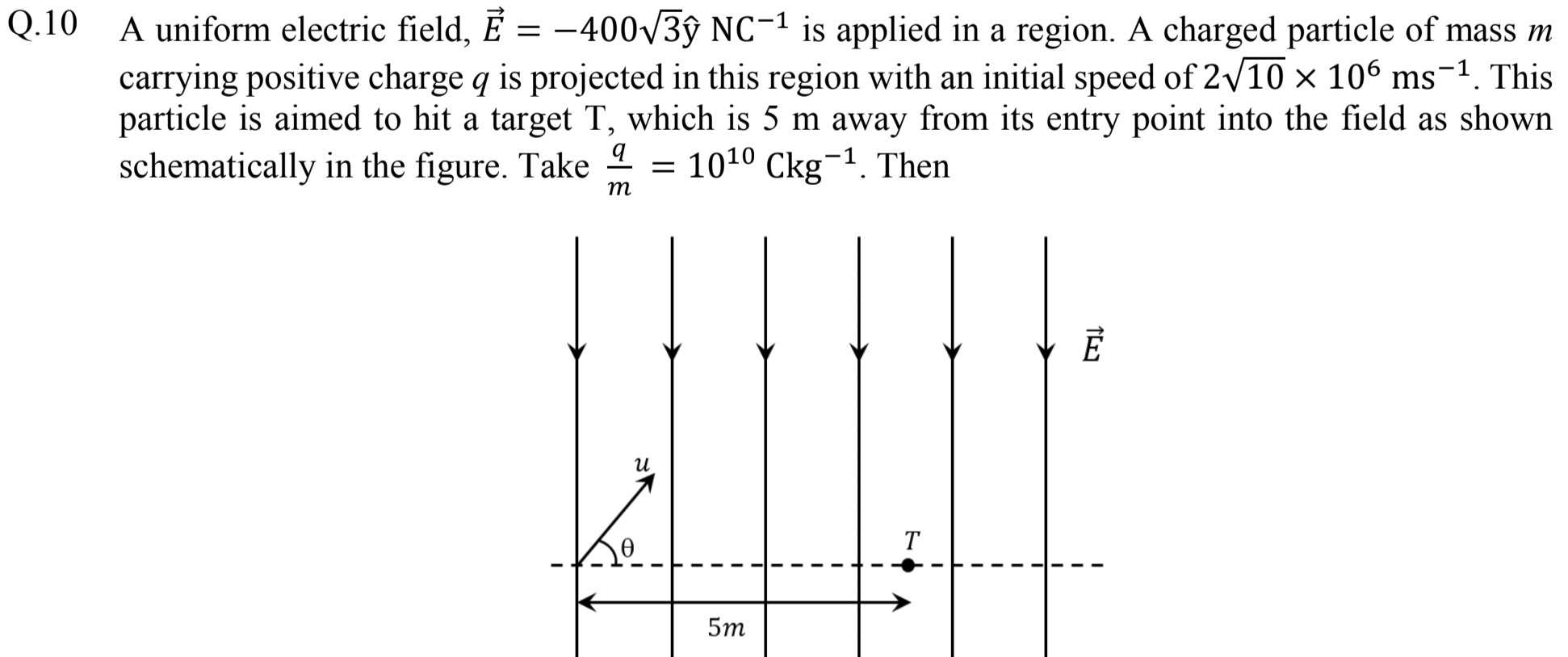

Standard projectile motion problem. Try not to start with numerical values.
(B), (C).
Figure 2.1.17 shows the projectile motion of the positively charged particle in an electric field. We will ignore gravity in this problem. Let \(u_x\) and \(u_y\) denote the Cartesian components of the intial velocity.
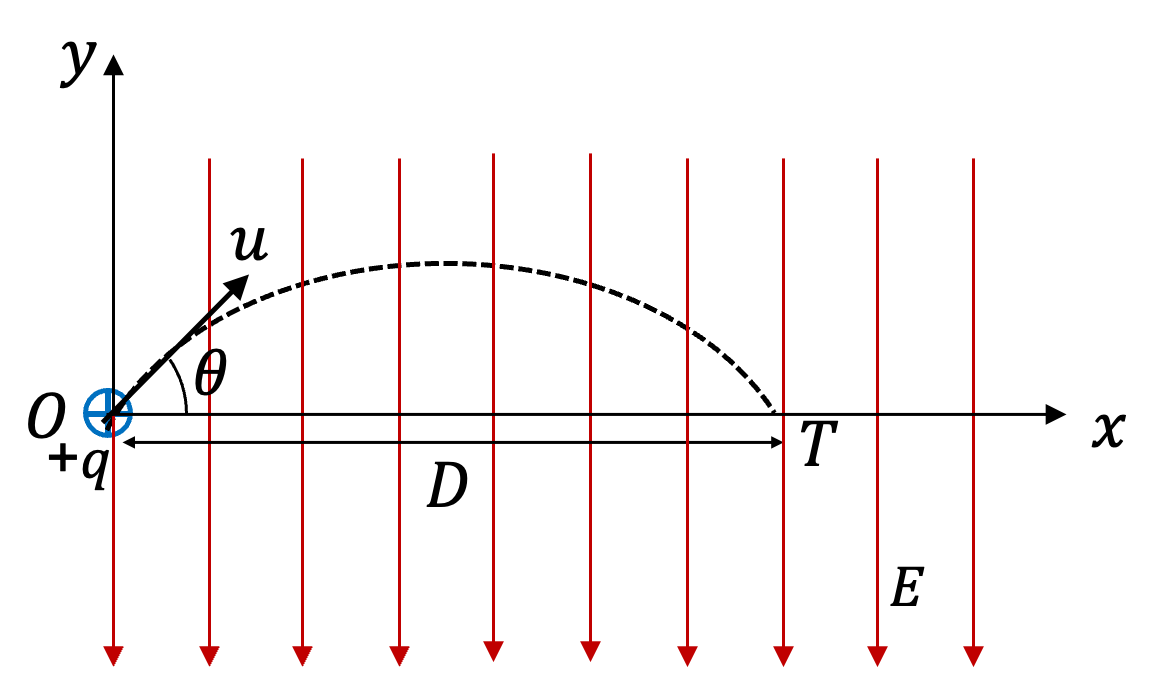
Acceleration has the following components.
Since \(E_y\) is negative and constant, constant acceleration is pointed down in the figure. From point \(O\) to \(P\text{,}\) the displacement has
Let \(t\) be the time from \(O\) to \(P\text{.}\) Now, we write relevaant equations of constant acceleration applied to this problem.
Therefore,
Now, using \(u_x=u\cos\theta\) and \(u_y=u\sin\theta\text{,}\) we get
Therefore,
Therefore, we have two chices for \(2\theta\) from which \(\theta\) will fall in the first quadrant.
Therefore \(\theta = 30^\circ,\, 60^\circ\text{.}\) Hence (A) is incorrect and (B) is correct.
We get \(t\) by
When \(\theta=30^\circ\text{,}\) we get \(t = \sqrt{5/2}\,\mu\text{s}\) and when \(\theta=60^\circ\text{,}\) we get \(t = \sqrt{5/6}\,\mu\text{s}\text{.}\) Therefore (C) is correct and (D) is incorrect.
Problem 2.1.18. Q11. Current in a Circular Conductor.

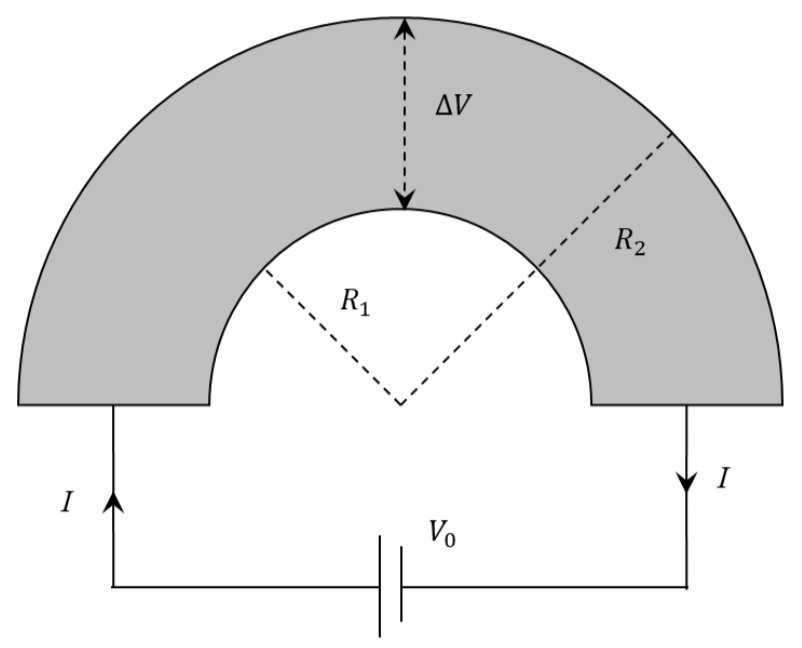
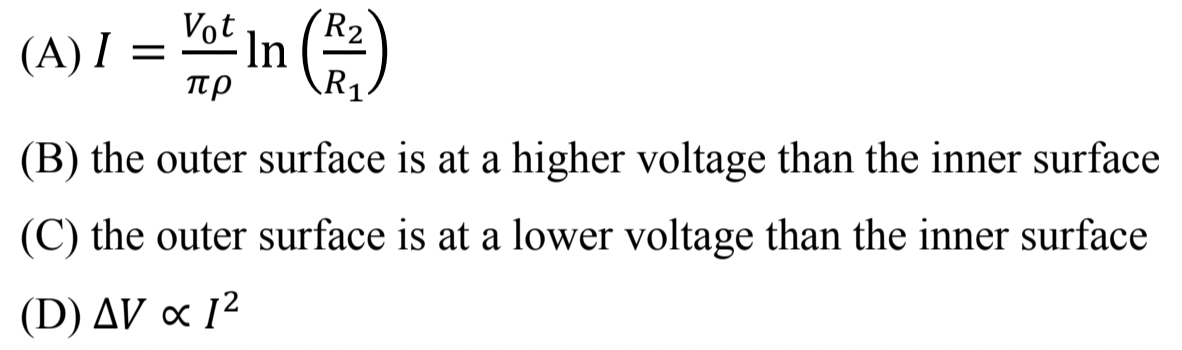
For (A), think parallel wires of infinitesimal widths. For (B) and (C) think of force on electrons. For (D), think circular motion and proportionality.
(A), (C), (D).
To check (A), we find resistance of the semicircular-shaped plate. We will think of this plate as parallel wires of thickness \(dr\) as shown in Figure 2.1.19. Since inverse of resistance, i.e., conductance, adds for parallel wires, we will work with conductance.
using \(R = \rho L/A\) formula, where \(\rho\) is resistivity.
Integrating, we get
Therefore, current will be
That is, (A) is correct.
To decide betwen (B) and (C), we just need to ask the sign of the charge on the current carrying particle. In metal the flowing particles are electrons. In a circular motion, the net force on the electron has to be towards the center. For force towards the centert, the inner surface as to be at higher voltage than the outer surface. Therefore (C) will be correct.
For (D), we look equations of motion of an electron at a radius \(r\text{,}\) e.g., one electron in the arc in Figure 2.1.19. This will be
In terms of current density, \(J=nev\text{,}\) where \(n\) is number density of conduction electrons, this becomes.
The left side when integrated from \(R_1\) to \(R_2\) will give \(\Delta V\) across the plate and the right side will be proportional to \(I^2\text{.}\) We are not asked for full expression, but just to test the proportionality. Hence,
Therefore, (D) is correct.
Problem 2.1.20. Q12. Ideal Gas.


Think of ideal gas law as \(p = n k_B T\text{.}\)
(A), (B), (C).
The ideal gas law in standard form \(pV=Nk_BT\) can also be written as
where \(n = N/V\text{,}\) number of molecules per unit volume, i.e., number density. Partial pressure in the two containers are
with difference in pressure \(\Delta p = p_1 - p_2\text{.}\)
For (A), we note that pressure from two sides on area of cross-section of tube will be
Therefore, (A) is correct.
For (B), we balance force on each molecule in the neck: force in part (A) due to partial pressure difference balanced by viscous force.
Canceling area \(S\) from both sides, we find (B) as correct.
For (C) we want \(n_1vS\text{.}\) From (B), we have
Therefore, (C) is correct.
In (C) \(\Delta n = n_1-n_2\) changes with time, hence, (D) is incorrect.
Problem 2.1.21. Q13. Static Equilibrium.

Assume max static friction and balance forces and torques.
\(25.6\text{ cm}\text{.}\)
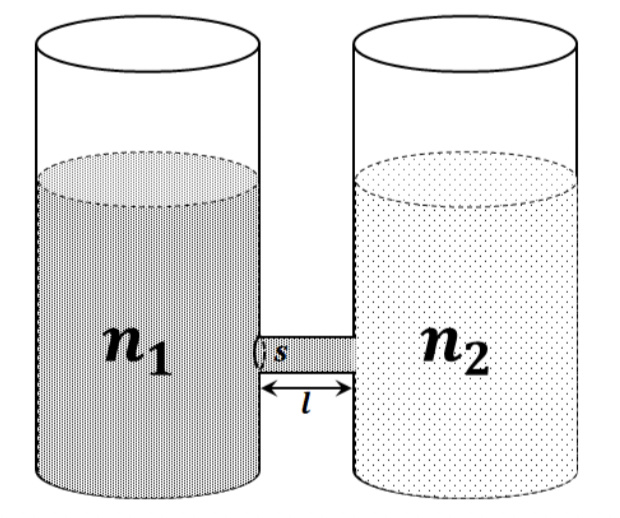
Figure 2.1.22 shows states of the ruler when the ruler starts to slide alongwith the forces on the ruler. I am assuming that static friction is maximum static friction, although that is not clear to me from the statement of the problem.
We wish to find \(x_R\text{.}\) I will leave distance in \(\text{cm}\text{.}\) We need only torque about center and horizontal force balance conditions. At the instant left finger starts to slip we will have
At the instant, the right finger starts to slip we will have
From these
Problem 2.1.23. Q14. Surface Tension.

Balance the force from surface tension acting at the rim by the outward force from varying pressure of the fluid through the bulging surface.
\(h=\sqrt{14}\text{ mm}=3.74\text{ mm}.\text{.}\)
From the discription of the problem, we interpret that by balancing forces on the extra water above the rim will give us the necessary condition for the stability of the bulging water. Let's think of bulging water in the shape of a cap and balance force on an element of bottom part of size \(R\Delta \phi\text{,}\) where \(R\) is radius of the rim and \(\Delta \phi\) is angle subtended at the center of the tube.
There are two forces on the element: (1) horizontal force due to surface tension and (2) horizontal component of the force by pressure in the fluid acting on semicircular shaped element of width \(R\Delta \phi\) and radius \(a=h/2\) as shown in Figure 2.1.24.
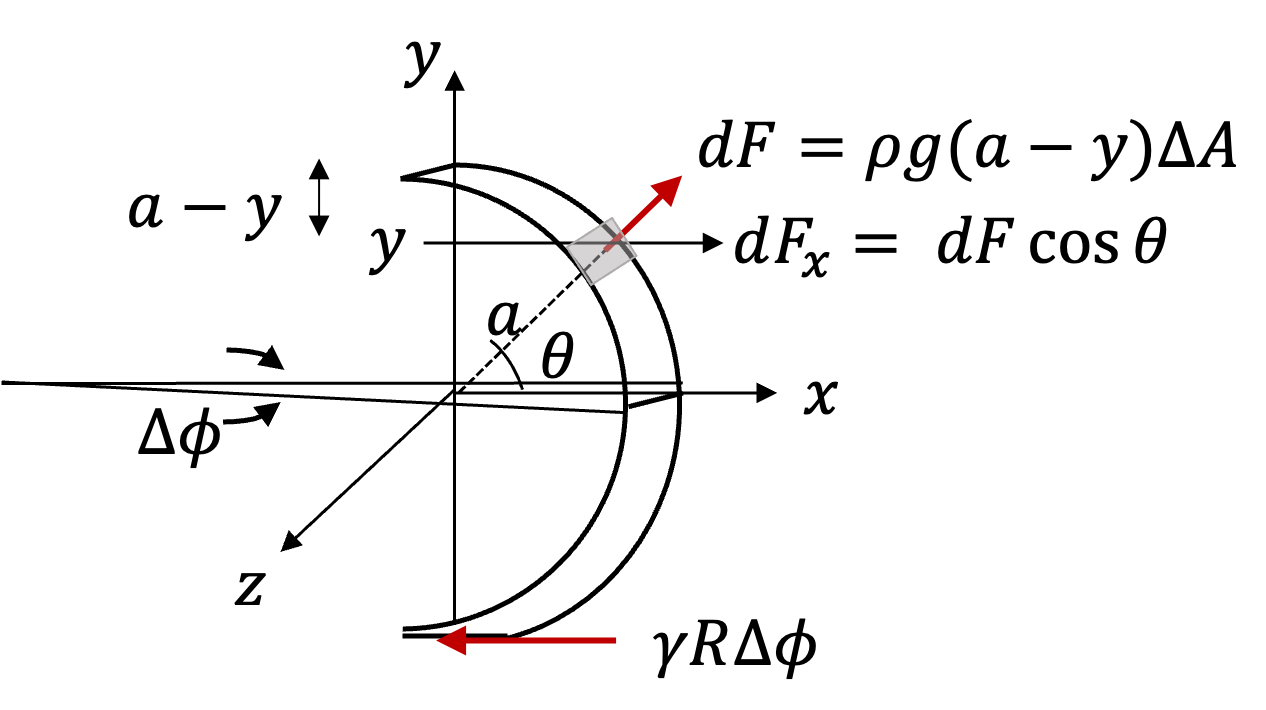
The force from surface tension will be horizontal at the rim, giving
The force due to fluid pressure on the strip shown in Figure 2.1.24 can be computed by adding contributions from elements of te strip. An area element of the strip will be
Then at coordinate \(y\) where height of fluid above is \(a-y\text{,}\) we get pressure \(\rho g (a-y)\text{.}\) Therefore, force has magnitude \(dF=\rho g (a-y)\Delta A\text{.}\) We want its horizzontal component to balance the horizontal force of tension. We have \(dF_x\) to be
Summing over all elements alog strip is done by going to the infinitesimal limit in \(\Delta \theta\) and integrating. Since \(y=a\sin\theta\text{,}\) we need to include it inside integration.
Balancing this with the force of tension yields
Simplifying this we get
Therefore,
Problem 2.1.25. Q15. Dipole Potential and Effective Spring Constant.

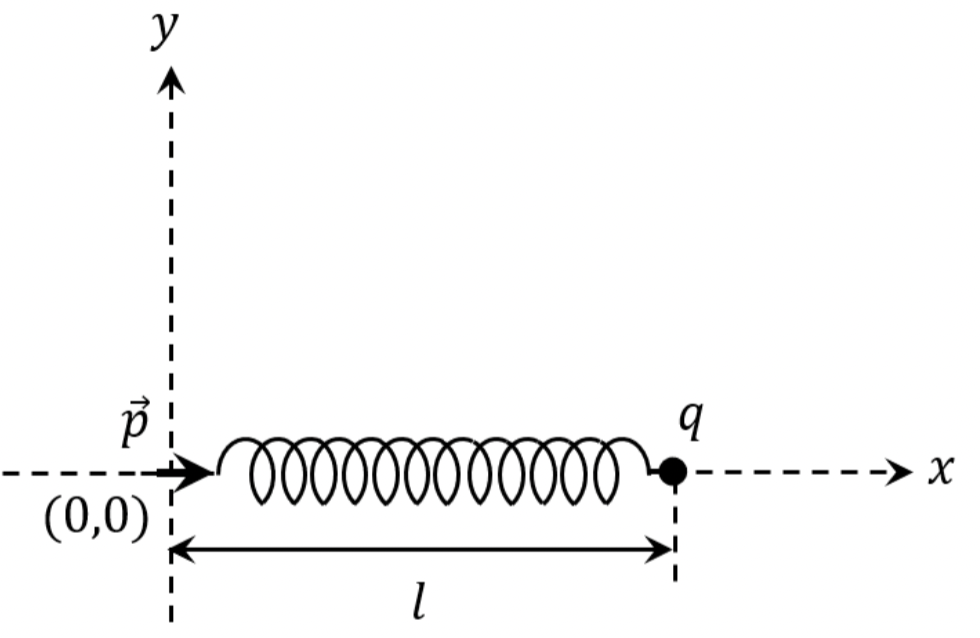
Find linear force at minimum of potential.
\(\delta = \pi = 3.14\text{.}\)
This question requires you to either figure out in the exam time or know from prior studies that electric potential of an electric dipole at point P is
where \(\vec r\) is displacement from dipole to point P and \(r\) is the distance. In the given diagram, we have
Therefore, we have
The total potential energy will come from this potential and the potential from spring. Let \(U(x)\) denote potential energy.
where I have multiplied \(V_\text{P}\) by \(q\) to get electric potential energy of \(q\) due to the dipole at origin. Now, we want the minimum of this potential energy and get effective spring constant by second derivative.
Therefore,
Now, we get effective spring constant from second derivative at the minimum.
From mass/spring oscillation we know that frequency will be
Therefore, \(\delta = \pi\text{.}\)
Problem 2.1.26. Q16. Isothermal and Adiabatic Expansions.

Use \(p=nRT/V\) for isothermal process and \(p = c/V^{\gamma}\) for adiabaitc process with \(c\) being a constant.
\(f = 16/9\text{.}\)
Ideal gas goes through the following state changes.
Each work is \(\int p dV\text{.}\) For isothermal step, we get
For adiabatic, we use \(pV^\gamma = p_2V_2^\gamma\text{,}\) constant.
But since \(p_1V_1=p_2V_2\) for isothermal step, this becomes
Hence, the ratio will be
Since \(He\) is a monatomic gas, \(\gamma = 5/3\text{.}\)
Therefore \(f = 16/9\text{.}\)
Problem 2.1.27. Q17. Doppler Effect.
Frequency will be higher when tuning fork is moving. Work with fundametal note only.
\(0.62\%\text{.}\)
The resonance occurs when length \(L\) of the tube is odd multiple of quarter of wavelength \(\lambda\text{.}\)
Here \(n=1\) is fundamental and others are overtones. Suppose we are working with fundamental resonance.
Using \(c\) for speed of sound, this condition in terms of frequency \(f\) of stationary tuning fork is
When tuning fork is movign with speed \(v\) towards the tube, the frequency to shift higher to \(f'\text{.}\)
New length \(L'\) required for resonance will have to be
The fractional change to get resonance in the moving tuning fork condition will be
Problem 2.1.28. Q18. Gauss's Law.

Use Gauss's law.
\(\frac{32}{5}\text{.}\)
According to Gauss's law flux through a closed surface is enclosed charge divided by \(\epsilon_0\text{.}\)
\(\phi_0\) is flus through the larger surface \(S_0\) and \(\phi\) is the flus through the smaller sphere. Therefore, we will have
For charges on a surface, we get charge enclosed by
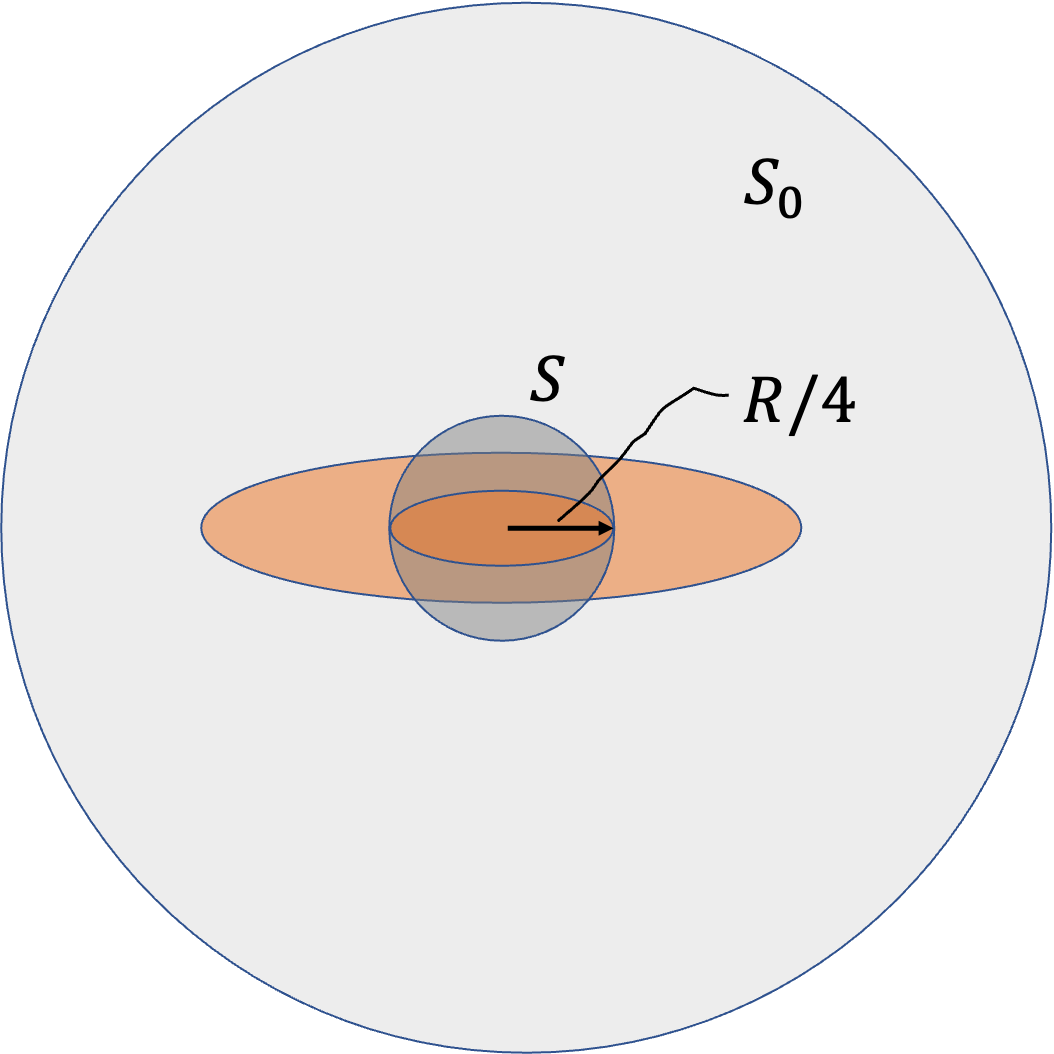
Since the area is a circular disk, its best to use polar coordinates.
Since integrand has only \(r\) dependence, integration over \(\theta\) gives just a factor of \(2\pi\text{.}\) Therefore, we need to do integration over \(r\) only. We will integrate to \(aR\) with \(a=1\) for full charge and \(a=1/4\) for up to \(R/4\text{.}\)
where \(b\) is just a common factor that will cancel out. Therefore,
Using these in the ratio of fluxes, we get
