Section 3.2 Paper II
Problem 3.2.1. Q1. Rotation of a Rod About its Edge.

CM moves in a circle.
(A), (C), (D).
We will use Figure 3.2.2 to do our calculations. The figure shows the three forces on the rotating rod. To get angular speed, we will use energy conservation. To get angular acceleration, we will use \(I\alpha = \tau\) for ration about O. To find \(F_N\text{,}\) we will set up \(F_y = m a_y\text{,}\) where \(a_y\) will be obtained from centripetal \((a_c)\) and tangental \((a_t)\) accelerations.
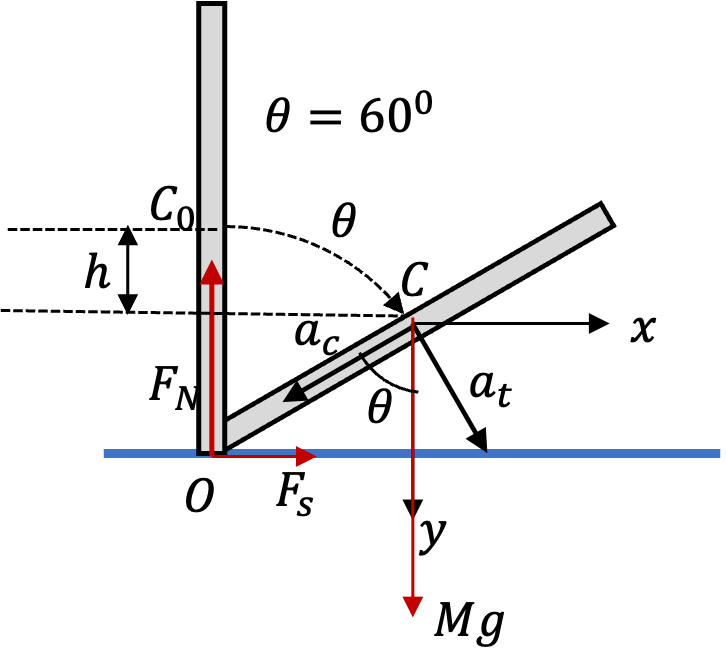
(A): Potential enegry drop is due to CM falling by height \(h\text{,}\) which will be
Kinetic energy will be rotational kinetic energy about \(O\text{.}\) Since that is the end of the rod, moment of inertia will be
Let \(\omega\) be angular velocity when at angle \(\theta\text{.}\) Energy conservation gives
Hence,
With \(\theta = 60^\circ\text{,}\) ie., \(\cos\theta = \frac{1}{2}\text{,}\) this gives
Hence choice (A) is correct
(B): To get angular acceleration, we apply \(I\alpha = \tau\) about O. The torque about O will be only from \(Mg\) at the CM with lever arm \(\frac{L}{2}\sin\theta\text{.}\) Therefore,
Hence, choice (B) is in correct.
(C): Since CM is moving in a circle of radius \(L/2\) with angular speed \(\omega\text{,}\) radial acceleration, i.e., centripetal acceleration, of CM will be
Hence, (C) is correct.
(D): To set up \(F_y = m a_y\text{,}\) we need \(a_y\text{,}\) which can be obtained from \(y\)-component of centripetal acceleration \(a_c\text{,}\) which we already foubnd in (C), and tangential acceleration \(a_t\text{.}\) Since CM is moving in a circle with angular acceleration \(\alpha\) and radius \(L/2\text{,}\) \(a_t\) will be
Now, we get \(a_y\) by adding the \(y\)-components of \(a_c\) and \(a_t\text{.}\)
We can now set up \(F_y = m a_y\text{.}\) With the axes in Figure 3.2.2 we get
Therefore,
Hence (D) is correct.
Problem 3.2.3. Q2. Motion of Coupled Systems.
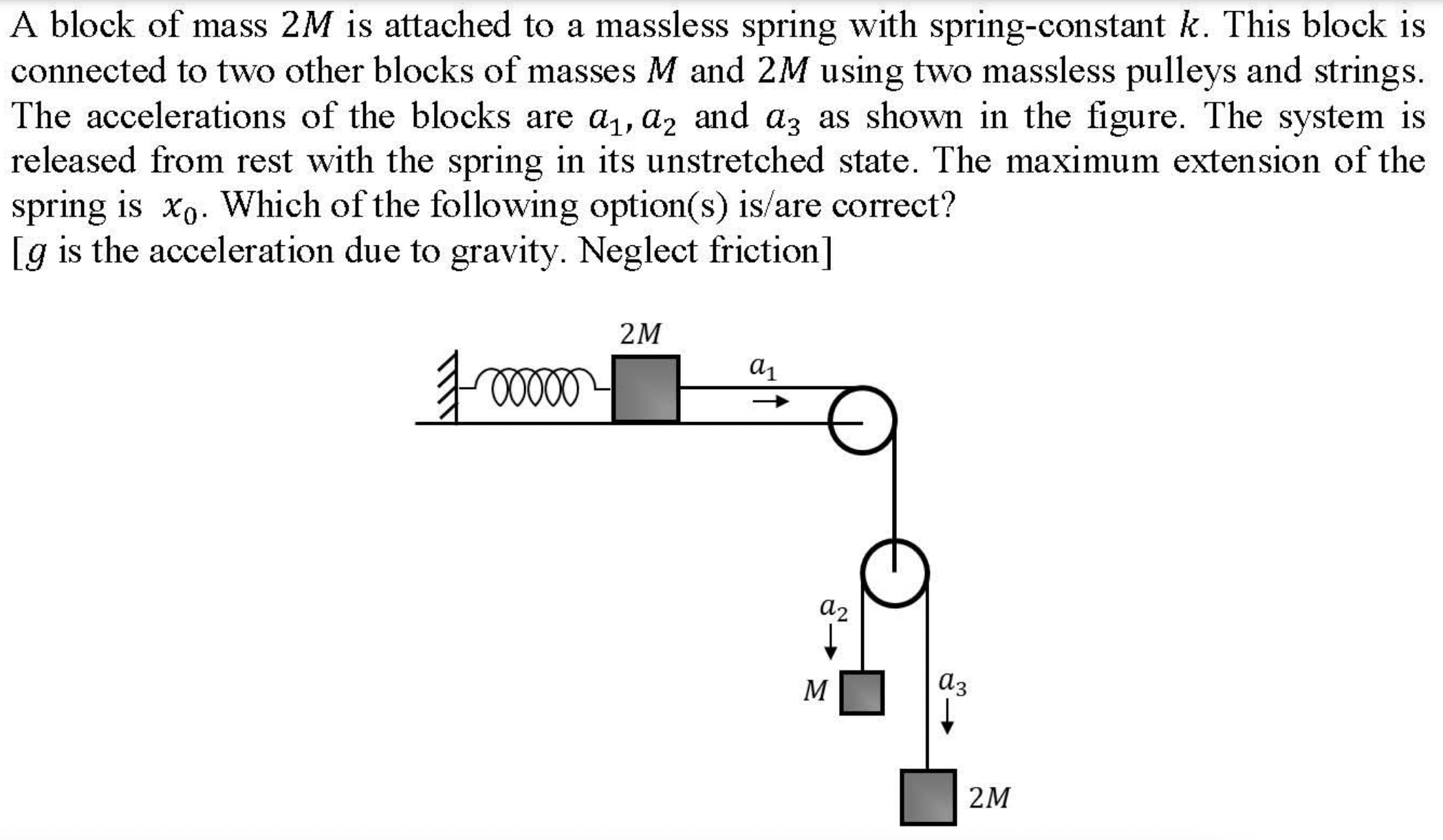
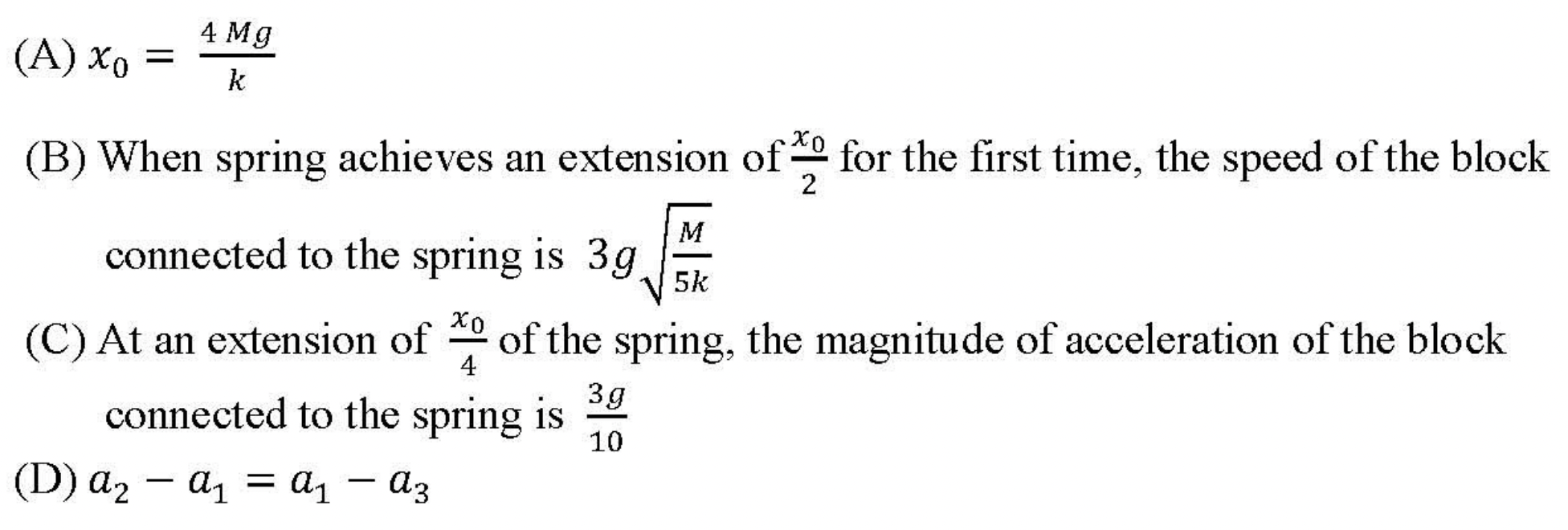
Use constraint in string that goes over the pulley and find acceleration of the block attached to the spring in terms of its position.
(D).
(A): Figure 3.2.4 shows diagram of the problem, where, for convenience, I have made everything along \(x\)-axis. Since the string connecting 2 and 3 has fixed length we have the following constraint.
One time derivative will give
and two time derivatives will give the following relation among accelerations.
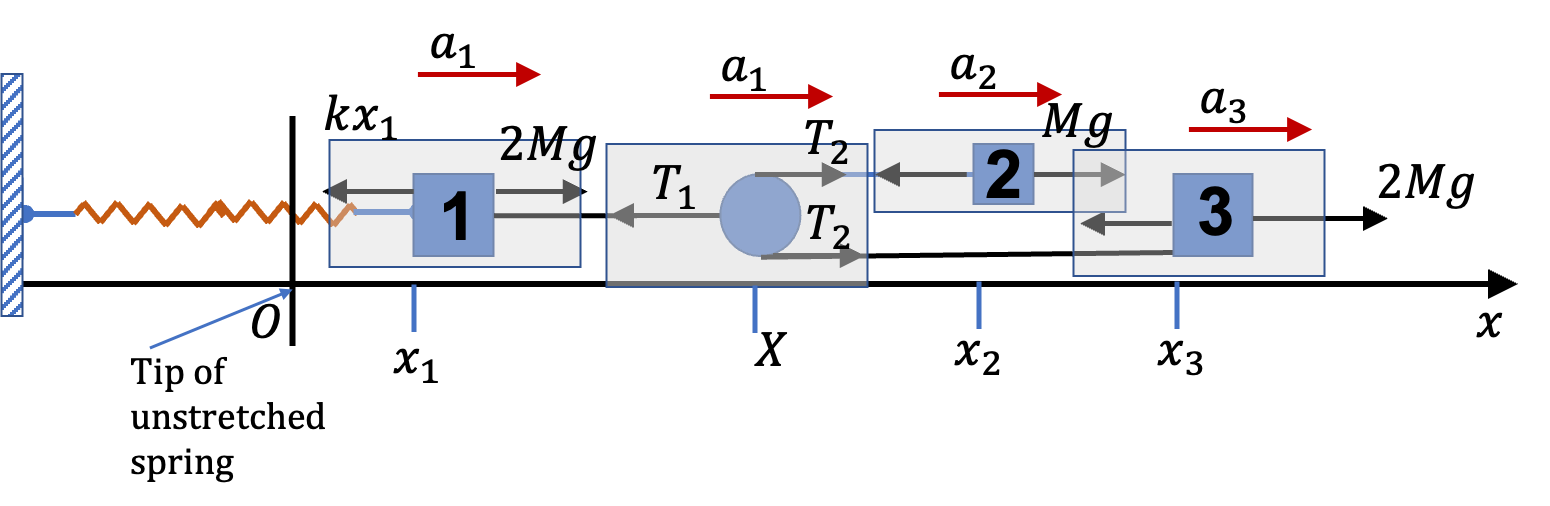
We also choose origin of the corrdinate at the point when the spring is unstretched. Therefore, we will get the following \(x\)-equations of motion.
From last two equations, we can get
which upon using Eq. (3.2.3) and Eq. (3.2.5) gives
which can be written as
Subtracting this to Eq. (3.2.4) to obtain
where
That is
To solve this equation, let us introduce simplifying constants.
Then, this is
Let \(y = x_1 - b\text{,}\) then, we have
which has general solution,
Writing this back in \(x_1\) we have
from which we have velocity
Now, we use the initial condition of rest and position given in the problem, which trtanslates to
Thus, we get
Hence, the motion of block 1 is given by
where \(b\) and \(\omega\) are given in Eq. (3.2.8). Since \(x_1\) is equal to the stretch of the spring, maximum of the stretch will occur when \(\cos(\omega t)=-1\text{.}\)
Comparing this to the given answer we find (A) given is incorrect.
(B): What's \(v_1\) when \(x_1 = x_0/2\text{?}\) At this time we find
Hence, \(v_1\) at this instant \(\sin(\omega t) = \pm 1\text{.}\) For first pass, the block is moving to right, so we want \(v_1>0\text{.}\)
which is not equal to given expression. So, (B) is incorrect.
(C): From the expression \(a_1 = - \omega^2 (x_1 - b)\text{,}\) we can immediately check this answer.
The answer given is therefore incorrect.
(D): This is already found to be true in Eq. (3.2.3) when we used constraint on the string that goes over the pulley.
Problem 3.2.5. Q3. Collision of a Particle with a Moving Piston.


Head-on elastic collision with massive objects gives \(|v_\text{rel}| = |v'_\text{rel}| \text{.}\)
(B), (D).
(A) In roundtrip of particle, distance trtavelled will be \(2L-V\Delta t\text{,}\) where \(\Delta t\) is time for the trip. Speed \(v\) of the particle will be constant between collisions with the the moving piston. Time \(\Delta t\) will be
Since \(V\ll v\text{,}\) time between collisions with the moving piston will be
Therefore, rate of collision with the moving piston will be
So, the given answer is incorrect.
(B): Let \(v'\) be speed of the particle after a collision with the moving piston and \(v\) speed before the collision. Then, we have
Therefore, change in speed as a result of collision with the moving piston will be
Therefore (B) is correct.
(C): From (A), we have \(\Delta t = 2L/v\) between collisions and from (B) change in speed of the particle equals \(\Delta v = 2V\text{.}\) Therefore,
In time \(\Delta t\text{,}\) piston moves a distance \(|\Delta L| = V\Delta t\text{.}\) Therefore,
This says that given answer (C) is incorrect.
(D) We can write Eq. (3.2.13), for arbitrary length tube. Use \(x\)-axis point to the right and \(x\) be coordinate of moving piston at some instant. Then, for infinitesimal movement of piston, this equation would be
Moving \(v\) to the left and integrating we get
Therefore,
From the given data we get
Therefore, kinetic energy changes by a factor:
Hence, (D) is correct.
Problem 3.2.6. Q4. Electric Dipole Fixed in a Uniform Electric Field.
Use superposition of potential from dipole and external field.
(A)
It is easy to check answers directly rather than derive them from first princiles. We will need following formulas. (Here \(k = 1/4\pi\epsilon_0\text{.}\))
Here \(\theta\) is the angle of a field point with respect to the direction of the dipole.
(A) Net potential at any point of the circle will be
Therefore, the following must be true for all radial directions \(\hat r\text{.}\)
Therefore, direction of \(\vec E_0\) is exactly opposite of \(\vec p\) and magnitude-wise
That is (A) is correct.
(B) Net electric field at A will be (since \(\theta=0\) in the dipole field formula )
Using the result from part (A) above, i.e. \(k p_0/R^3 = E_0 \text{,}\) net electric field will be
At point A, the radial unit vector is
Therefore, field at A is
This is not equal to the given answer. GHence (B) is incorrect.
(C) When you draw field lines of the dipole at B, it is in the same direction as the field \(\vec E_0\) as shown in Figure 3.2.7 , hence, electric field is not zero there. Hence, (C) is wrong. Another way to see this is that \(\theta = 90^\circ\) for point P with respect to the direction of the dipole.
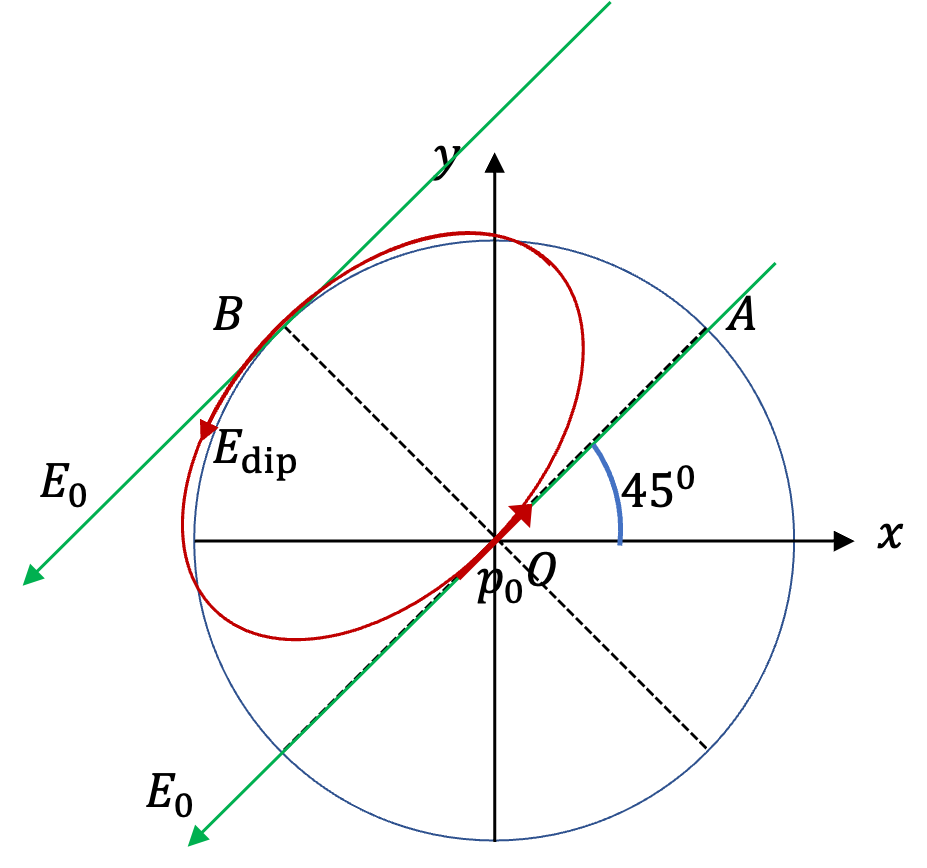
At B \(\hat r\) and \(\hat \theta\) are
Therefore, field at B will be
This is clearly not zero.
(D) Electric fields at A and B are different. That means, field is not same at all points of the circle. Hence, given (D) is incorrect.
I will use Figure 3.2.8 for this problem. Here, external uniform electric field is at an unknown angle \(\theta_0\) and dipole direction \(OA\) is at \(45^\circ\) with respect to \(x\)-axis. We also label an arbitrary point P on the circle with coordinates \((x,y)\) and \((R,\theta)\text{.}\)
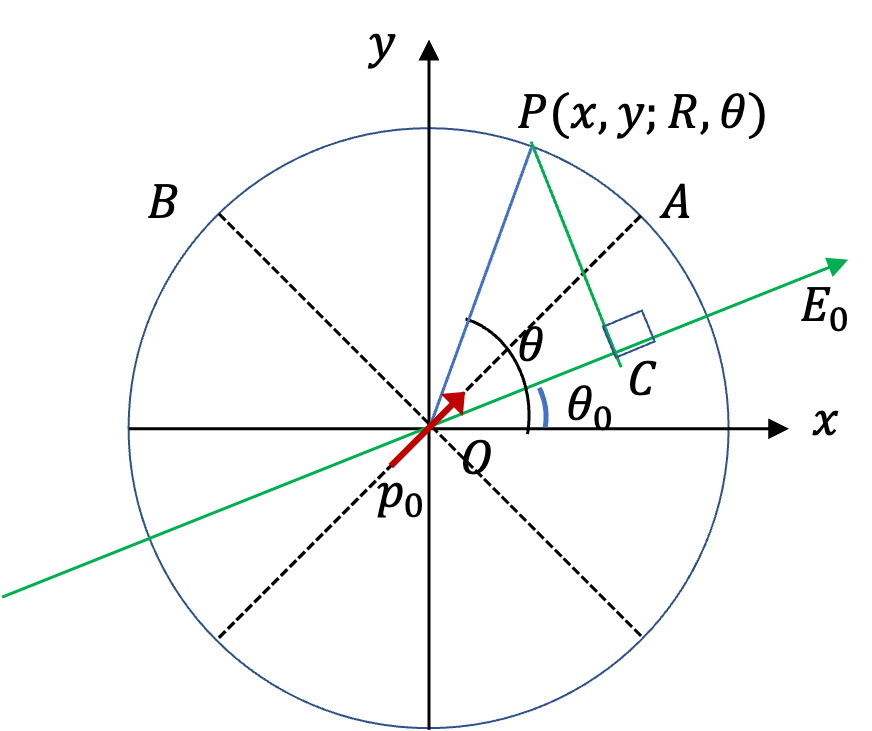
(A): Here we require that potential at all points of the circle be same. That means potential at P must be independent of angle \(\theta\text{.}\) Potential at P is a superposition of potential by the dipole and the potential by the external electric field. With \(p\) magnitude of dipole, which is given as \(p_0\) in the problem.
Potential by external uniform electric field will be written with respect to its value at O. This will be
Therefore, net potential at P will be
Now, this is suposed to be independent of \(\theta\text{.}\) That will happen if following two conditions hold.
From the second equation, we get
That is (A) is correct.
From the first equation, we get
That is external electric field is pointed in the third quadtant, in the direction exactly opposite the direction of the dipole at the origin.
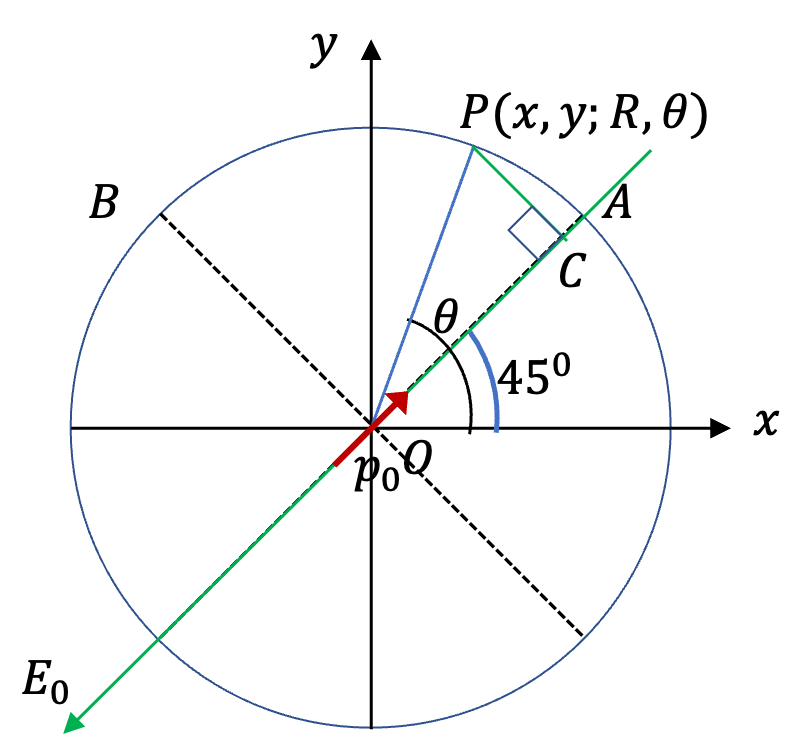
(B): Electric field at point A will be a vector sum of that of dipole and the uniform external electric field.
Although it is easier to work in polar coordinates, I will work in Cartesian coordinates. From \(V_\text{dip}\text{,}\) we immediately get elewctric field.
Let's work out \(x\)-component and guess \(y\)-component from symmetry. I will use \(r\) for \(\sqrt{x^2 + y^2}\text{.}\)
Evaluating this for coordinates of point A, \(x=y=R/\sqrt{2}\text{,}\) and using results of Question (A) above, we get
From Eq. (3.2.16), we can see that \(x\rightarrow y\) will give \(E_y\text{.}\)
At point A, this will evaluate to
To these we add the field \(E_0\) vectorially, giving net electric field at point A to be
This means given answer for (B) is incorrect.
(C): At point B, electric field of the uniform field as same as before, but that of the dipole will be obtained by setting \(x=-R/\sqrt{2}, y = R/\sqrt{2}\) in Eqs (3.2.16) and (3.2.17).
A similar calculation or a symmetry argument will show that
Therefore, net electric field at point B will be
This says that given (C) is incorrect.
(D): From answers for electric field at points A and B, we already know that electric field does not has same magnitude at A and B. Hence, its not same at all points of the circle. Therefore, given (D) is incorrect.
Problem 3.2.10. Q5. A Mixture of Monatomic and Diatomic Ideal Gases Compressed Adiabatically.


You need to know equivalent degrees of freedom.
(A), (C), (D).
This problem requires you to know that in an ideal gas mixture, you deal with equivalent degrees of freedom, \(df_\text{eq}\text{.}\) For a mixture of \(k\) ideal gases, this is given by
Degree of freedom of a single ideal gas depends on translational, rotational, and vibrational degrees of freedom. For monatomic gases, you only have three degrees of freedom, for diatomic gases, you will have two rotational and one vibrational degrees on top of that. Here, the diatomic gas is rigid, so, you don't have vibration for that. Thus, in the given problem we have
The adiabatic gas constant of the mixture will
(A): In an adiabatic process, no heat is exchanged. That means work done will equal change in internal energy.
where \(T_f\) is the final temperature and \(T_i = T_0\text{.}\) To find \(T_f\) we emake use of the given information of volume in
Thus,
Therefore,
That is (A) is correct.
(B): To check this, we note that \(U_f\) is all in kinetic energy.
which is not in the range of answers given. GHence, (B) is incorrect.
(C): We already know \(T_f\) and \(V_f\text{,}\) hence,
This is in the range given. Hence, (C) is correct.
(D): We already calculated \(\gamma_\text{eq} = 1.6\text{.}\) This is correct.
Problem 3.2.11. Q6. Apparent Depth for Flat and Curved Interfaces.
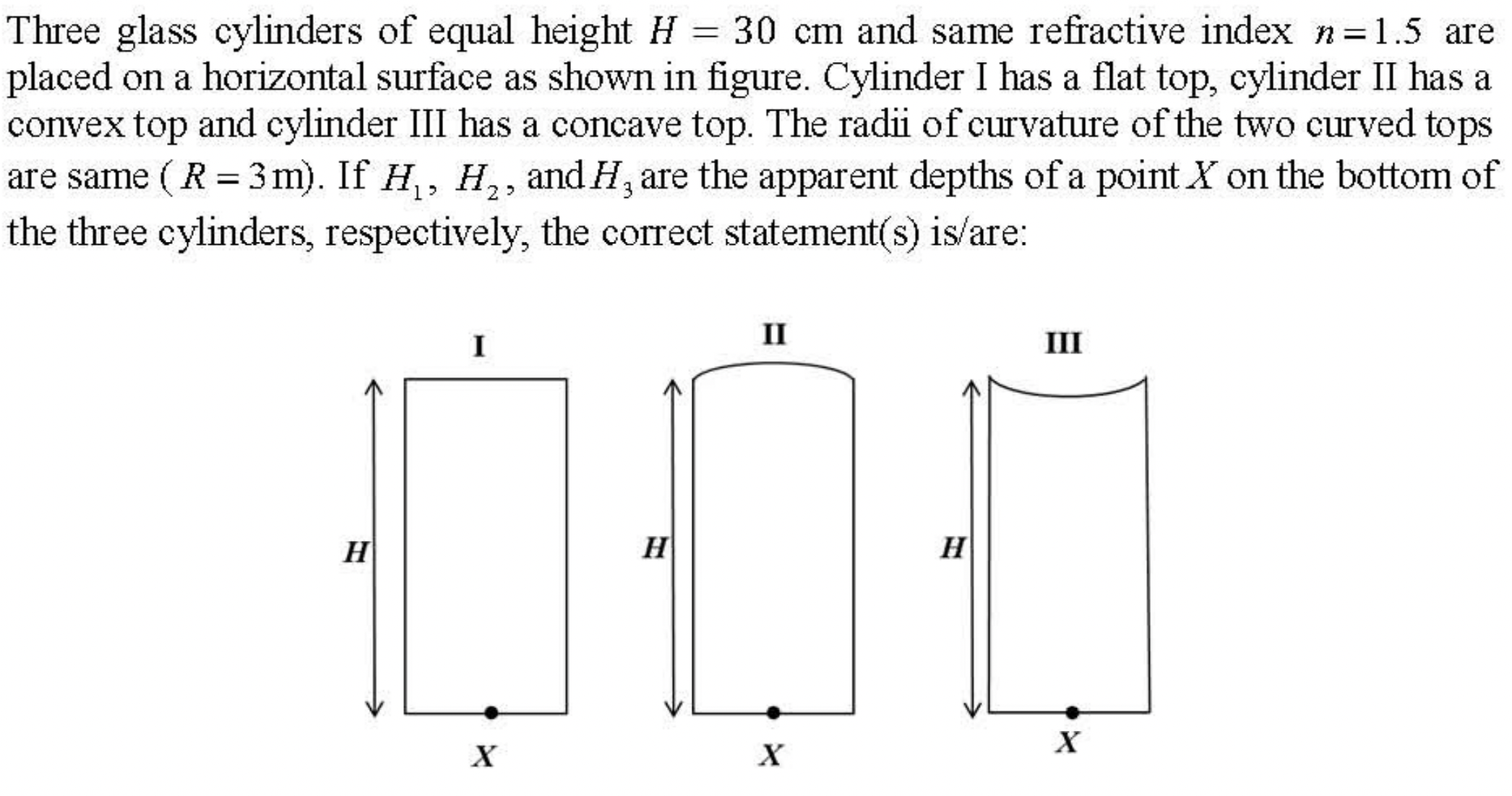

Use \(\frac{n_1}{p} + \frac{n_2}{q} = \frac{n_2 - n_1}{R}\text{.}\)
(A), (C).
You need to work with image formation by refraction at an \(n_1/n_2\) interface, whose formula is
whith sign convention \(R \lt 0\) if center of the curvature of the interface is in medium \(n_1\) and \(R \gt 0\) if in medium \(n_2\text{.}\) For plane interace, \(R=\infty\text{.}\) All distances are from the interface.
We find \(q\) for the three cases. They are called \(H_1\text{,}\) \(H_2\text{,}\) and \(H_3\) respectively if they fall in medium \(n_1\text{.}\) We have been given that \(p=0.3\text{ m}\) and \(|R|=3\text{ m}\text{.}\) Hence
Thus, we find that
(A): \(H_2 \gt H_1 \) is correct.
(B): \(H_3 \gt H_1 \) is incorrect.
(C): \(H_2 \gt H_3 \) is correct.
(D): \(H_2 - H_1 = 0.207 - 0.20 = 0.007 \text{ m} = 0.7\text{ cm}\) is not between \(0.8\text{ cm}\) and \(0.9\text{ cm}\text{.}\) Hence, this is incorrect.
Problem 3.2.12. Q7. Young's Double Slit Experiment.
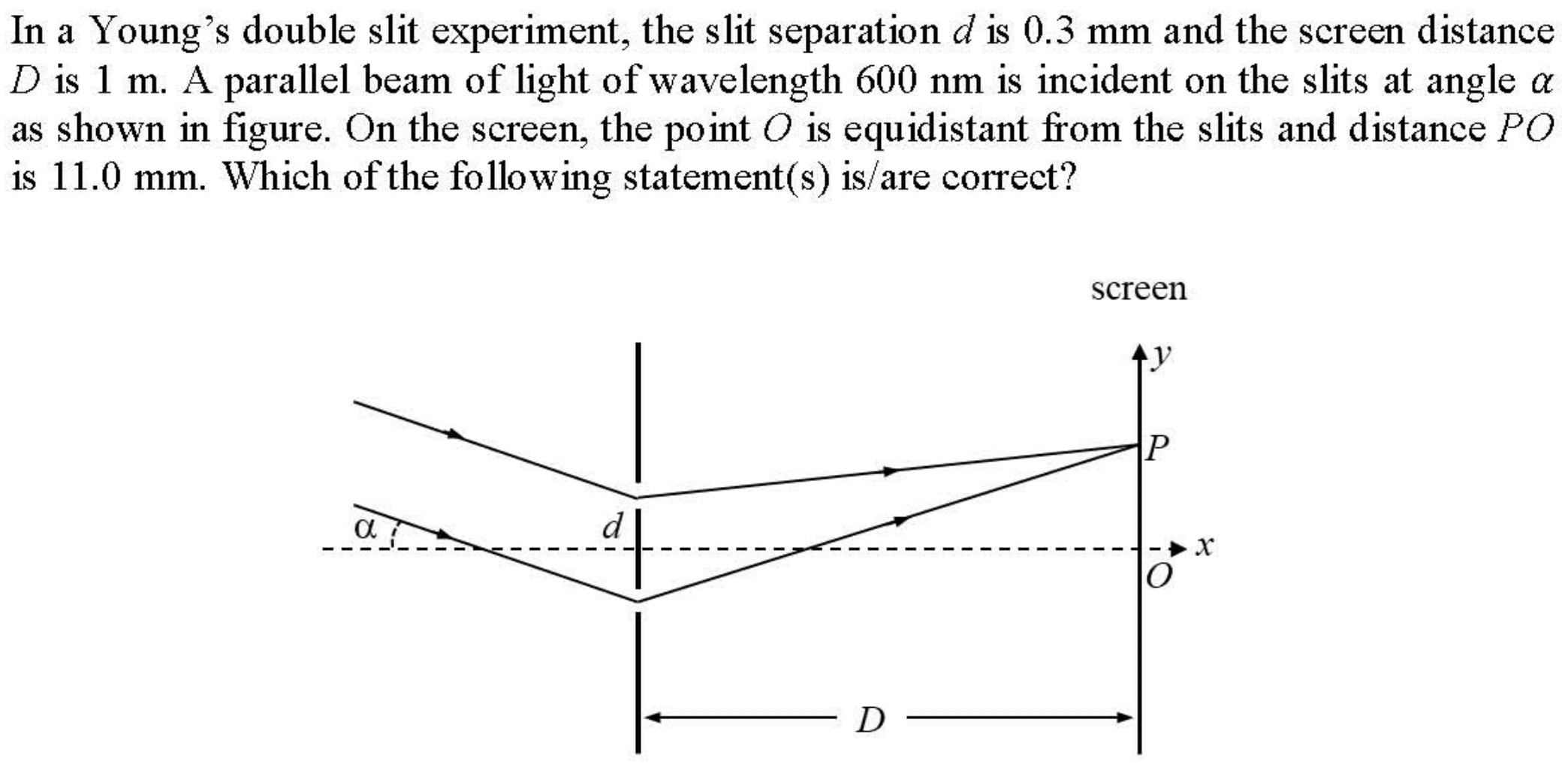

Difference in path will come from both sides of the slit.
(C)
Figure 3.2.13 shows the set up with additinal drawing for difference in the paths through the two slits. The paths through slits \(S_1\) and \(S_2\) starting from wavefront \(XY\) will be the difference of
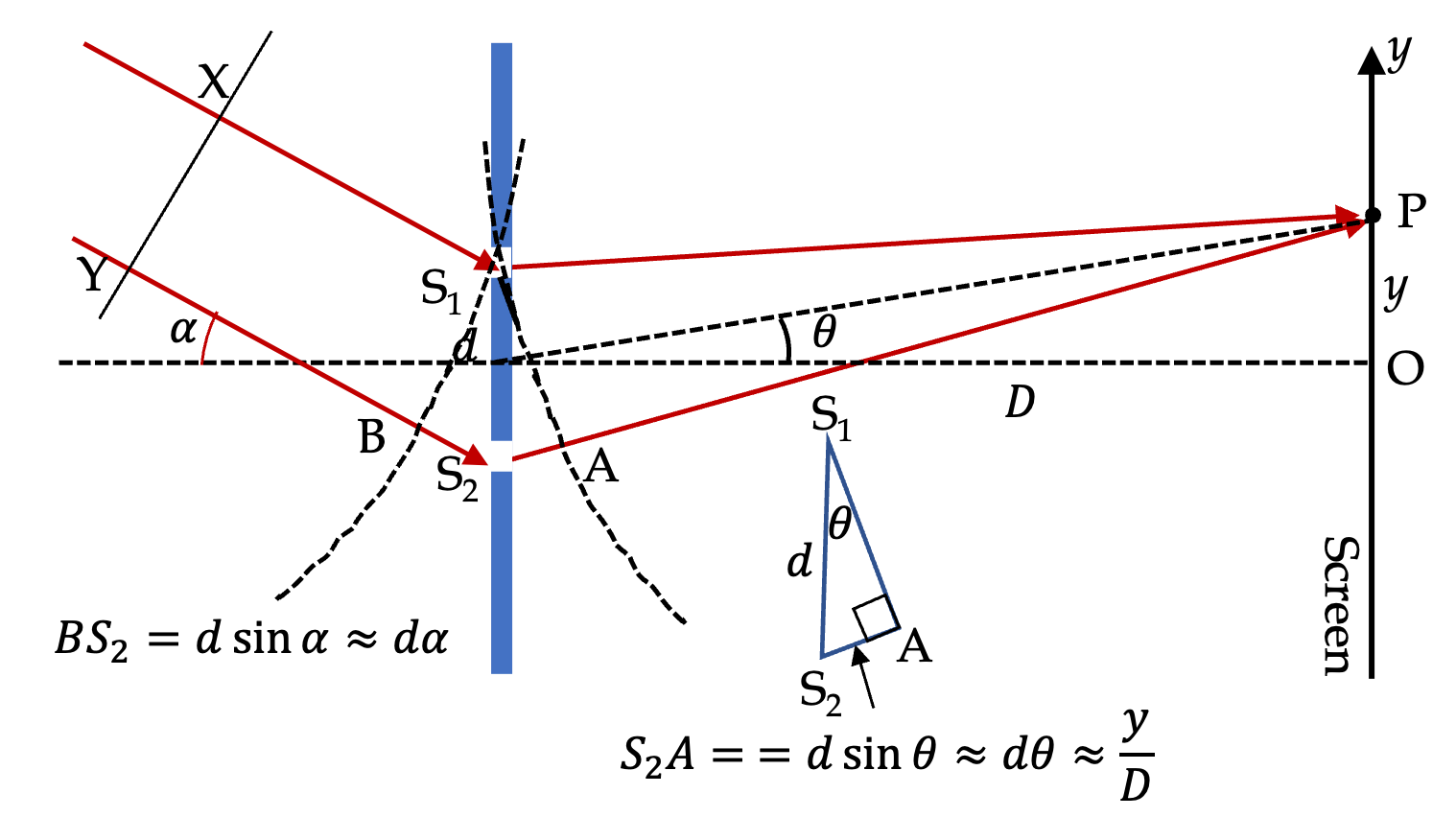
Thus, we will have
For small angles, this will simplify to
Writing \(\tan\theta = y/D\) and \(\tan\alpha \approx \alpha\) we get
For P to be a location of constructive interference will mean that
and for destructive interference,
Both of these can be combined into
with \(a=2\) and \(n\) only odd integer for destructive interference. Now, using numerical values given, we can specialize to the following for \(\alpha = 0.36/\pi = 2/1000\text{ rad}\text{.}\) There is a problem at zero alpha. Let us use a factor \(f = 0 \text{ or } 1\) for this.
where \(y\) is in \(\text{mm}\text{.}\) Now, we are ready to check the answers.
(A): To check if there is a destructive interference at O, we check
Hence, this is not a destructive interference. (A) is incorrect.
(B): Here we need to check
Hence (B) is incorrect.
(C): To check
Hence, it is a destructive interference. Thus, (C) is correct.
(D) To check if fringe spacing will depend on \(\alpha\) we write the formula for \(y\) for a constructive interference. Thus, \(d\left(\alpha + \frac{y}{D} \right) = n \lambda, \ \ (n\ \text{integer})\) can be written as
The separation between fringes \(n\) and \(n+1\) will be
Hence (D) is incorrect.
Problem 3.2.14. Q8. Energy and Momentum Conservation in Electronic Transition of Atoms.


For H-atom energy levels we will need \(E_n = -\frac{13.61\text{ eV}}{n^2}.\)
(A), (D).
For H-atom energy levels we will need
That is \(E_1=-13.61\text{ eV}\) and \(E_4 = -13.61/16 = -0.85\text{ eV}\text{.}\)
(B): From the absorption data we can figure out the wavelength of absorbed photon.
Therefore,
From \(\lambda_a/\lambda_e=1/5\text{,}\) we will get
Thus (B) is incorrect.
(A): Now, we use transition from \(n=4\) to \(n=m\) with emission of \(\lambda_e\) to get \(m\text{.}\)
Hence,
Therefore, \(m=2\text{.}\) Thus (A) is correct.
(D) By equipartition theorem, average \(KE_n =\frac{1}{2}E_n\text{,}\) we can get the ratio of KE in two levels.
Thus (D) is correct.
(C): Finally, we use conservation of momentum to relate the momentum of atom in the two processes by using the values of th momentum of photons absorbed and photons emitted. Thus
Thus (C) is incorrect.
Problem 3.2.15. Q9. Inelastic Bouncing.

Do each bounce and sum.
\(4\text{.}\)
Let's look at the first bounce. During this bounce, average velocity will just equal the \(v_x\text{,}\) since average \(v_y\) will be zero. Magnitude of average velocity is denoted by \(V_1\) here. Hence,
By looking at the vertical motion, we get the time in flight of the first bounce to be
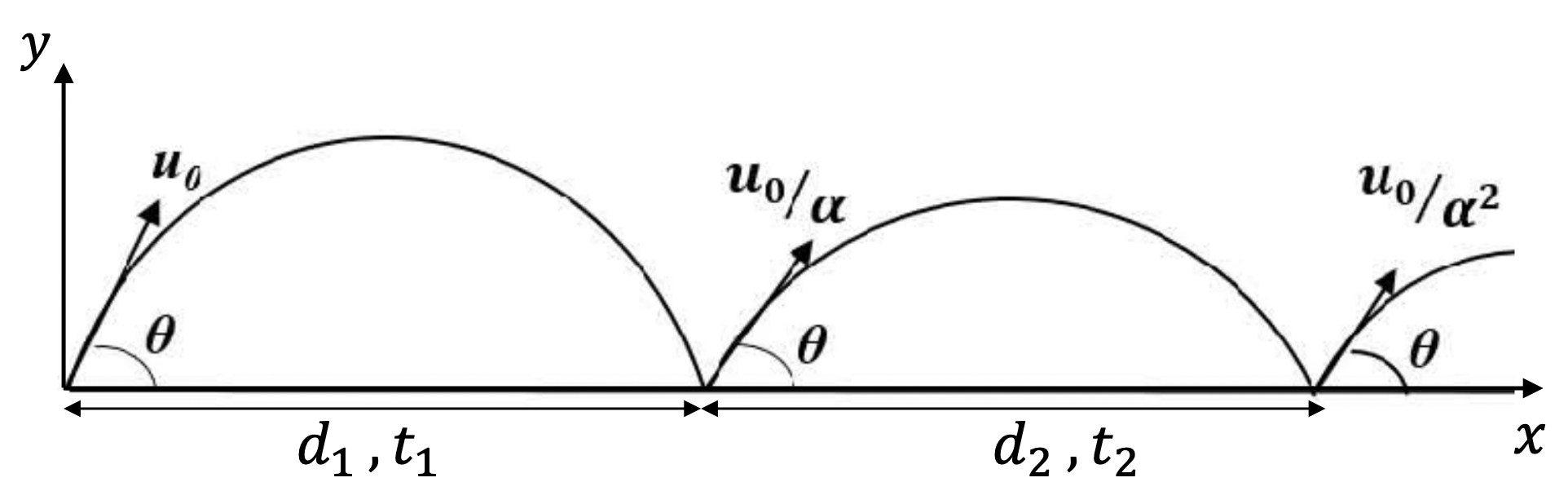
The distance traveled in the first bounce will be
Now, To get these quatities for the \(m^\text{th}\) bounce we just need to replace \(u_0\) by \(u_0/\alpha^{m-1}\text{,}\) where \(\alpha \gt 1\text{.}\)
The total time and total distance will be
Therefore, average velocity for the entire motion will be
Left side is \(0.8 V_1\) and in the right side we replace \(u_0\cos\theta\) by \(V_1\) to get
Hence, \(\alpha = 4\text{.}\)
Problem 3.2.17. Q10. Induced EMF in an RL circuit with a Rod Moving on a Rail.
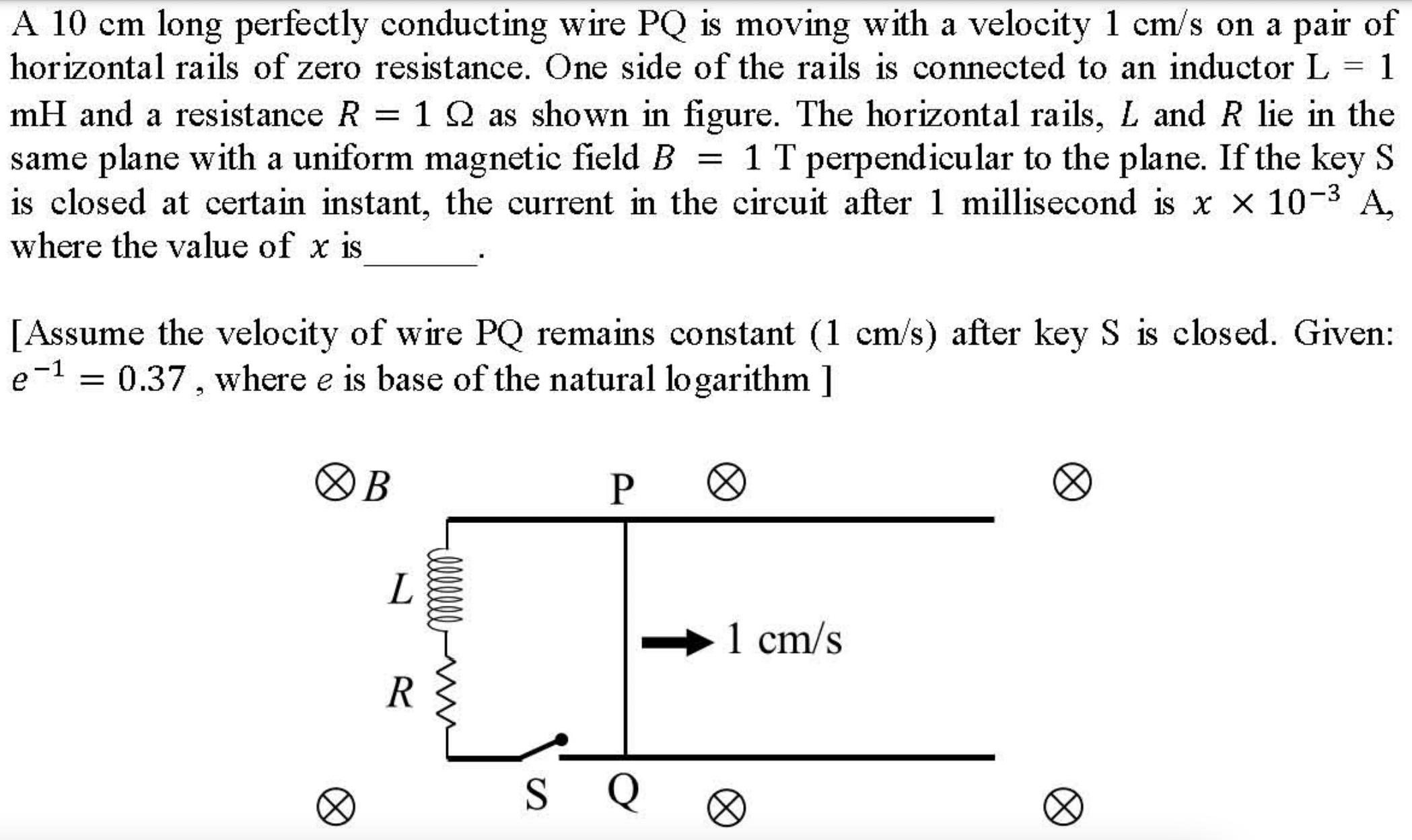
You will need induced EMF for motional EMF, \(\mathcal{E}_\text{ind} = BvL\text{,}\) and \(RL\) circuit with a source.
0.67.
Let \(L=PQ\) and \(v\) speed of the rod PQ. Then, induced EMF in the circuit is
When the rod is moving we have a series \(RL\) circuit with source \(\mathcal{E}_\text{ind}\text{.}\) Equation of motion will be
Solution of this equation is
Numerical values are
Therefore, at \(t=1\text{ ms}\) current is
Hence, answer is 0.67.
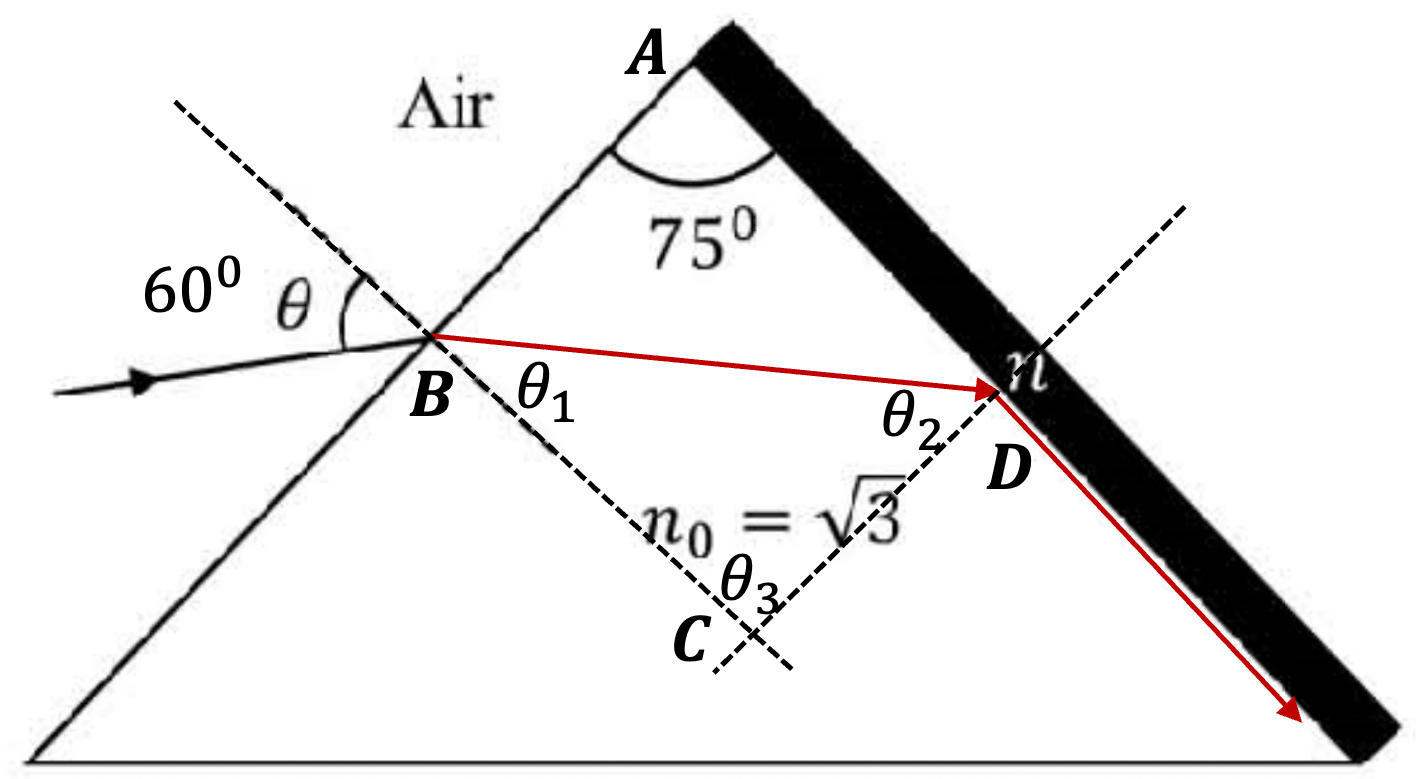
Problem 3.2.18. Q11. Total Internal Reflection in a Coated Prism.
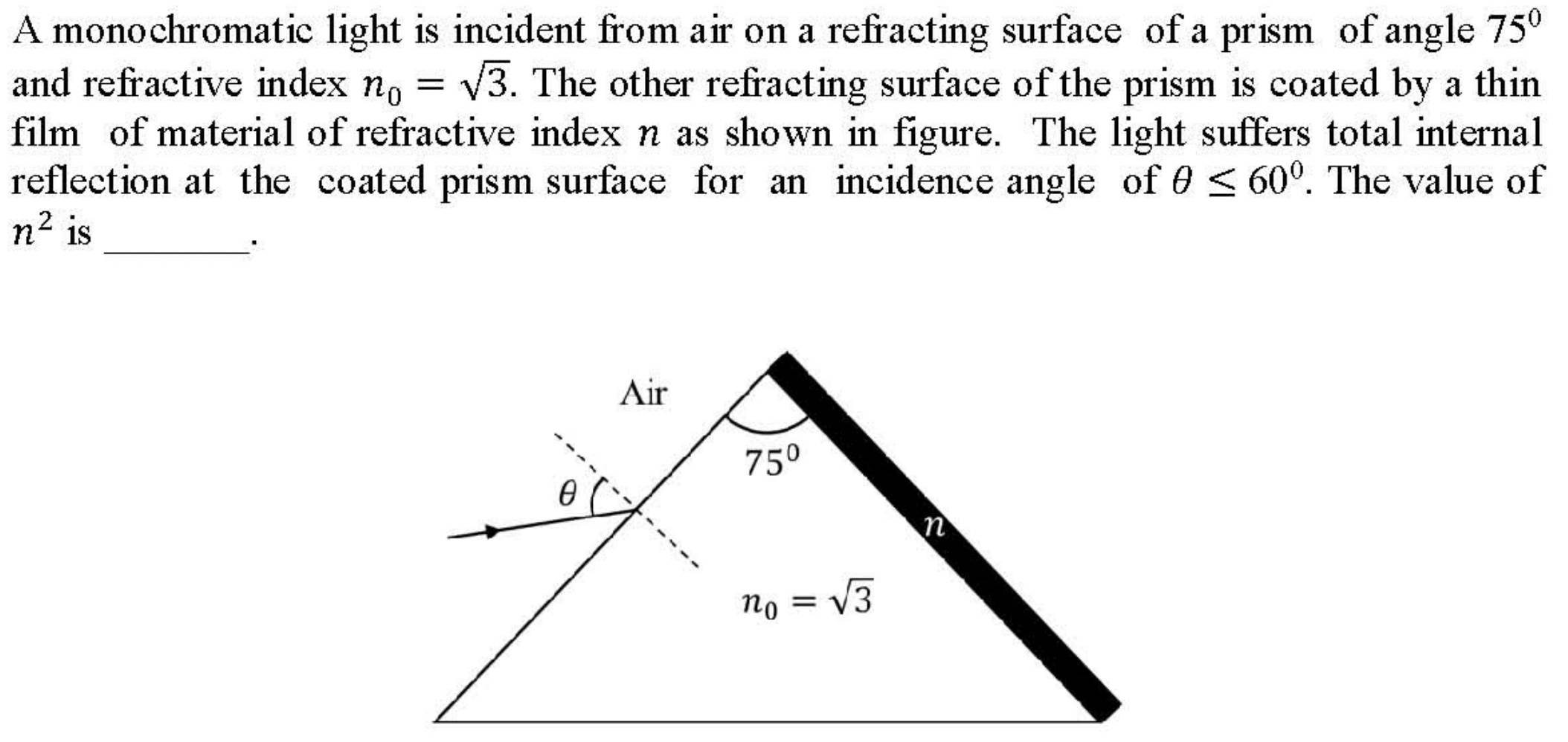
Use incidence angle \(\theta=60^\circ\) and work out the refractions.
1.5
Figure 3.2.19 shows the situation at \(\theta = 60^\circ\text{.}\) At this angle of incidence, the incidence angle at point D is critical angle. Hence
Problem 3.2.20. Q12. Optical Impulse on a Perfectly Reflecting Mirror.
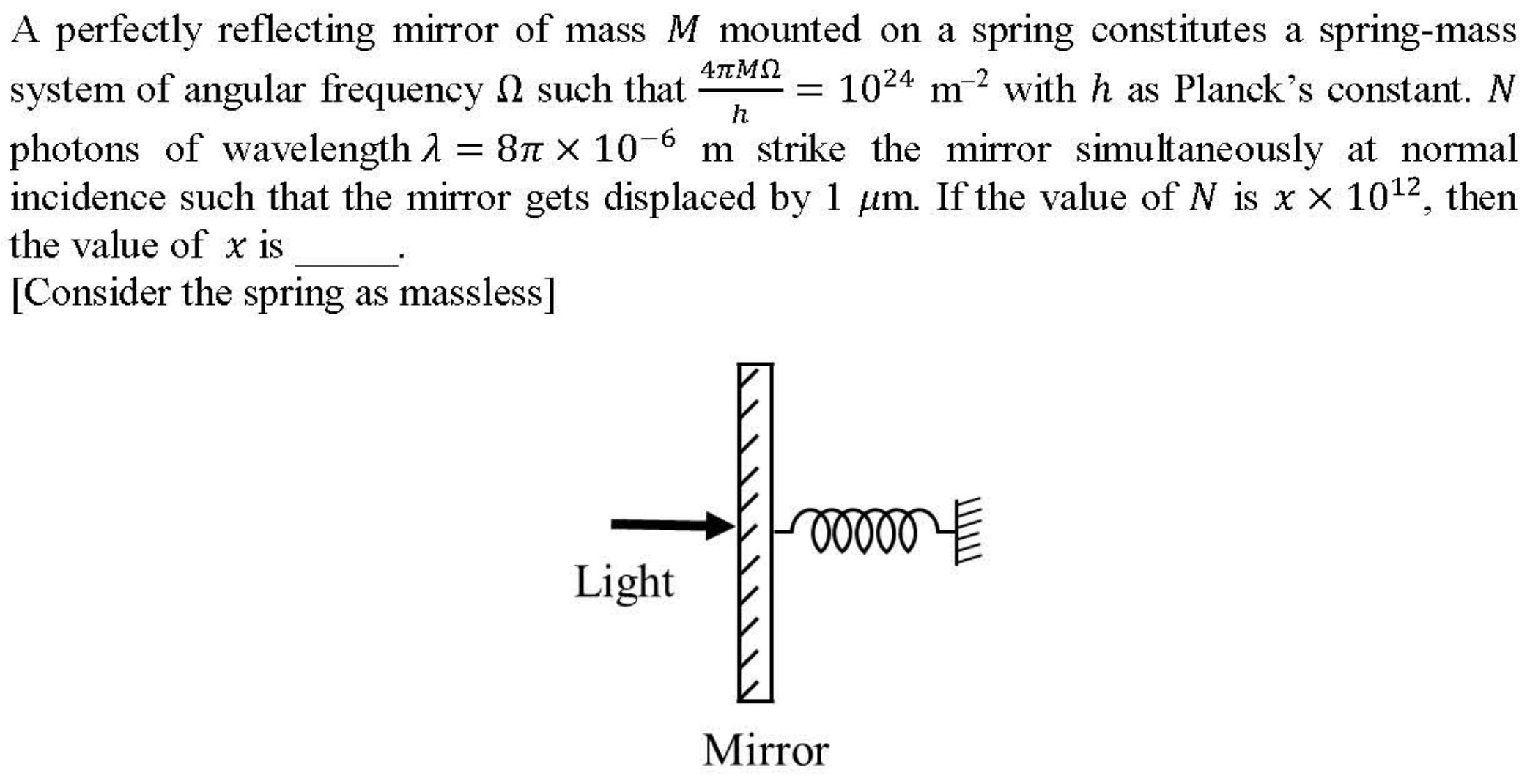
First use conservartion of momentum on the mirror and then use conservation of energy on the spring.
\(x=1\text{.}\)
First we use conservation of momentum on the mirror. Each photon carries a momentum of \(p = h/\lambda\text{.}\) Upon reflection, direction of momentum of photon changes. Therefore, momntum chane of each photon will be
For \(N\) photons, we will get
We are told that \(N= x \times 10^{12}\) and we are to find \(x\text{.}\) Let \(V\) be the resulting velocity of mirror after collision. Then, conservation of momentum in the collision of photons and mirror implies that
Here, we do not know values of \(M\) and \(V\text{.}\) So, we need another condition. That comes from applying energy conservation of mirror/spring system. Kinetic energy in the mirror will end up as potential enery in spring when mirror comes to rest upon compressing the spring. Let \(\Delta l \) denote the compression of the spring.
We know that \(k\) can be replaced by \(M\Omega^2\text{.}\) Therefore, we can write this so that we can use \(M\Omega\) given in the problem.
Canceling out \(1/M\) from both sides, takign square root, and using \(MV\) from conservation of momentum we get
Hence
Hence, \(x=1\text{.}\)
Problem 3.2.21. Q13. Energetics of Alpha and Gamma Decays.

Use energy conservation and momentum conservation in the first equation.
\(135\text{ keV}\text{.}\)
Let \(E^*\) be energy of excitation state compared to ground state of \(Rn\text{.}\) Then, energy of \(\gamma\) is just this energy. From energy consrvation in \(Ra\rightarrow Rn^* + \alpha\) reaction we get
Using \(E_\gamma = E^*\)
We know everything here except \(K_{Rn*}\text{.}\) We use conservation of momentum in the first reaction. Since \(Ra\) is at rest, the momentual of \(Rn*\) will equal in magnitude to that of \(\alpha\text{.}\) Using nonrelativistic relation between momentum and kinetic energy, i.e., \(p=\sqrt{2mK}\) we get
Numerically, we get
Hence, we get the following for energy of gamma.
which is \(135\text{ keV}\text{.}\)
Problem 3.2.22. Q14. Image Formation by a Thin Convex Lens and Precision of a Ruler.

Errors should add in quadrature.
\(0.81\%\text{.}\)
You will need error addition formula. Thus, error in \(z\) in \(z=x+y\) is obtained by quaadrature of errors in the two terms.
Note: \(\Delta z \ne |\Delta x| + |\Delta y|\text{.}\) If you have a product, the error is usually written as fraction. Say, you have \(f = g^a\text{,}\) then
Combining the two rules, we will get for \(u = v^a w^b\) to be
Let \(x\) be the optical axis. We are given the following readings of object, lens, and image locations.
The image and object distance will be \(p = x_L-x_o\) and \(q= x_i-x_L\text{.}\) Therefore, in cm units
Now, formula for focal length \(f\) is
We treat \(p\) and \(q\) as independent variables and get \(\Delta f\) corresponding to \(\Delta p\) and \(\Delta q\) separately.
Therefore,
Numerically, this turns out to be
From \(p\) and \(q\) we have
Therefore,
As percentage it is \(0.81\%\text{.}\)
Problem 3.2.23. Q15 & Q16. Vibration Modes of a String.




(B)
(B)
Let \(f_{x,1}\) denote the fundametal frequency of string x of length \(L_x\text{,}\) mass \(x\mu\text{,}\) and tension \(T_x\text{.}\)
Since all \(L_x=L_0\) and all \(T_x = T_0\) we get
Looking at the possibilities in the answer set, we notice that we need to check for two cases, (1) \(f_{1,1} = 1\) and \(f_{1,1} = 1/2\text{.}\)
Case \(f_{1,1} = 1\text{,}\) i.e., I = P:
Already found (B) to be the answer. Let's check for the other case.
Case \(f_{1,1} = 1/2\text{,}\) i.e., I = Q:
This is not even in the choices. So, we stop here.
Let \(f_{x,n}\) denote the \(n^\text{th}\) harmonic frequency of string x of length \(L_x\text{,}\) mass \(x\mu\text{,}\) and tension \(T_x\text{.}\)
Taking ration with \(f_{1,1}\) and equating that to 1, we get
Solving this for \(T_x/T_1\) we get
Lookig at the possibilities in the answer set, we notice that we need to check for two cases, (1) I = P, and (2) I = T.
Case I = P:
Already found (B) to be the answer. No need to check for the other case.
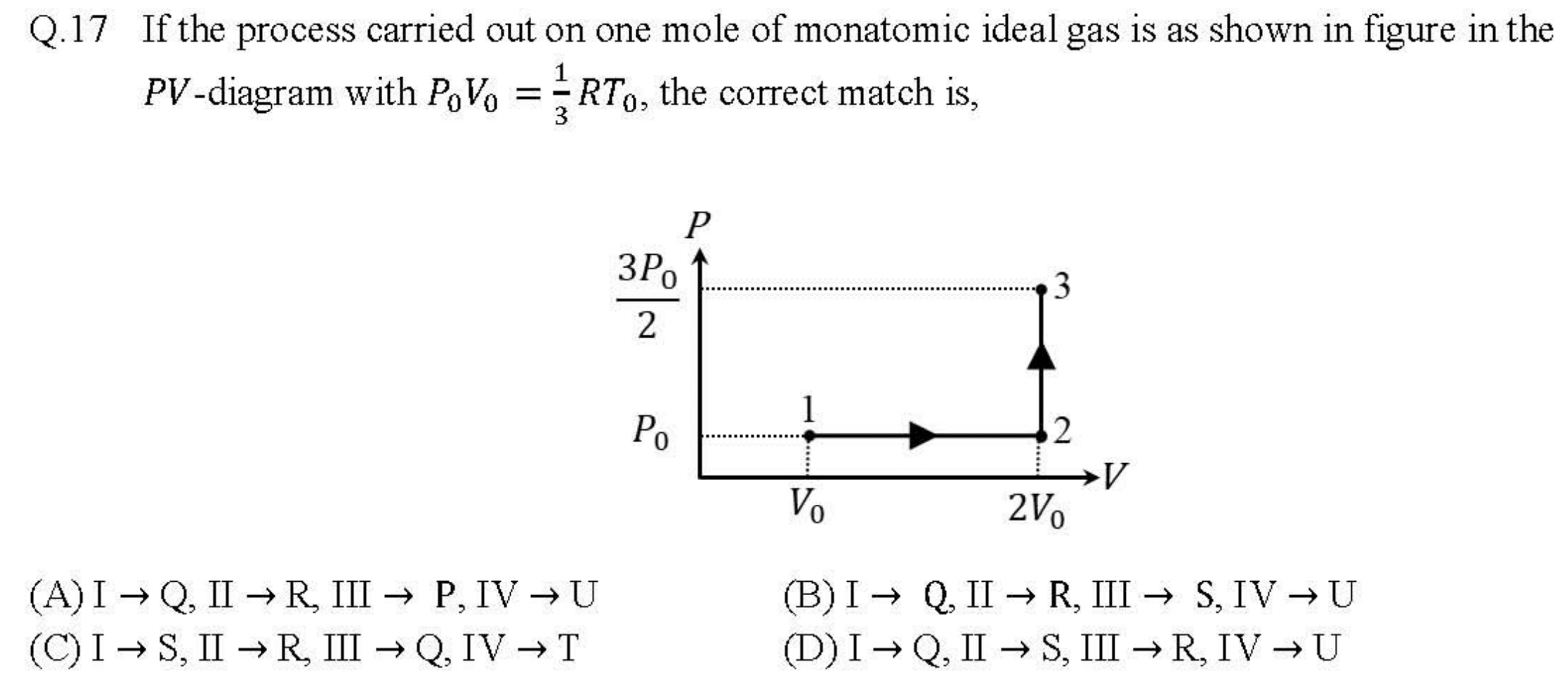
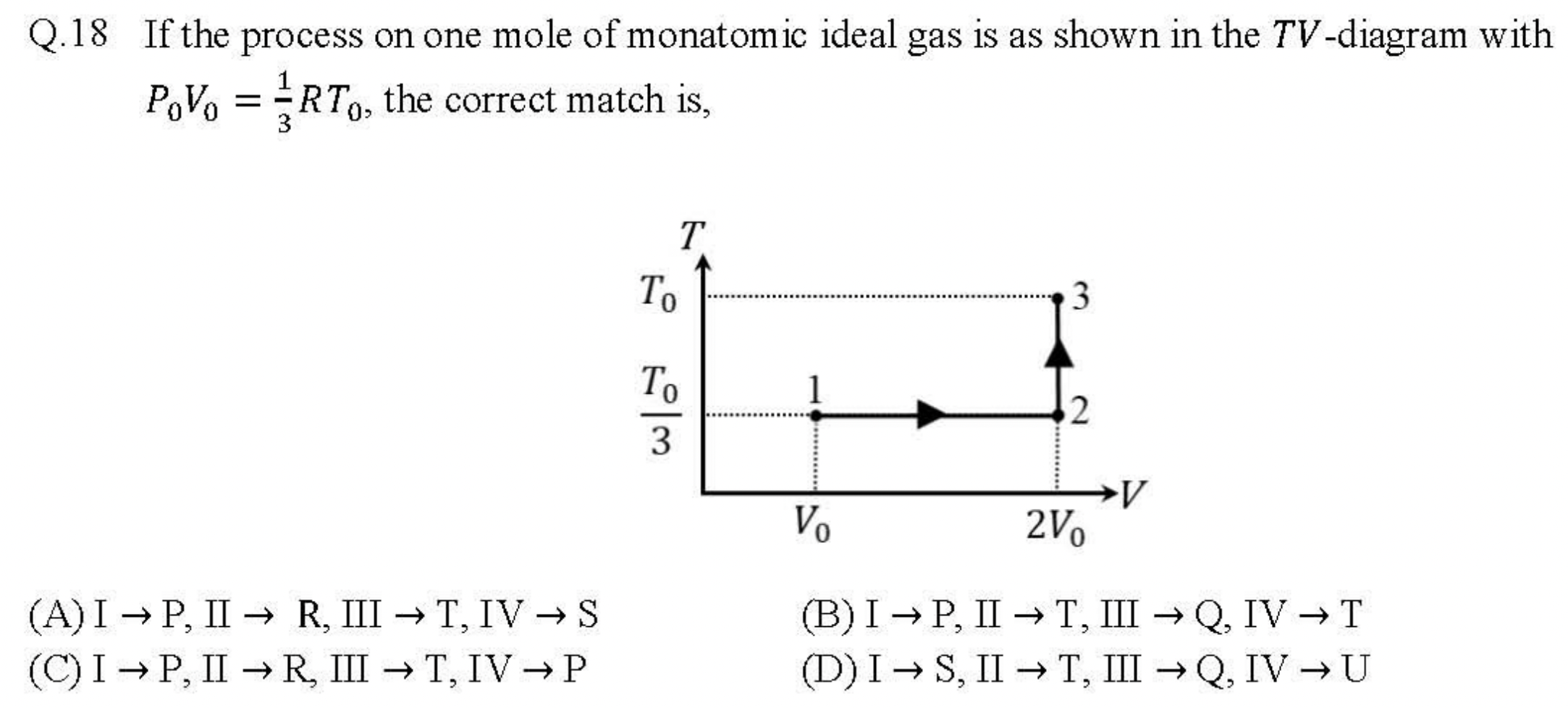
Problem 3.2.24. Q17 & Q18. Thermodynamic Process of an Ideal Gas.


Calculate the quantities asked in the problem.
(B)
(C)
Format of this question is horrible. Looks like we should try to find (I) \(W_{123}\text{,}\) (II) \(U_{13}\text{,}\) (III) \(Q_{123}\text{,}\) (IV) \(Q_{12}\text{,}\) and match against the given answers. You may not need to find all these. Turns out just two of them is enough if you are careful.
We are given that number of moles \(n=1\text{.}\) From \(p_0V_0 = \frac{1}{3}RT_0\text{,}\) this means \(T_1 = T_0/3\text{.}\) Now, let us work out \(W_{123}\text{.}\) We can also just go ahear and get temperatures.
That is (A), (B), or (D). If we calculate (III), we will be done. That is \(Q_{123}\text{.}\)
This means answer is (B). Let's check using II.
This also checks out for (B)
Here \(\text{}\) and \(T_1 = T_0/3\text{.}\) Calculating work and heat in the processes we can resolve the possibilities.
That means (A), (B), or (C). Looks like IV will resolve them.
Hence, the answer is (C). You can double check with II.
This confirms (C).
