Section 2.2 Paper II
Problem 2.2.1. Q1. Apparent Depth in Refraction.
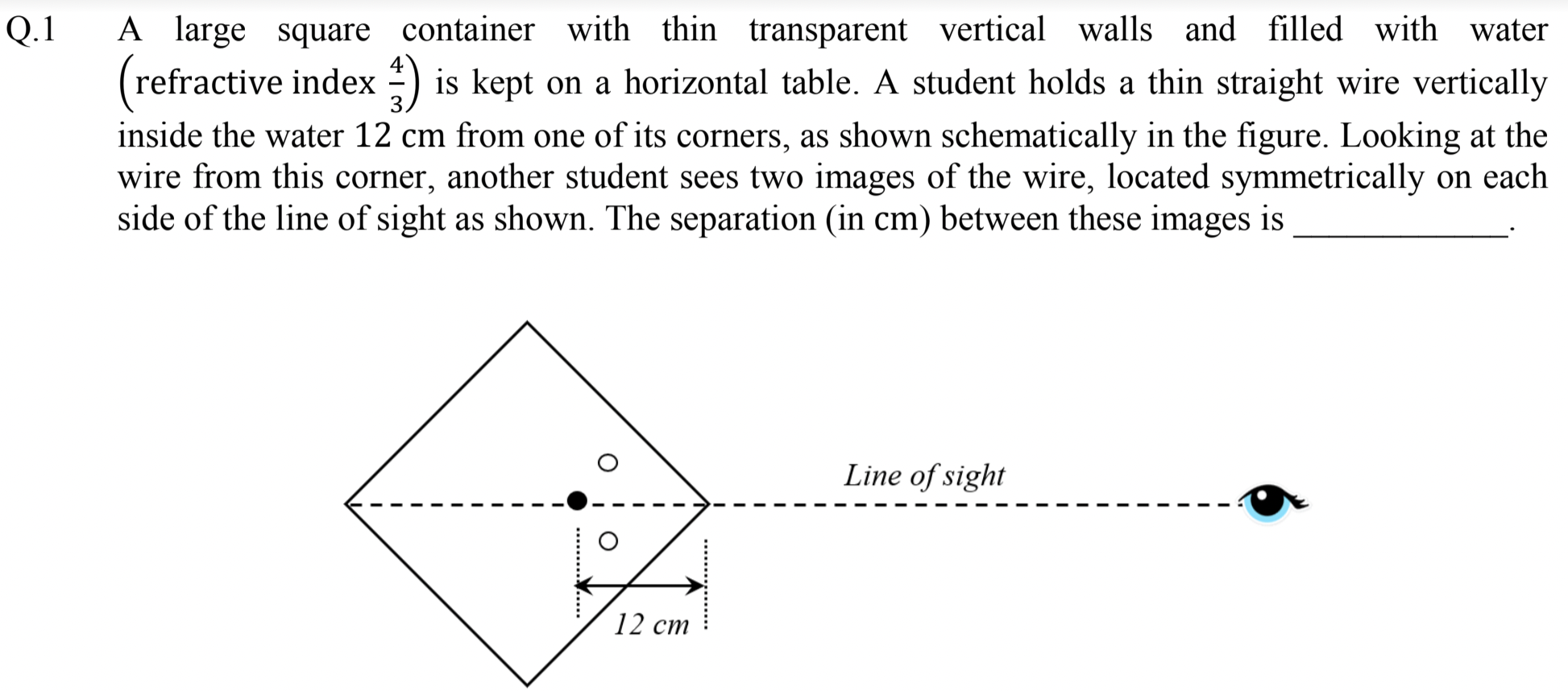
Use Apparent Depth formula for straight ray and then displace for direction of incoming ray from a nearby point.
\(8\text{ cm}\text{.}\)
We use drawing in Figure 2.2.2 to find the answer with assumption that point \(N\) is close to the corner point \(O\text{.}\) In this case, angle of incidence will be
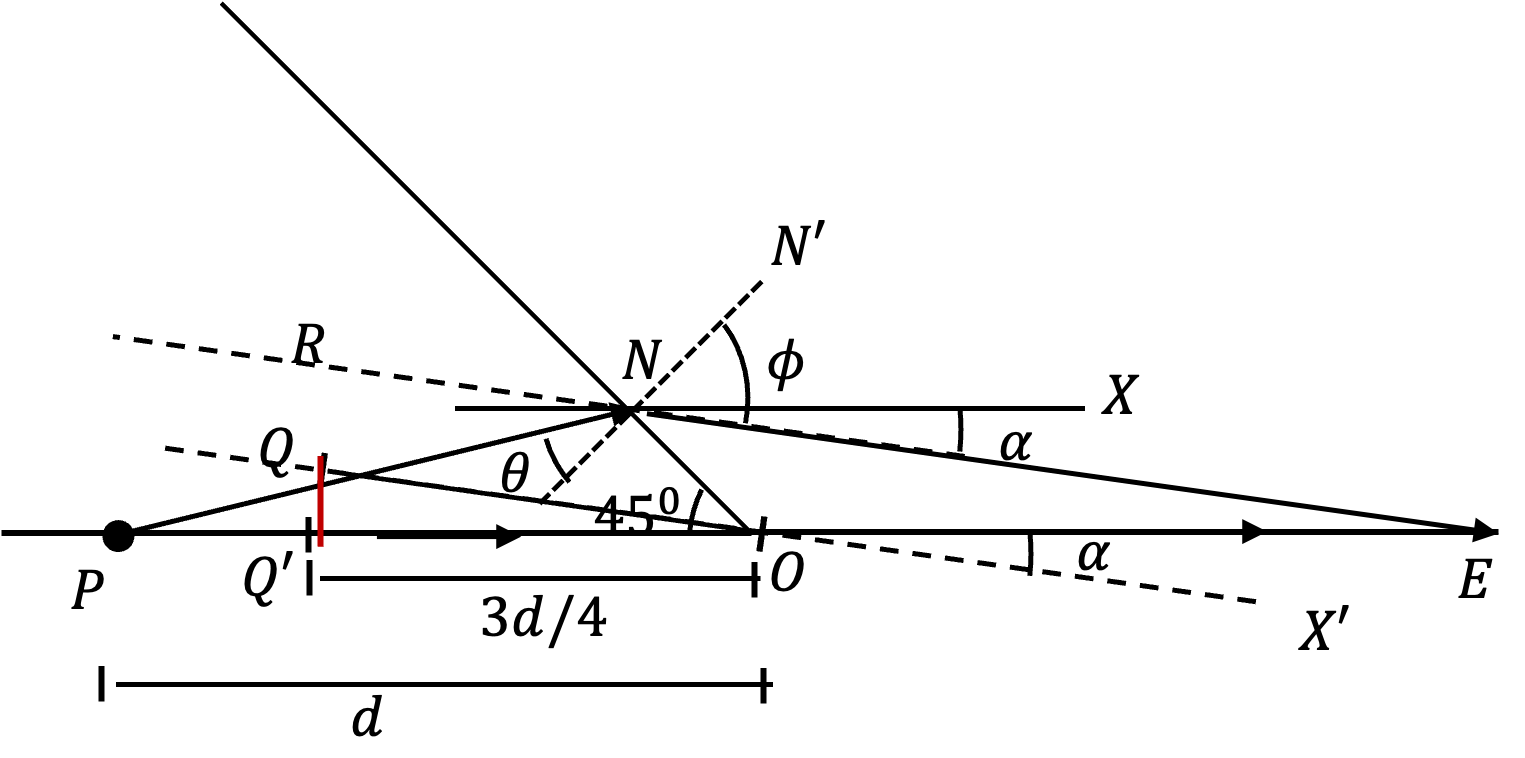
Let \(d = \overline{OP}=12\text{ cm}\text{.}\) Replacing corner point by a vertical plane, we will see the image at \(Q'\) at distance
But since rays from nearby points such a spoint \(N\) will also make into the Eye. One suc ray is shown as \(PN\text{,}\) which refracts in the direction \(NE\text{.}\) This ray makes an angle \(\alpha\) with respect to the horizontal direction. Hence, \(Q'\) from straight-on direction will be displaced in the direction of \(OQ\) and image from rays coming from above horizontal will form at \(Q\text{.}\)
From geometry of figure, we see that
where \(\phi\) is the angle of refraction when incidence angle is \(\theta\approx 45^\circ\text{.}\) Thus,
With \(\overline{OQ}=\overline{OQ'}\text{,}\) we find the vertical distance \(QQ'\) by
Therefore, vertical distance between two images would be \(2\times 3.9 \approx 8\text{ cm}\text{.}\)
Problem 2.2.3. Q2. Bernoulli's Equation.

Use conservation of flow and Bernoulli's equation.
\(N=9\text{.}\)
Figure 2.2.4 shows the flow of air in the train frame of reference.
In this frame, air flows around the train with speed \(v\) with respect to the train while “still air” is actually moving at speed \(v_t\text{,}\) the speed of the train with respect to the ground.

At a point of the tunnel where train has not reached yet, the area of cross-section is \(A_0=4S_t\) and area of cross-section for flow of air around the train is \(A=(4S_t-S_t)= 3S_t\text{.}\) Using conservation of flow, we get
Now, we use this in Bernoulli's equation for the flow.
Therefore,
Hence, answer is \(N=9\text{.}\)
Problem 2.2.5. Q3. Millikan Oil Drop Experiment.
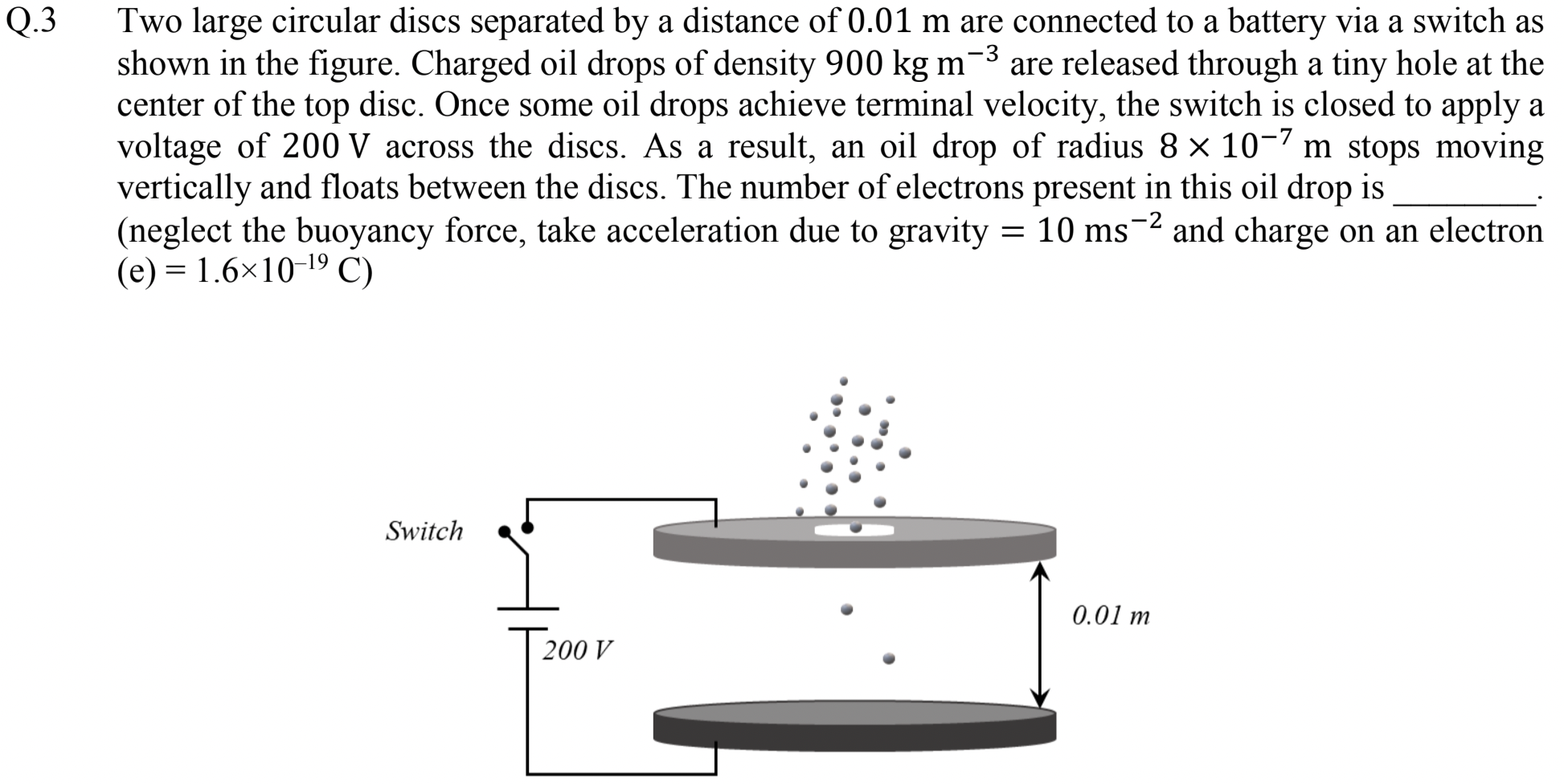
Balance weight by electric force.
\(6\text{.}\)
Since floating droplets have zero velocity, electric force balances weight of the droplet. Let \(N\) be number of excess electrons in a droplet of radius \(r\text{.}\) With electric field \(E=V/d\) between the plates, we will get the following equation when we balance forces on the droplet.
Therefore,
Problem 2.2.6. Q4. Variation of Air Density with Height.
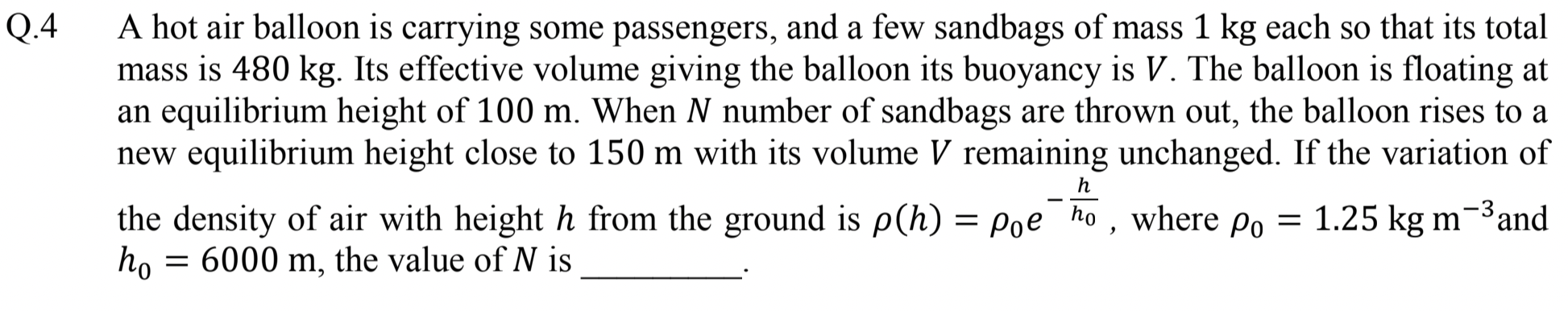
Equate the volume at two heights and use \(e^{-x}\approx 1 - x\) when \(x \ll 1\text{.}\)
\(4\text{.}\)
First we notice that \(h=100\text{ m}\) and \(150\text{ m}\) is much smaller than \(h_0=6000\text{ m}\) in \(\rho=\rho_0 e^{-h/h_0}\text{.}\) Therefore, we will simplify our calculations by using \(e^{-x}\approx 1 - x\) when \(x \ll 1\text{.}\)
Let \(N\) be the number of sandbags that habve been dropped. Let us denote the two densities as \(\rho_{100}\) and \(\rho_{150}\) at heights \(100\text{ m}\) and \(150\text{ m}\text{,}\) respectively. Since volume of the balloon remains same at the two heights, by using \(V = m/\rho\text{,}\) we will get the following equation.
Therefore,
Left side will be \(1 - N/480\text{.}\) Therefore,
Problem 2.2.7. Q5. Potential Energy.
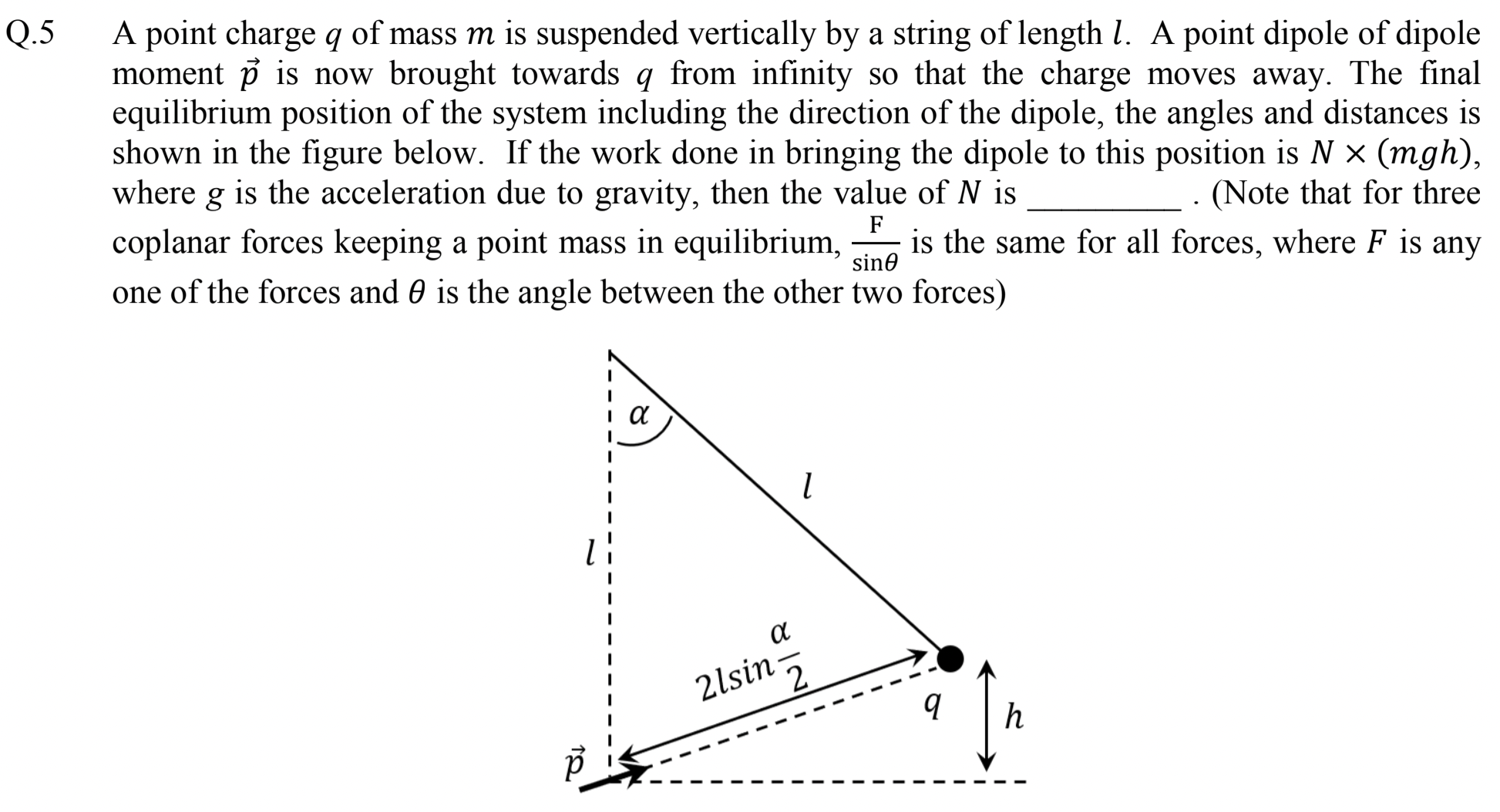
Follow the hint in the problem and work out the angles. Then, use the dipole force to deduce the potential energy due to that force.
\(2 m g h\text{.}\)
My strategy is to find work by the dipole force when we move charge \(q\) from origin, i.e., right at the site of the dipole to the location given in the diagram of the question, while keeping dipole fixed at origin. For this I will implement the hint given in the problem although I could do it some other way.
First we will draw a figure shown in Figure 2.2.8 to define all the angles we will need. From isoscless \(\triangle Opq\text{,}\)
This gives \(\theta_0 = \pi/2 - \alpha/2\text{.}\)
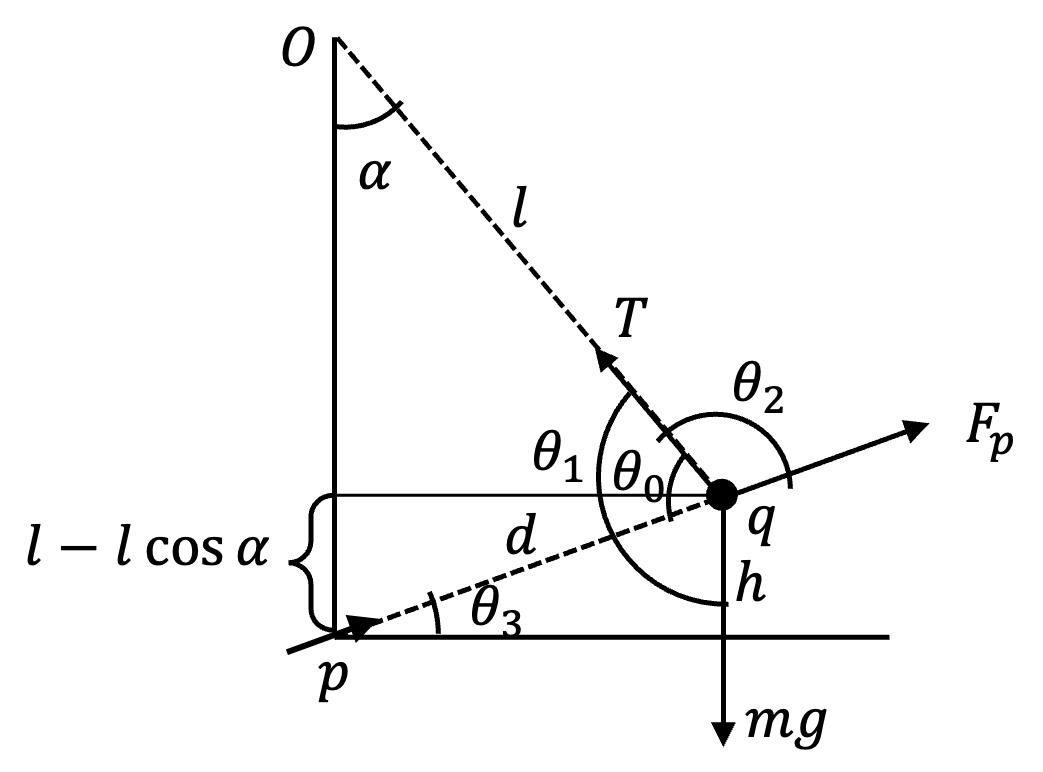
Therefore,
These will give
Now, we can implement equality of \(F/\sin\theta\) for each force in the triplet of coplanaer forces \(F_p,\ T,\ mg\text{.}\) We will get
This gives
We can write this in terms of the distance between the dipole and the charge by multiplying and dividing by \(l\text{.}\)
If charge \(q\) was at an rbitrary distance \(r\) from \(p\text{,}\) force \(F_p\) as a function of \(r\) will be
The direction if this force is from \(p\) to \(q\text{.}\) Then, potential energy due to this force will be
We can rewrite this as
Now, from Figure 2.2.8 you can see that
Hence,
In addition to this potential energy, we have potential energy \(U_g=mgh\) from gravity. Hence, total potential energy will be
Problem 2.2.9. Q6. First Law of Thermodynamics.
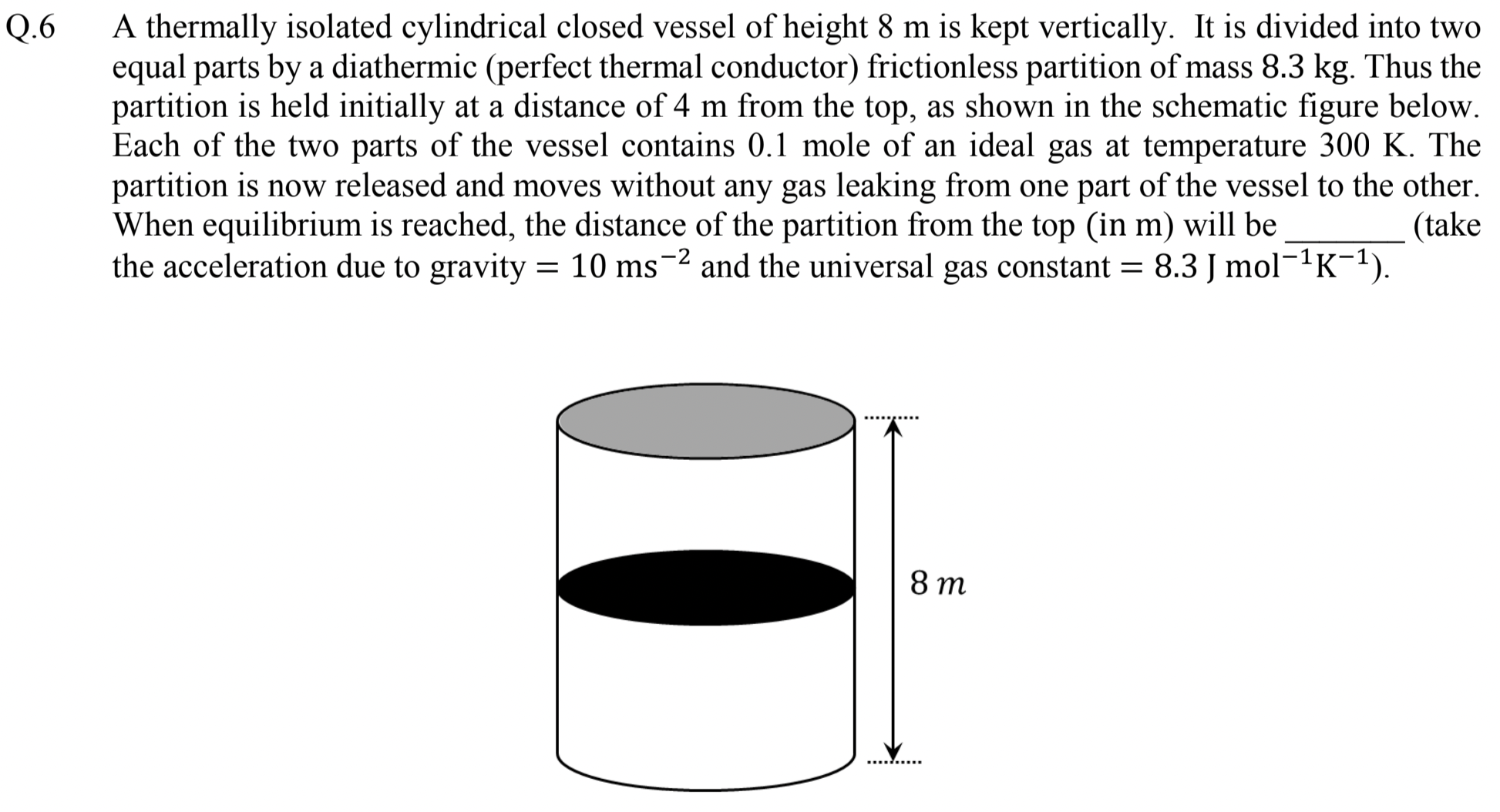
Diathermal piston means final temperature on the two sides will be same.
\(5.78\text{ m} \approx 6\text{ m}\text{.}\)
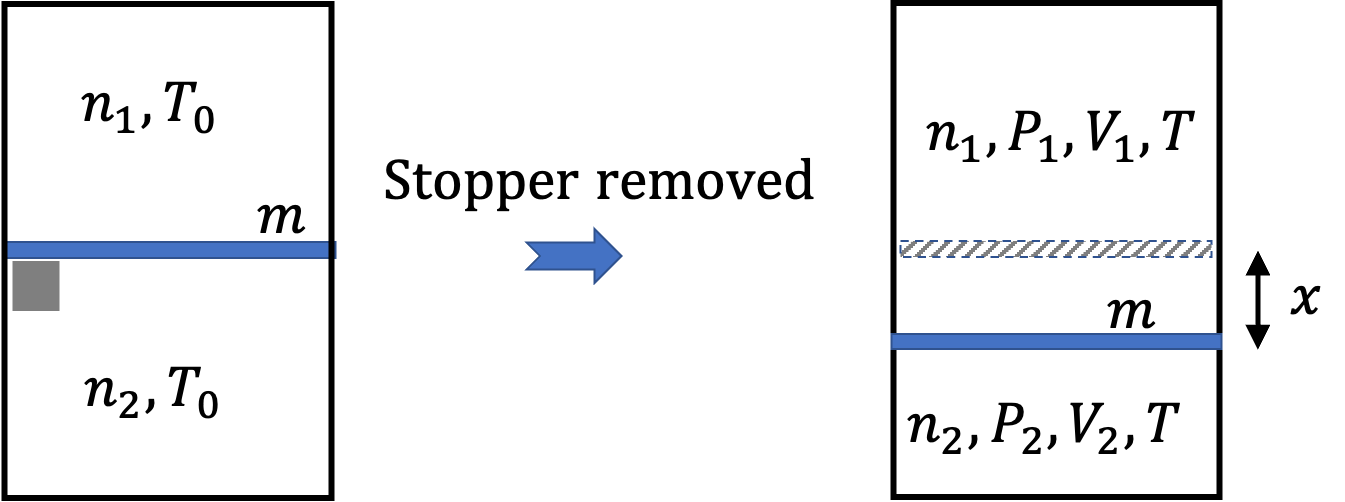
Since joint system of gas and piston is isolated from outside world, energy change in piston must be negative of energy change in gas. Let \(x\) be the drop in height of the piston as shown in Figure 2.2.10. Then, we must have
To find an expression of \(\Delta U_\text{gas}\text{,}\) we recall from memory that for an ideal gas, internal energy is given by
Since piston is diathermal, the two chambers will equilibrate to the same temperature. Denoting final temperature by \(T\) and initial temperature by \(T_0=300K\text{,}\) we find the expression for change in \(U\) as sum of changes in \(U\) of gas in the two chambers.
Putting this in Eq. (2.2.1) we get
Now, we look at the final system with two chambers and piston being in static equilibrium. Let \(P_1\) and \(P_2\) be pressures in the upper and lower chamber in the end.
Let \(A\) denote the area of cross-section of the piston. Balancing force on the piston in the final situation will give us another equation.
We can write this in terms of volume and temperature of the two chambers.
Since piston is diathermal, \(T_1=T_2=T\text{,}\) whose expression in \(x\) is given in Eq. (2.2.2). Since each side has same amount of gas \(n_1=n_2\) this equation can therefore, be rearranged to
In this equation \(T\text{,}\) \(V_1\) and \(V_2\) can be written in terms of \(x\text{,}\) which is the only unknown. Solving this equation should give us the final answer if we know \(C_V\text{.}\) Here \(C_V\) depends upon degrees of freedom for the molecules of the gas. Since no information about molecules is given, let us assume the simplest case and cosider it to be monatomic. In that case, we have only three translational degrees of freedom. this will give \(C_V = \frac{3}{2}R\text{.}\)
Multiply Eq. (2.2.3) by \(A\text{,}\) and write \(V_1 = (4+x)A\text{,}\) \(V_2=(4-x)A\text{,}\) and use \(T\) from Eq. (2.2.1) to get
Clearly dividing by \(n_1R\) will give us a simpler equation in \(a=mg/n_1R\text{.}\)
Numerically, we get
That means before we go forward with full numerical soluion, we divide out by 100, multily by 3, and use \(T_0=300\) to get
This will simplify to
Now, we need to solve
Hence,
Since \(x\) is positive in our case, answer will be \(x=1.78\text{.}\) Therefore, the distance from the top will be \(4+1.78 = 5.78 \approx 6\text{ m}\text{.}\)
Problem 2.2.11. Q7. Refraction at Spherical Interface.
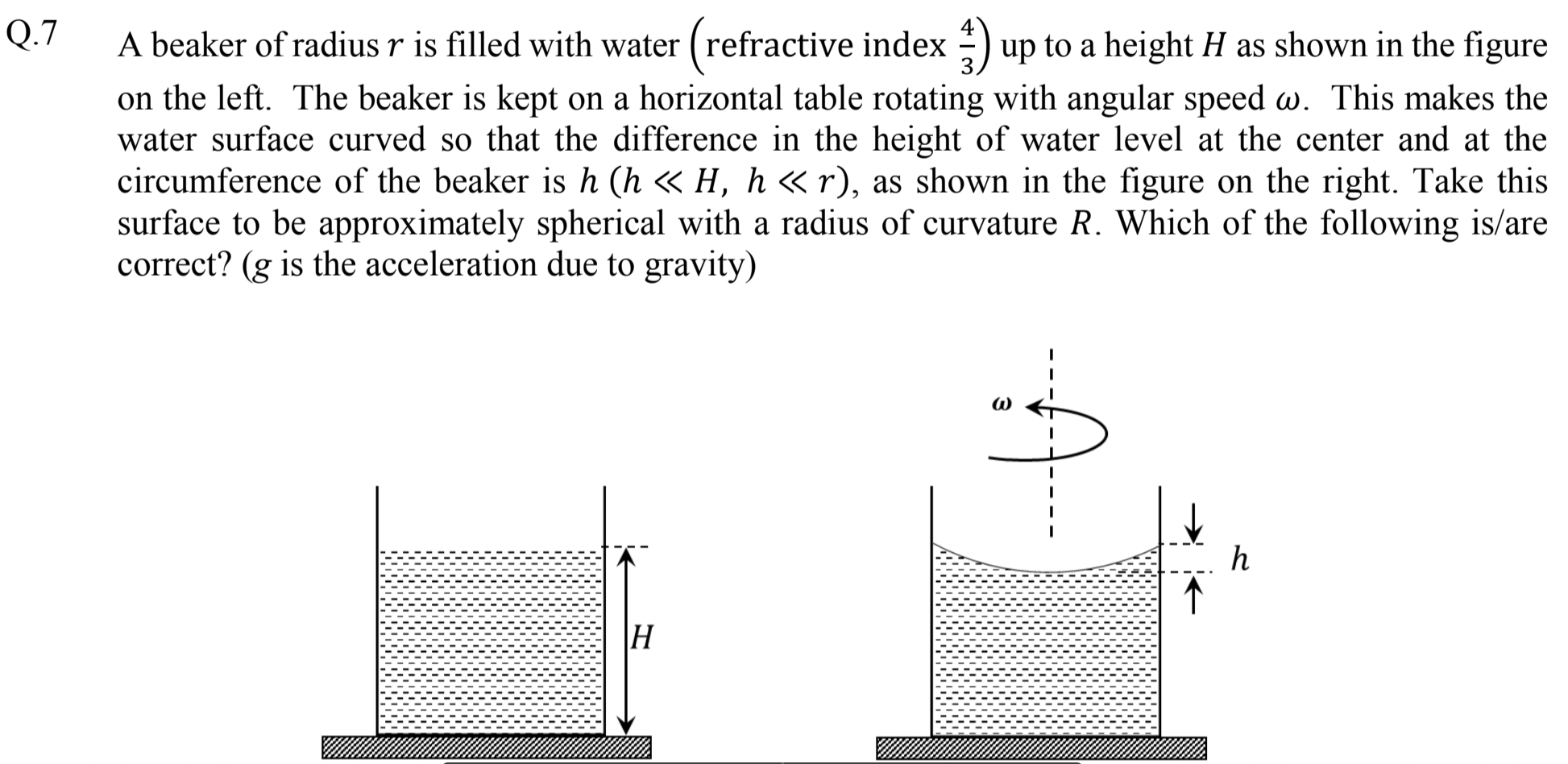

For (A) and (B), use geometry of a circle. For (C) and (D), you need formula \(h = \frac{\omega^2 r^2}{2g}\text{,}\) which you can deduce by balancing force on an element at the interface.
(A) and (D).
Parts (A) and (B) is about the geometry of the interface. Figure 2.2.12 shows relevant quantities. From the figure, we immediately get the following.
Therefore,

Hence,
Therefore, (A) is correct and (B) is incorrect.
From memory, I will just state the following result for the shape of the surface.
Therefore, radius of curvature of the interface in the limit \(h \ll r\) will be
The focal leength will be
Now, we use this in
With \(p=H\text{,}\) this gives
Hence,
This is (D). Clearly, (C) is incorrect. You could have guessed (C) is incorrect by just checking what you expect when \(\omega=0\) in this formula - you would expect \(3H/4\text{,}\) but you don't get that from (C).
Problem 2.2.13. Q8. Circular Motion.
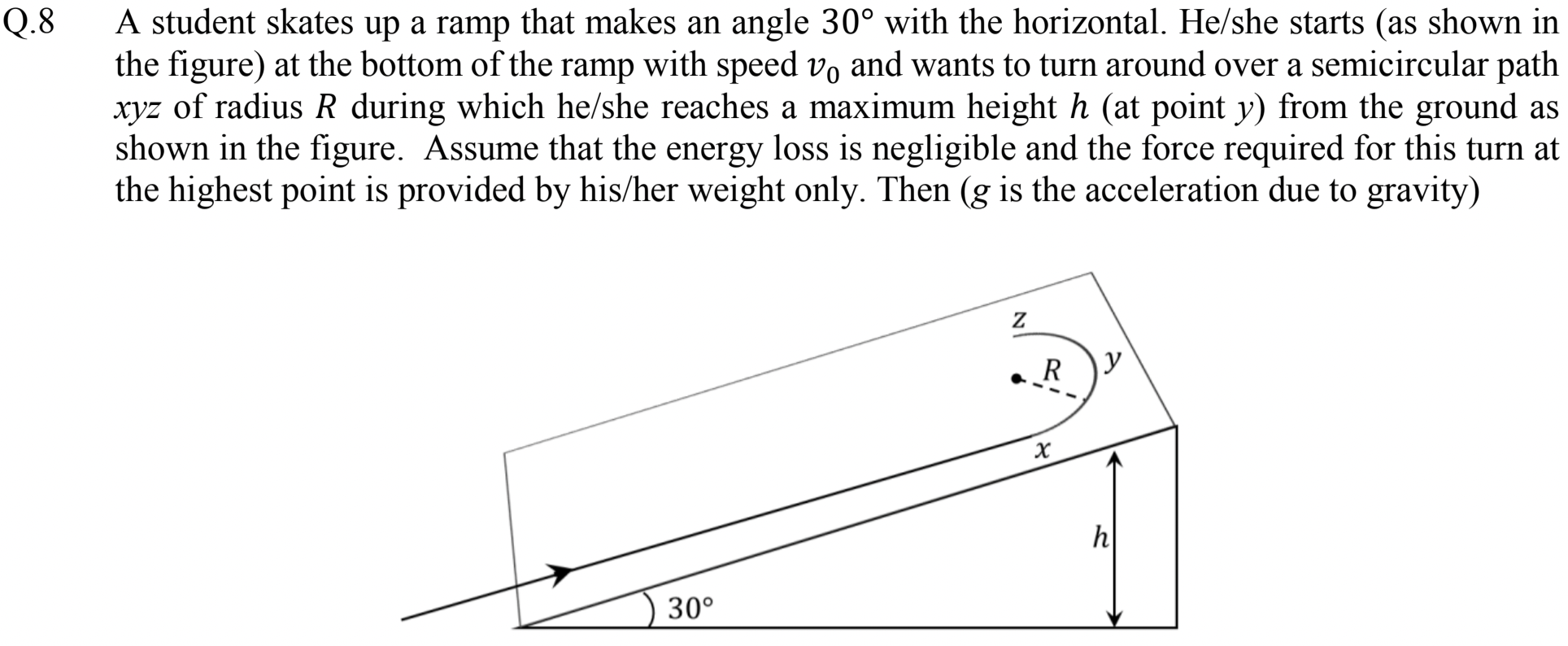

Use circular motion and conservation of energy.
(A) and (D)
By energy conservation speed \(v\) at the highest point \(y\) will obey
Therefore
Circular motion at \(y\) with circle in the plane of the board is possible by the component of weight \(mg\) along the board. This will give us
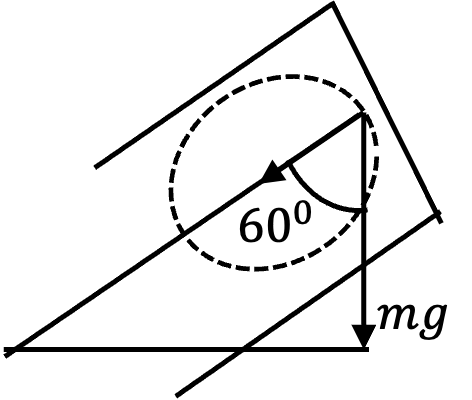
Hence,
Using this in Eq. (2.2.4) we get
That means (A) is correct and (B) is incorrect.
Supposing \(x\) and \(z\) are symmetric about \(y\) and lowest in the circular arc, I will present argument for \(x\) only. By using conservation of energy argument we note the following.
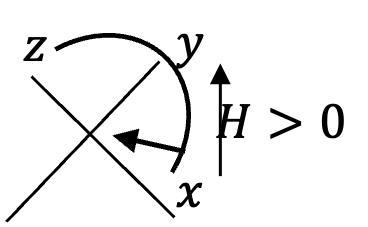
Since \(H>0\text{,}\) \(v_x>v_y\text{.}\) Since \(x\) and \(z\) are lowest in the arc, speed there must be highest. Hence, centripetal forces, which equal \(m v_x^2/R\) and \(m v_z^2/R\text{,}\) will be the highest. Therefore, (D) is correct and (C) is incorrect.
Problem 2.2.16. Q9. Ballistic Pendulum.
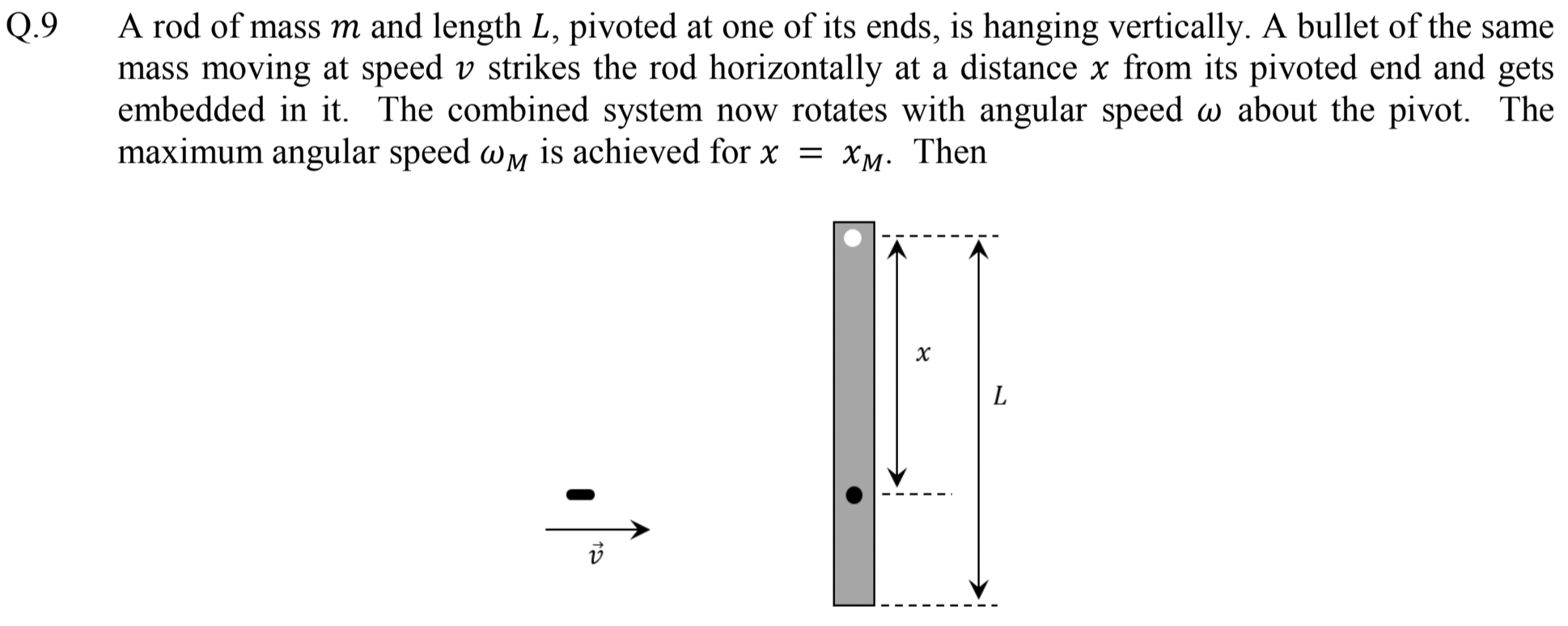

For A and B use angular momentum conservation. for (C) and (D) use \(d\omega/dx=0\text{.}\)
(A), (C), (D).
The impact will conserve angular momentum. Angular momentum before impact will be angular momentum of the bullet about point O, given by \(L_i = mvx\) in direction coming out of page. Let \(\omega\) be angular velocity after the impact. At that point angular momentum will be sum of angular momentum of the bullet and that of the rod.
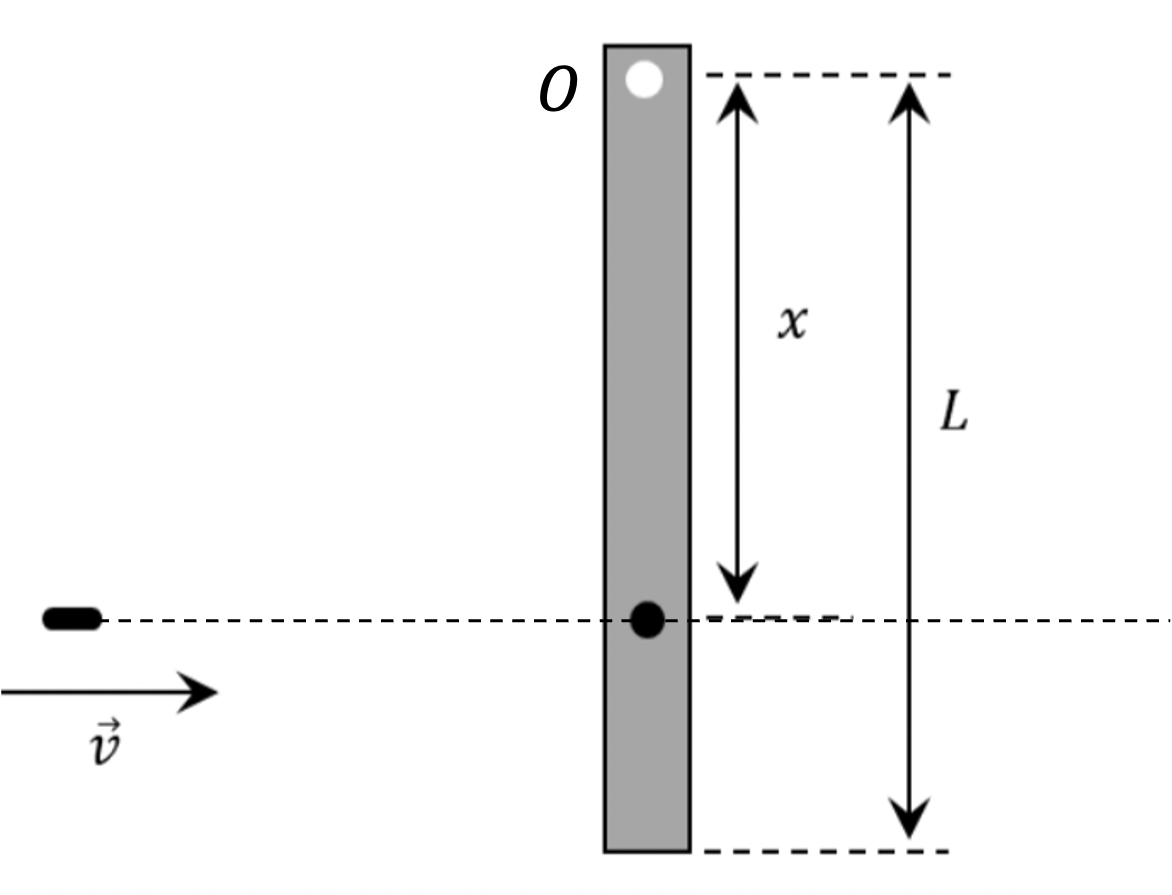
By conservation of angular momentum, we get
Therefore,
That is (A) is correct and (B) is incorrect.
We want \(x\) for which \(\omega\) will be maximum. That is, we treat \(\omega(x)\) as a function of \(x\) and set first derivative to zero.
We rewrite \(\omega\) formula we obtained in Eq. (2.2.6) as
Now, take derivative with respect to \(x\text{.}\)
Now, \(d\omega/dt=0\) will mean
Hence,
This gives \(x_M = L/\sqrt{3}\text{,}\) which is (C).
Now, we use this in Eq. (2.2.6) to get
This is (D).
Problem 2.2.18. Q10. X-ray Tube.

Figure 2.2.19 shows schematics of an X-ray tube. 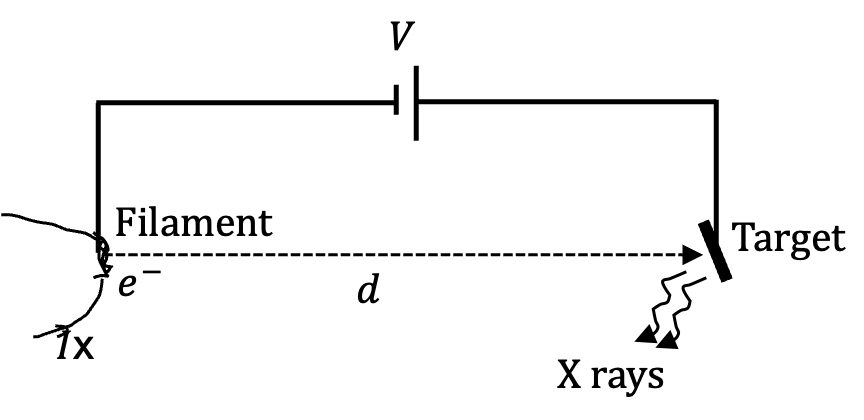
Reducing the curent \(I\) does not affect the kinetic energy of electron striking the target - reducing filament current reduces the number of electrons that get emitted. But, increasing the voltage between filament and target increases the kinetic energy.
When we double the voltage between target and filament, we will double the kinetic energy of electrons reaching the target. The largest frequency will become double, or equivalently, the smallest wavelength emitted will then become half as much.
When filament current \(I\) is reduced \(\frac{1}{2}I\text{,}\) that will mean less power output. That will mean less number of electrons striking the target. That means less X-ray photons emitted. That means intensity of all X-rays go down.
Neither KE or number of striking electrons have any effect on wavelengths of the characteristic, which is a charaxterisitic of the target.
Comclusion: (A) and (C) are correct.
Problem 2.2.20. Q11. Dielectric Screening.

Use dielectric shielding and balance forces in the two situations.
(B), (C).
We have two situations for the changes as shown in Figure 2.2.21.
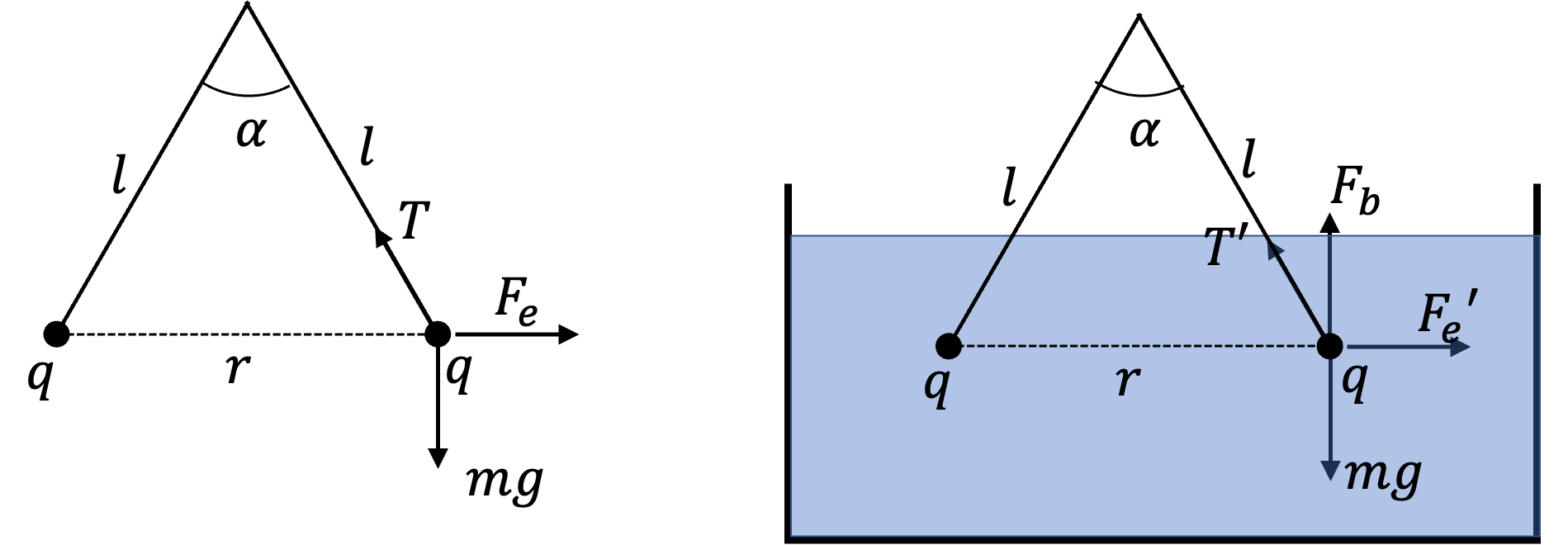
For the sake of brevity in writing, let us introduce symbol for half angle.
Now, balancing forces on one of the charges when they are in air (figure on the left) gives
When charges are in a dielectric, electric force will be divided by the dielectric constant \(K\text{.}\)
Now, we also have the buoyancy force,
where \(V\) is the volume of the charge,
where \(m\) is mass of the charge and \(\rho_0\) its density. Balancing forces when the charges are immersed in the dielectric gives us
First we isolate \(T'\, \cos\beta\) in Eq. (2.2.10),
and take ratio with Eq. (2.2.8) to get
Now, we can take a ratio of Eq. (2.2.7) and (2.2.9) and use the ratio of tensions to get
The left side here is just dielectric constant \(K\text{.}\) thus,
This gives
Hence,
Let's summarize the choices. (A) is incorrect, (B) is correct, (C) is correct, (D) is incorrect. You could have got (B) even without working out anything since that is obvious from electric field shielding by a dielectric.
Problem 2.2.22. Q12. Kinematics.

Use derivatives with respect to time to get veocity and acceleration components.
(A), (B), (C), (D).
This is purely algebra problem. By taking time derivatibves of the trajectory, \(y = \frac{x^2}{2}\text{,}\) we get the following relations between components of velocity and acceleration.
Now, we check the choices.
(A) At \(x=y=0\text{,}\) \(v_y=0\text{.}\) That means give speed at origin is all \(v_x\text{.}\) That is \(v_x=1\text{ m/s}\text{.}\) Hence, acceleration will be
Therefore, (A) is OK, although not for the reason given in (A).
(B) If \(a_x=0\text{,}\) we will get
Since \(a_x=0\text{,}\) \(v_x\) does not change, which was set to \(1\text{ m/s}\) at \(t=0\text{.}\) Hence,
Therefore, B is OK.
(C) This is obviously correct based on what we did in (A).
For (D), we will note that when \(a_x=0\text{,}\) we had \(a_y=1\text{ m/s}^2\text{.}\) Therefore at \(1\text sec\text{,}\) \(v_y=1\text{ m/s}\text{.}\) We already know unchanging \(v_x = 1\text{ m/s}\text{.}\) Since \(v_x\) and \(v_y\) are equal, velocity is pointed at \(45^\circ\text{.}\) Therfore (D) is also OK.
This was a totally stupid problem.
Problem 2.2.23. Q13. Adiabatic Work.
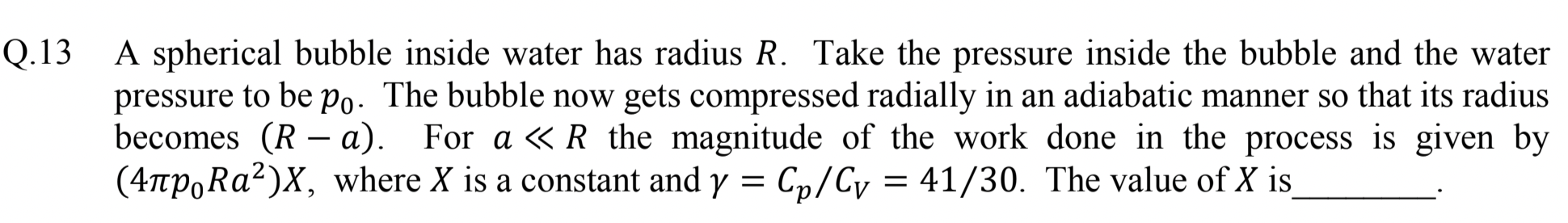
Use \(pV^\gamma=\text{constant}\) for adiabatic process. Use McLaurin expnasion of \((1+x)^a\) up to second order.
\(2.05\text{.}\)
Figure 2.2.24 shows the problem in a diagram. Initially, gas inside the bubble is at presure \(p_0\) and volume \(V=\frac{4}{3}\pi R^3\text{.}\) Bubble is compressed adiabatically to pressure \(p_f\text{,}\) which is a sum of pressure from water \(p_0\) and an external agent \(p_\text{ext}\text{.}\) Figure shows an infinitesimal part of the process when the bubble's radius is compressed from \(r\) to \(r-dr\text{.}\)
Question asks us to find an expression for \(W_\text{ext}\) by the external agent in the case that \(a \ll R\text{.}\) Since gas is being compressed adiabatically, we have the following equality.
where \(p_i=p_0\text{,}\) \(V_i=\frac{4}{3}\pi R^3\text{,}\) \((p,\ V)\) are pressure and volume inside the bubble at arbitrary point, and \(\gamma=Cp/C_V\text{,}\) whose value for the gas at hand is given in the problem. In particular, when we reach the final volume at radius of the bubble, \(R-a\text{,}\) we have
Now, notice that since \(p_\text{gas} = p_\text{ext} + p_0\text{,}\) we can write work by external agent for infintesimal volume change \(dV\) will be
where I have placed minus sign since \(dV \lt 0\) and we want \(W_\text{ext}\) positive. Now, using Eq. (2.2.12) for \(p_\text{gas}=p\text{,}\) we transform this to
We integrate this from \(V=V_i\) to \(V=V_f\) to get
Now, we expand \(V_f/V_i\) and its powers in powers of small parameter \(a/R\text{.}\) We will keep up to \((a/R)^2\) since the final answer in the problem is of this order. Probably the constant and \(a/R\) terms cancel out. We will see that. To help with expansion we recall Binomial expansion.
We just need three terms in this expansion. Let's use \(x=a/R\) in our formulas. Hence,
Similarly
Now, using these approximate expressions in Eq. (2.2.14), we get
Equating this to the expression given in the problem statement, we get
Problem 2.2.25. Q14. Bridge Circuit.
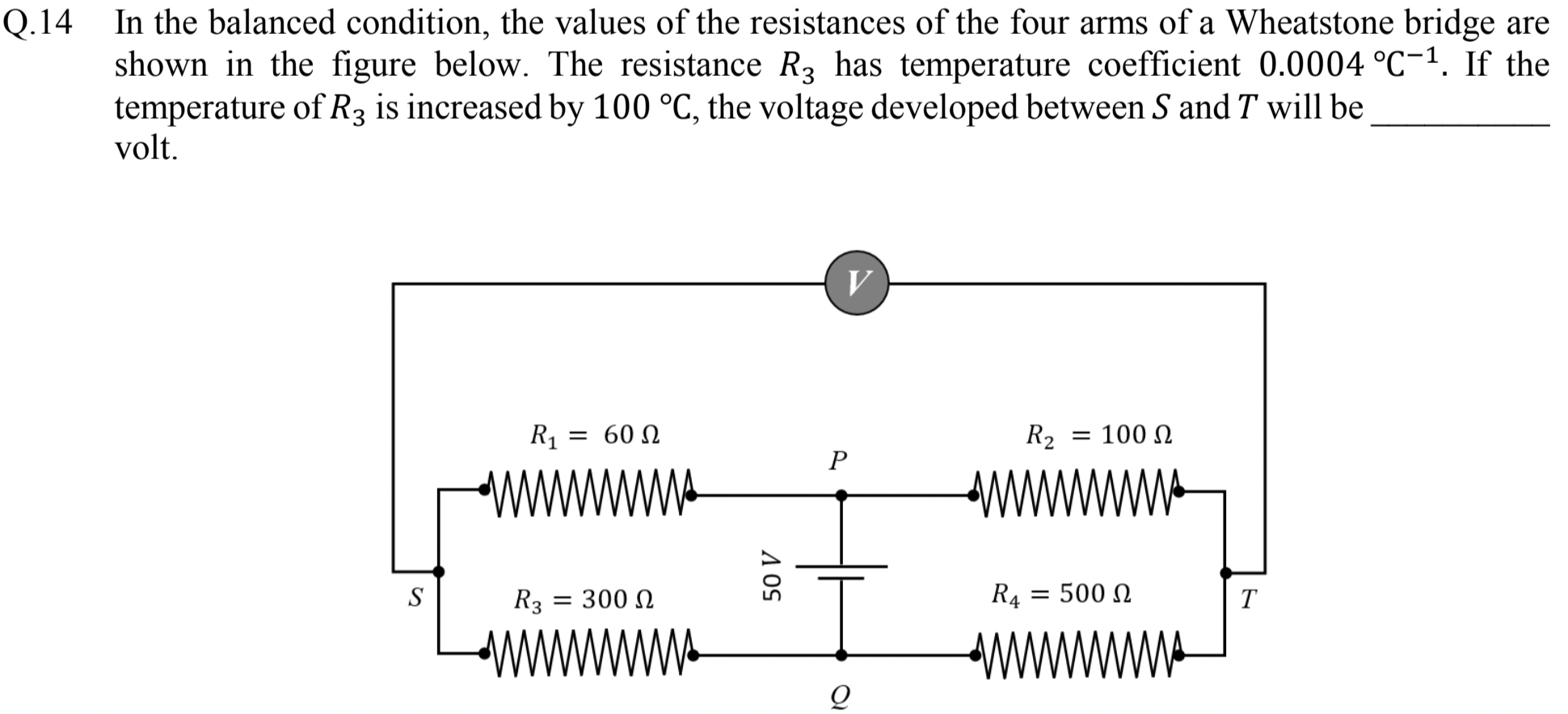
Negligible current flows through the voltmeter.
\(0.27\text{ V}\text{.}\)
Let's label the circuit with currents and voltage at P and Q as shown in Figure 2.2.26. The resistance \(R'_3\) is
Since very small amount of current flows through a voltmeter, same current \(I_1\) flows through both \(R_1\) and \(R'_3\) and same current \(I_2\) flows through both \(R_2\) and \(R_4\text{.}\)
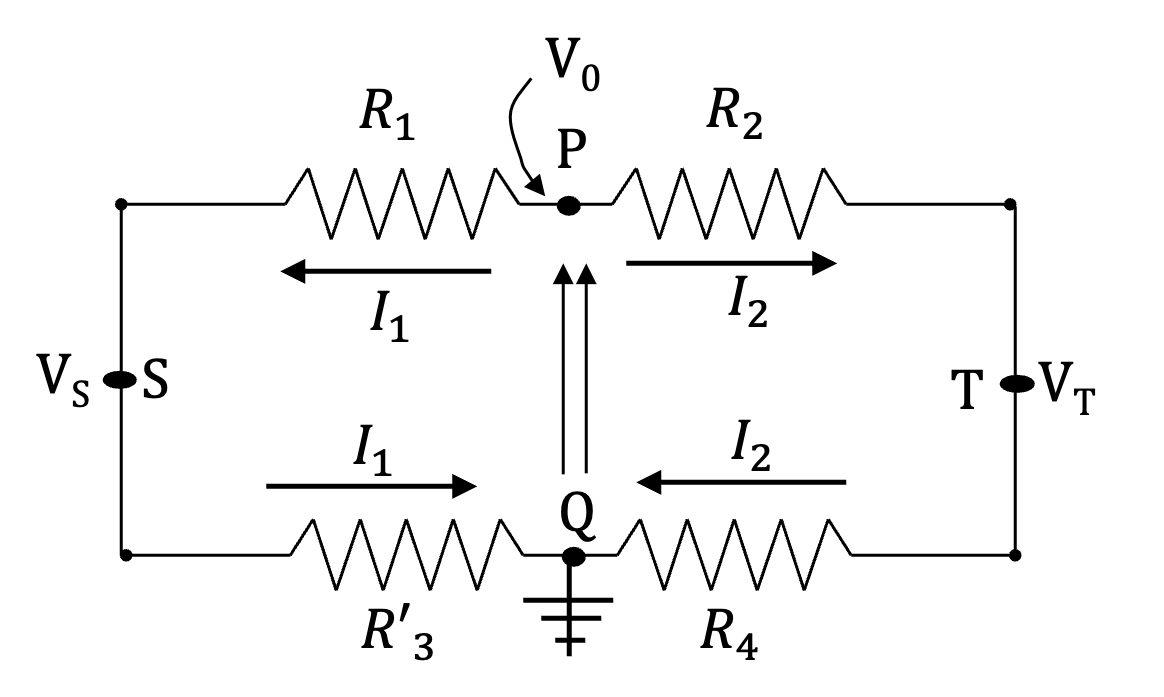
Let \(V_S\) and \(V_T\) denote voltages at S and T. Voltage drops \(R_1\) and \(R'_3\) gives
Therefore,
Similarly, we get the following from the other end of the circuit.
Therefore,
Hence,
Problem 2.2.27. Q15. Relative Error.
For product \(f = x^ay^b\text{,}\) its better to work with \(\Delta f / f\text{.}\)
\(1.3\%\text{.}\)
Equivalent capacitance of the two capacitors in series is
Net energy stored in the two capacitors will be
Thinking of \(U\) as a function of \(C_\text{eq}\) and \(V\text{,}\) we obtain
Since \(U\) is a product, its best to divide this by \(U\text{.}\)
For \(\Delta C_\text{eq}\) we work with inverse of \(C_\text{eq}\text{.}\)
Therefore,
Hence,
Now, we have all the pieces for numerical work.
Hence, from Eq. (2.2.16), we will get
That is \(1.3\%\text{.}\) I believe this is the answer expected in the exam. But, this is not how you would obtain error in experiment. You normally add independent errors in quadrature, i.e.,
This formula will give
This will be \(0.94\%\text{,}\) not \(1.3\%\text{.}\)
Problem 2.2.28. Q16. Hooke's Law.
Use Hooke's law in the form, \(dp/dV = - B V\text{.}\)
\(0.24\text{ mm}\text{.}\)
We use Hooke's law in the form
With \(V=L^3\text{,}\) this becomes
Integrating we get
In the last step I used \(\Delta L \ll L_i\) and kept only the leading term in the expansion for natural log. Hence,
Problem 2.2.29. Q17. Induced EMF.
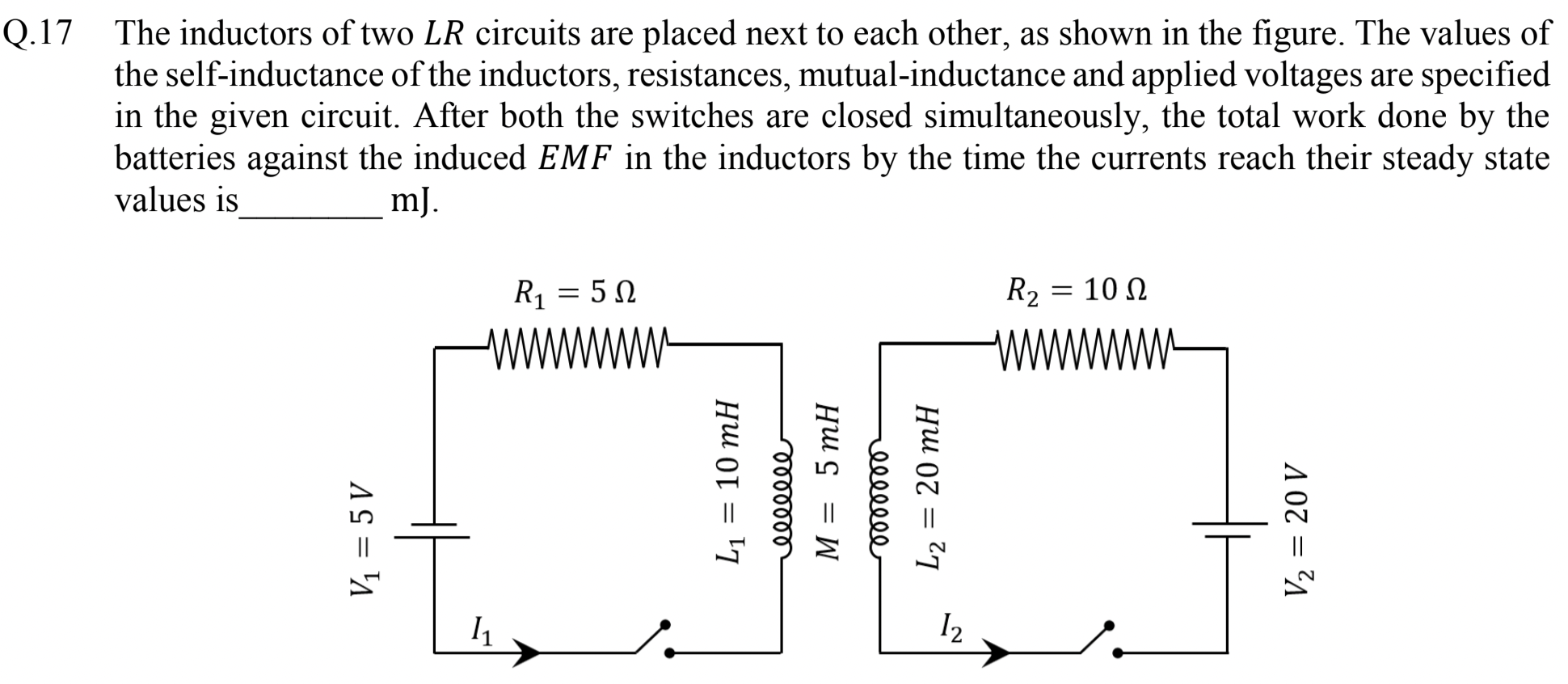
Just look at induced EMF in the two circuits.
\(55\text{ mJ}\text{.}\)
Since we need work against the induced EMF, let us find expression for induced EMF in the two circuits. The will obey the following equations of motion.
Therefore, work against these EMFs in time \(dt\) will be
The total will be
Integrating we get
Problem 2.2.30. Q18. Detailed Balance.

At steady state, the rate on increase in temeperature will be rate of decrease of temperature.
\(8.33\,^\circ \text{C}\text{.}\)
The rate of energy deposit by sun, as heat, will be
Using definition of specific heat, we know that for mass \(m\) energy \(dQ\) will increase temperature by \(d T\) as given by
Hence, we get rate of increase of temperature as
By Newton's law of cooling rate of decrease in temeperature will be
Equating these two rates for steady state we get
