Section 3.1 Paper I
Problem 3.1.1. Q1. Graviation in a Spherical Mass Distribution.

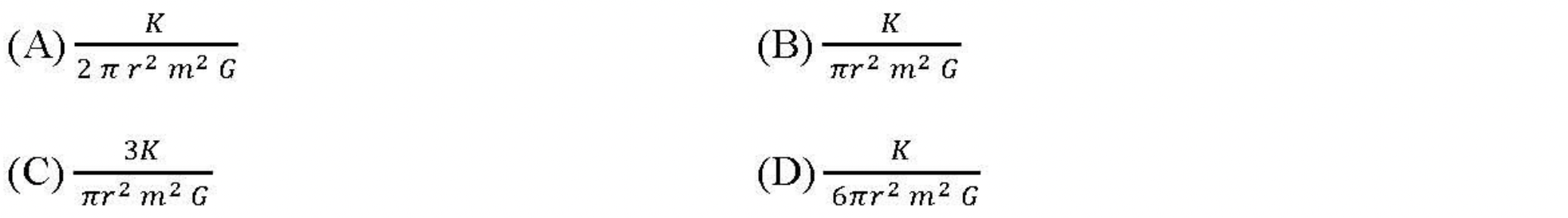
Force from mass enclosed only.
(A).
Figure 3.1.2 shows the situation for a particle of mass \(m\) moving at radius \(r\) of the spherical mass distribution. The force on \(m\) will be mass \(M_r\) that is inside the sphere of radius \(r\)
Since \(\rho(r)\) is density that varies inside the sphere we will get Mass \(M_r\) will be
The radially inward \(\vec F = m \vec a\) with \(a = v^2/r\) gives
Using kinetic energy \(K = \frac{1}{2}m v^2\text{,}\) this becomes
We now take derivative of both sides of this equation with respect to \(r\text{.}\)
Now, from Eq. (3.1.1) we have \(dM_r/dr\) \(= \rho(r) 4\pi {r}^2\text{.}\) Therefore, we get
Since \(\rho(r) = n(r) m \text{,}\) where \(n(r)\) is the number density, we get
This is choice (A).
Problem 3.1.3. Q2. Static Electricity of Charge Distribution with a Hole.


Think of a hole as two point charges \(\pm dq\text{.}\)
(C)
It looks like we have four problems (A), (B), (C), and (D). Only one of them is right. We will work in order and if we find correct one, we will stop.
First let \(Q\) be the charge on the spherical shell without the hole. Since we have spherical symmetry, we can pretend all the charges at the center and potential of such a point charge at a distance \(R\) will give us the amount of charge on the shell. Thus,
That is
Second thing to notice is the potential and field of a charged shell with a tiny hole to be equal to the superposition of these quentities of (1) charged shell without the hole and (2) a point charge of the opposite sign at the point of the hole.
Since \(Q\) is distributed over the area \(A=4\pi R^2\) and hole has area \(a=\alpha 4\pi R^2\text{,}\) the point charge we need in Figure 3.1.4 is negative of \(Q\) and equal to
Now, let us check the choices.
(A):
Change in potential will be equal to the potential by \(q\) at a distance \(R\) from P.
Comparing this to the given answer shows that (A) is incorrect.
(B):
Originally, we had zero electric field at the center. Now, we will have electric field of \(q\text{.}\) Its magnitude will be
Comparing this to the given answer shows that (B) is incorrect.
(C):
Originally, we had electric potential at the center to be \(V_0\text{.}\) With the drop in potential found when we worked out (A) above, we have
The potential at midway to the center will be a sum of the original and the change due to \(q\text{.}\) Change will be the potential due to \(q\text{.}\)
Therefore,
Their ratio turns out to be
Comparing this to the given answer shows that (C) is correct. Since, we found the correct choice in a single correct choice question, we don't need to look at (D), which should be incorrect. But, just in case, I will check that also.
(D):
Potential at a point outside the shpherical shell will be given by the potential of a point charge of value \(Q\) pretended to be at the center.
To this we need to add the potential of \(q\text{,}\) which is
Thus, answer should be
which is not what is given in (D), which makes (D) incorrect choice.
Problem 3.1.5. Q3. Heating a Metal.

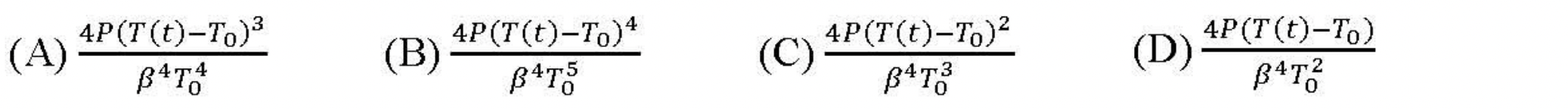
Use \(m C dT/dt = P_\text{in}\text{.}\)
(A).
All the energy entering the metal in time \(dt\) goes towards raising its temperature by \(dT\text{.}\) Let \(C\) be the specific heat of the metal and \(m\) be its mass. Then, we have
We have been given \(T(t) = T_0\left( 1 + \beta t^{1/4}\right)\text{.}\) Using that
Therefore, heat capacity, which is \(mC\) will be
We need to replace \(t\) in this in fravor of \(T\) using the given formula for \(T\text{.}\)
Hence,
This is (A).
Problem 3.1.6. Q4. A Two-mode Nuclear Decay.

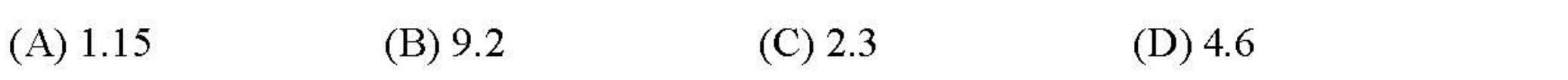
Decay constants will add: \(\lambda = \lambda_1 + \lambda_2\text{.}\)
(B)
There are two modes of decay as shown in Figure 3.1.7. In such scenario, effective decay constant is sum of the decay constants of all the modes. Thus, number of \(^{40}_{19}\text{K}\) left after time \(t\text{,}\) \(N_t\) will be
The number of potassium that have decayed will be
which will be the sum of Ca and Ar atoms in the sample. Thus, from the given data we have
Using this in the formula for \(N_t\) given above, we get
Taking natural log of both sides we get
Stripping away the factor \(10^9\) we get \(9.2\text{,}\) which is choice (B).
Problem 3.1.8. Q5. Capillary Action in a Tube with Varying Contact Angles.

Use of \(2\gamma\cos\theta/ \rho g r\) for a single tube.
(A), (B), (C)
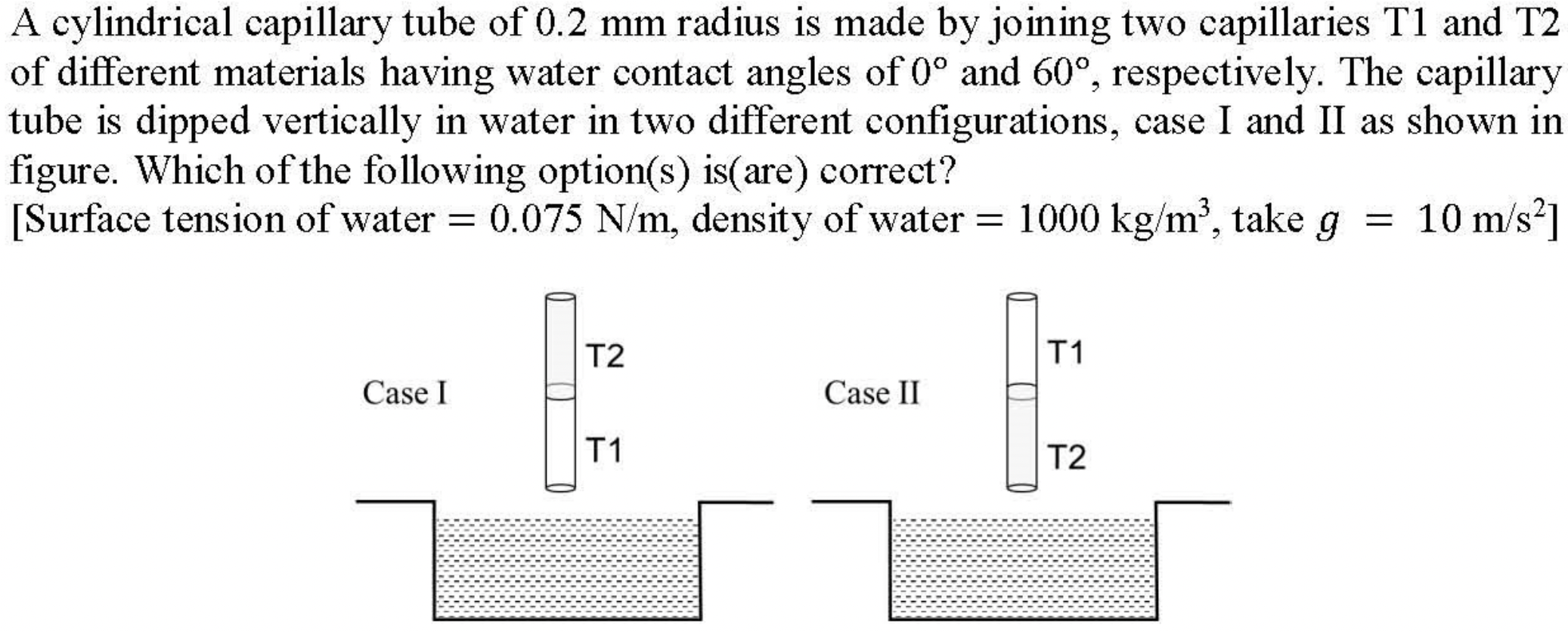
(A): As Figure 3.1.9 shows the meniscus of tube \(T_2\) will contribute more to the weight balanced by the surface tension. Hence, the correction to the height formula will be different. That is, (A) is correct.
(B) & (C): As Figure 3.1.10 shows balancing weight of the liquid in the tube by the surface tension gives
where \(\gamma\) is the surface tension.
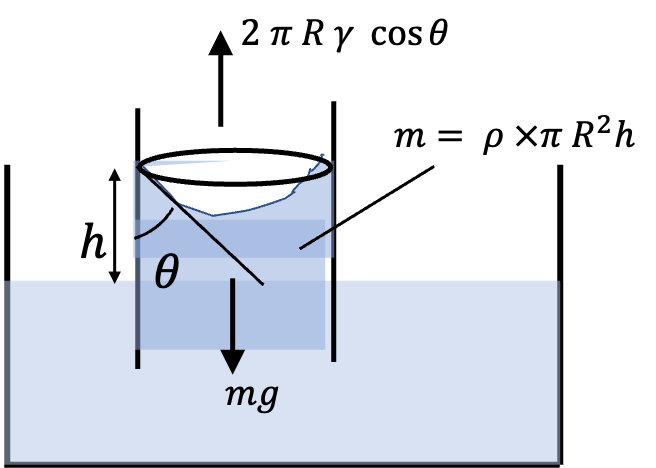
This simplifies to
For given values of constants we get \(h\) in meters to be
For (B), with \(\theta = 60^\circ\text{,}\) we get
That means (B) is correct.
For (C), with \(\theta = 0\text{,}\) we get
That means (C) is also correct.
For (D), since available height is only \(5\text{ cm}\) while in tube of type \(T_1\text{,}\) we expect to rise to height \(7.5\text{ cm}\) before it encounters a tube of contact angle that is larger. The liquid will stop at height of \(5\text{ cm}\) as we can easily show.
Let the liquid rises by a height \(y\) in tube \(T_1\) abive the \(5\text{ cm}\text{.}\) The surface tension will correspond to \(\theta=0\) since it is the tube at the top. The surface tension must support a height of \(5\text{ cm} + y\) with \(y \ge 0\text{.}\) Thus, we require
Solve for \(y\) to get
That is not possible. Hence choice (D) will be incorrect.
Problem 3.1.11. Q6. Induced EMF in a Wire Moving in a Magnetic Field.
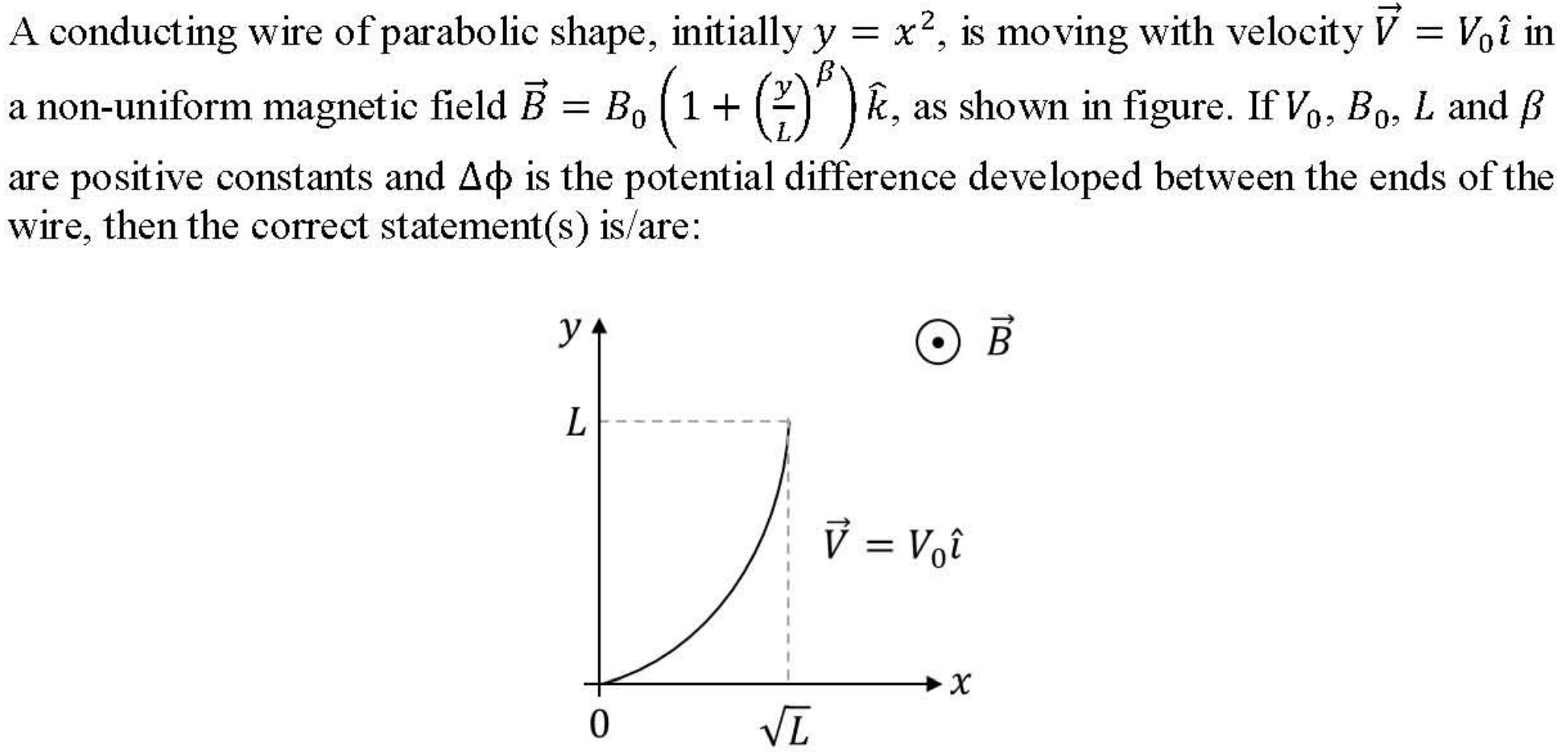

Think of flux through a strip of width \(dy\text{.}\)
(B), (C), (D).
This is clearly a Faraday's law problem. We want rate of flux change. For that we need to compute change in flux between instant \(t\) and \(t+\Delta t\text{.}\) Since \(B\) is a function only of \(y\text{,}\) we pick a strip between \(y\) and \(y+\Delta y\) as shown in Figure 3.1.12.
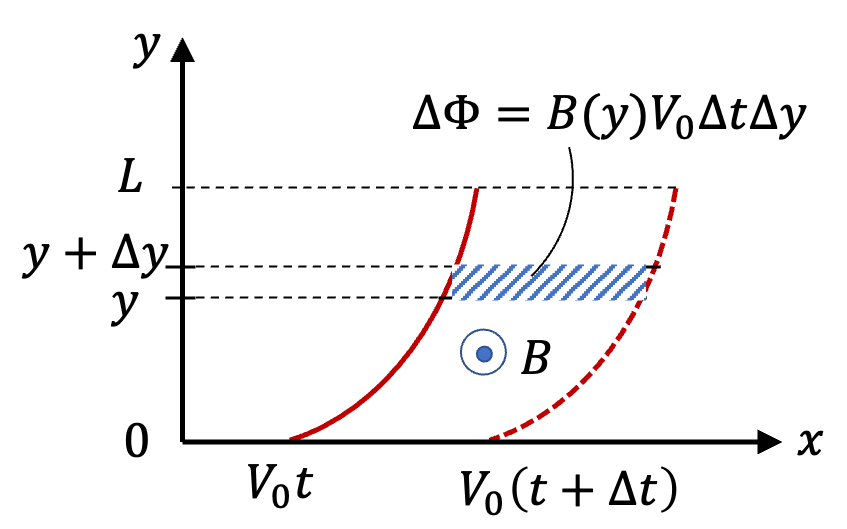
Therefore, induced EMF due to flux through the strip will be (dropping the absolute sign for the moment)
Infinitesimal strip will give
By integrating this we will get the net EMF induced in the moving wire.
(A): To check (A), we set \(\beta = 0\) in Eq. (3.1.3). This gives induced EMF to be \(2B_0V_0L\text{,}\) which means choice (A) is incorrect.
(B): To check (B), we set \(\beta = 2\) in Eq. (3.1.3). This gives induced EMF to be \(\dfrac{4}{3}B_0V_0L\text{,}\) which means choice (B) is correct.
(C): (C) is obviously correct since we only needed the limits on \(y\) values, which does not depend on the shape of the wire.
(D): (D) is obviously correct from Eq. (3.1.3) where we see \(\mathcal{E} \propto L\text{.}\)
Problem 3.1.13. Q7. RC Circuit with Two Switches.


Uncharged capacitor is like a short in the circuit. Fully charged capacitor is like open circuit.
(A), (B), (D)
(A) & (B): Since switch \(S_2\) is open for these parts, that branch is not in the circuit. Figure 3.1.14 shows the simplified circuit for this part. All circuit elements are in series and they can be simplified to obtain equivalent quantities.
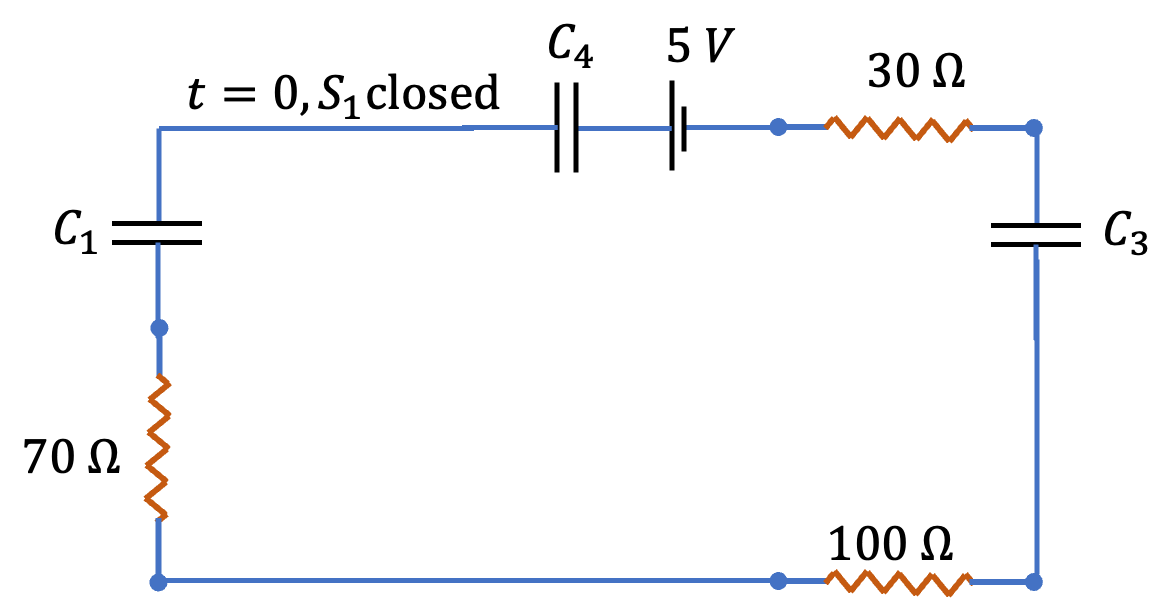
Equivalent resistance is
Inverse of equivalent capacitance is
Therefore,
(A) is asking for current just when switch \(S_1\) was closed. At that time, no charge was built on capacitors. So, capacitors are like shorts. There is only voltage source, net voltage across the equivalent resitance is the voltage of that source.
That is \(25\text{ mA}\text{.}\) Hence choice (A) is correct.
(B) is asking for voltage across capacitor \(C_1\) when all capacitors are fully charged. At that point there will ne no current and hence no drop in voltage across the resistors. Using equivalent capacitance in capacitor formula we can find the charges on the equivalent capacitor. But since capacitors are all in series, they will all have the same charge.
This is also on capacitor \(C_1\text{.}\)
Now using capcitor formula on this capacitor we get
Therefore choice (B) is correct.
(C) & (D): Since switch \(S_1\) was open for a long time, capacitors \(C_1\text{,}\) \(C_3\) and \(C_4\) are charged at the instant \(S_2\) is closed. We mark this instant to be new \(t=0\) as shown in Figure 3.1.15.
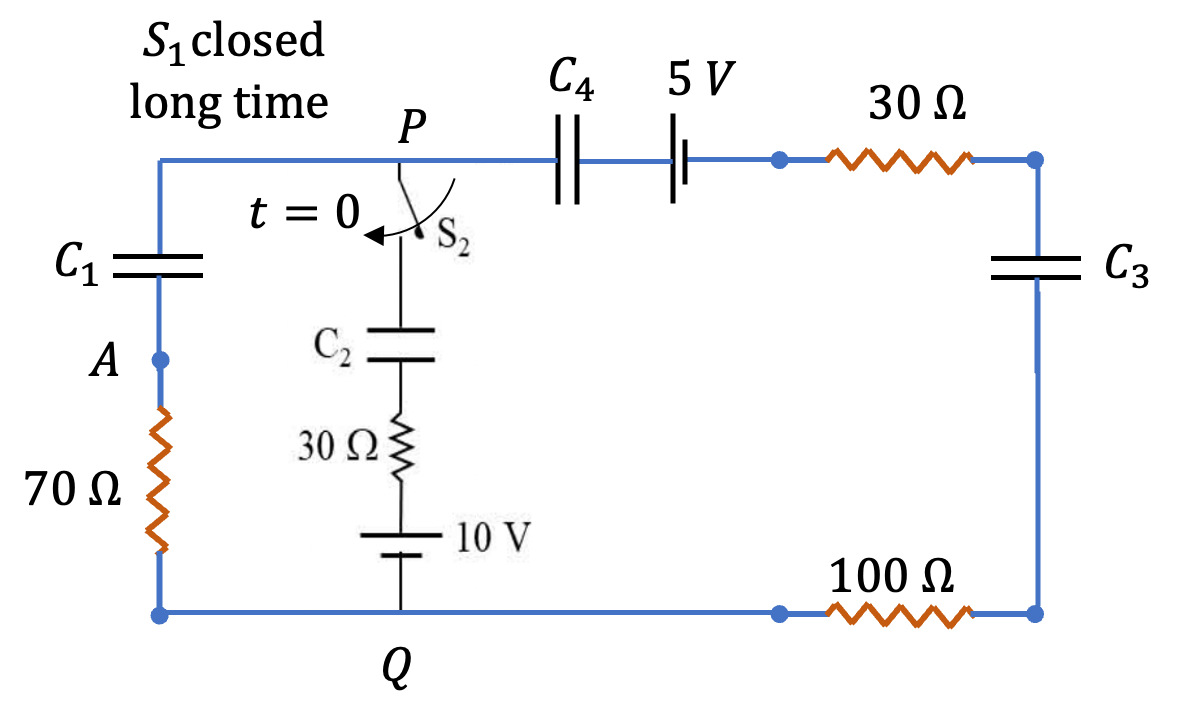
(D): An instant before \(t=0\text{,}\) no voltage drops across the \(70\;\Omega\) resistor. Therefore, voltage across P and Q is
That makes (D) in correct.
(C): This is after switch \(S_2\) is closed when capacitors \(C_1\text{,}\) \(C_3\) and \(C_4\) are fully charged and capacitor \(C_2\) is uncharged. That will mean capacitors \(C_1\text{,}\) \(C_3\) and \(C_4\) will be voltage sources and capacitor \(C_2\) will be just a short. The circuit with labels is shown in Figure 3.1.16.
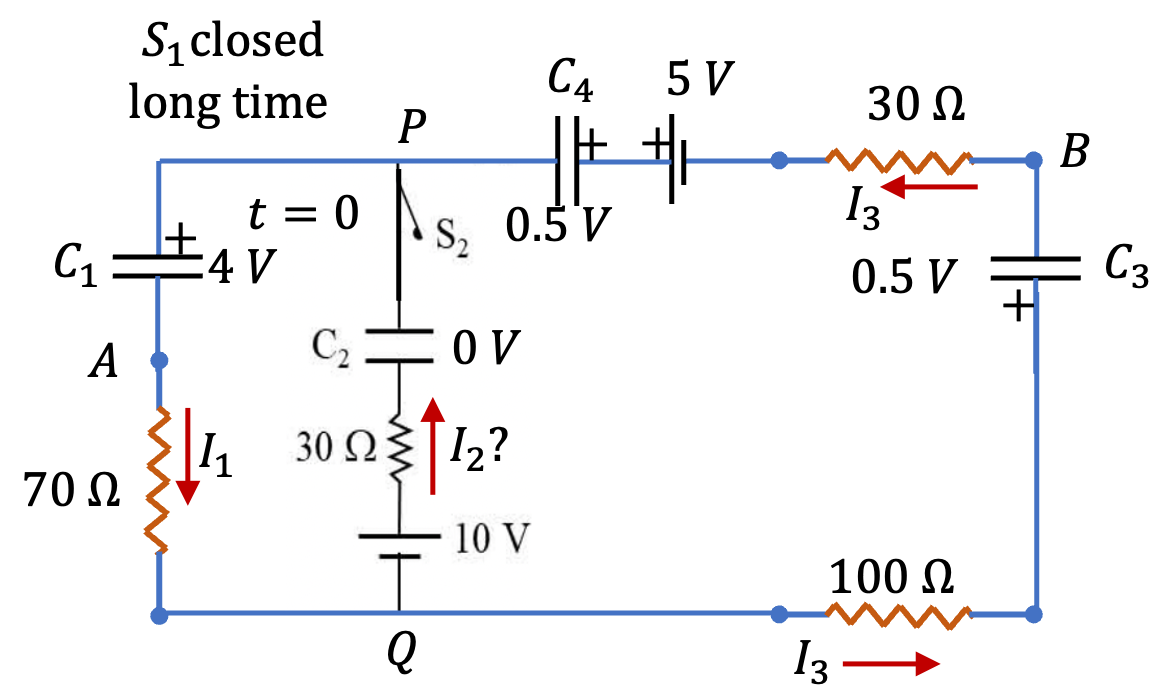
To find \(I_2\text{,}\) we will use Kirchoof's rules.
Simplifying Eq. (3.1.6) and using \(I_3\) from there into Eq. (3.1.4) we get
Use this in Eq. (3.1.5) to get
This gives
This shows that given answer of \(0.2\text{ A}\) is not correct. Incidently, if you ignore any current in the outer loop as was the case when only switch \(S_1\) was closed, you would get \(0.2\text{ A}\text{,}\) but that isn not the situation at an instant after \(S_2\) is closed.
Problem 3.1.17. Q8. Gauss's Law.

For (C) and (D) you will need to figure out surface area of a spherical cap.
(A), (B), (C)
Think of the surface of the cylinder in these problems as Gaussian surface and use Gauss's law for them. Recall that Gauss's law states that electric flux through a closed surface \(S\) will be
(A): Since entire charged spherical shell is within the space enclosed by the surface of this cylinder, \(Q_\text{enclosed} = Q\text{.}\) Hence, flux through this surface will be \(\Phi = Q/\epsilon_0\text{,}\) which is the given answer. So, (A) is correct.
(B): Since entire charged spherical shell is outside the space enclosed by the surface of this cylinder, \(Q_\text{enclosed} = 0\text{.}\) Hence flux through this surface will be \(\Phi = 0\text{,}\) which is the given answer. So, (B) is correct.
This cylinderical surface cuts through the charged shell. The enclosed charges are on spherical caps on the two ends.
(C): The cylinder now cuts through the sphere as shown in Figure 3.1.18. The enclosed charges are now on the two spherical caps shown. Area of each cap is
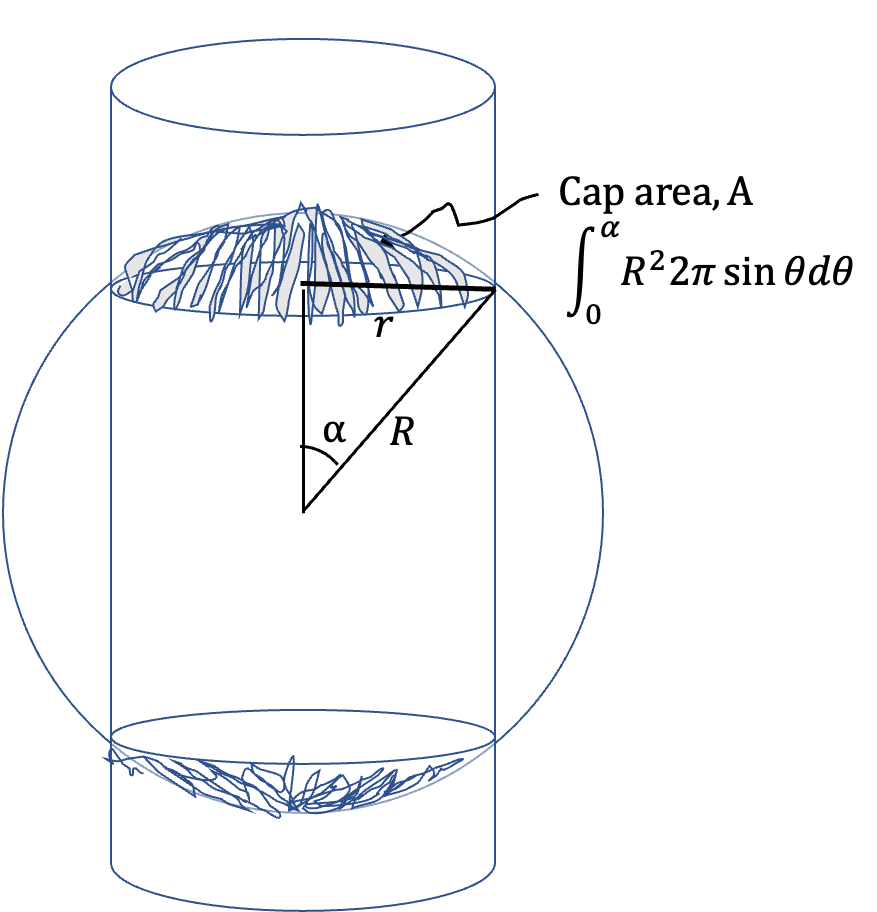
Therefore, total area of interest is twice this much. Since \(Q\) is evenly spread out over \(4\pi R^2\text{,}\) enclosed charges are
With \(\cos\alpha = \sqrt{R^2 - r^2}/R = \sqrt( 1 - (r/R)^2)\text{,}\) this will be
For (C), we have \(r = 3R/5\text{,}\) therefore,
This says that choice (C) is correct.
For (D), we have \(r = 4 R/5\text{,}\) therefore,
This says that choice (D) is incorrect.
Problem 3.1.19. Q9. Ideal Gas Cyclic Process in TV Plane.
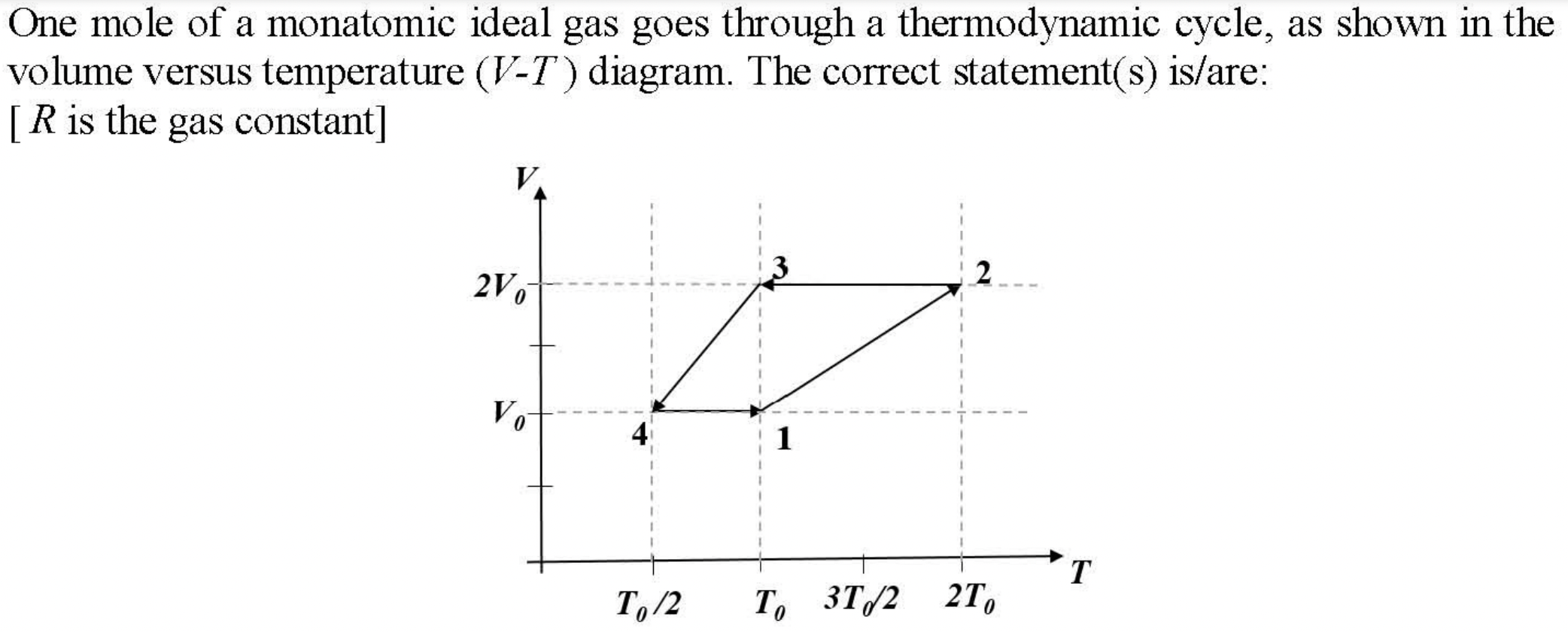

In an ideal gas \(V = a T\) means \(P\) must be constant.
(A), (C).
(A): Work around the cycle will be sum of work for each process. We need a formula for work in \((T, V)\) plane for an ideal gas. We get that from \(pdV\text{.}\)
where I have kept \(T\) inside the integral since we will have \(T\) vary as a function of \(V\text{.}\) In process \(1\rightarrow 2\) process
Therefore, work in this step will be (with \(n=1\))
In process \(2\rightarrow 3\text{,}\) since \(dV=0\text{,}\) we will have zero work.
In process \(3\rightarrow 4\text{,}\) the equation of the line is
Therefore, work in this step will be
In process \(4\rightarrow 1\text{,}\) since \(dV=0\text{,}\) we will have zero work.
Therefore, work in one cycle will be
This means choice (A) is correct.
(B) We know that processes \(2\rightarrow 3\) and \(4\rightarrow 1\) are isochoric. We need to check if other processes are adiabatic. Let's clculate heat involved in process \(1\rightarrow 2\) and \(3\rightarrow 4\text{.}\) First law for a process says
For monatomic ideal gas
Therefore in process \(1\rightarrow 2\) we get
Hence it is not adiabatic. We do not need to check the other process since we already know that choice (B) is incorrect.
(C) We already calculated \(Q_{12}\text{.}\) Now, we need to calculate \(Q_{23}\text{.}\)
The ratio will be
Hence, (C) is correct.
(D) We need \(Q_{34}\) now.
Hence,
This means (D) is incorrect.
Problem 3.1.20. Q10. Lensmaker's Equation.


\(\frac{1}{f} = (n-1)\left( \frac{1}{R_1} - \frac{1}{R_2} \right)\text{.}\)
(B), (C), (D)
We will need Lensmaker's equation for thin lenses made of material of refractive index \(n\) placed in air.
From this we can get focal length of a plano-convex lens to be
Now, given lens is a composite lens of two plano-convex lenses stacked against each other. Since we are working in thin lens approximation, the inverse of equivalent focal length of the two will be
Therefore, effective focal length will be
Now, we are given \(f\) when \(n_1=n_2=n\text{.}\) That is
and \(f+\Delta f\) when \(n_1=1\) and \(n_2 = n + \Delta n\text{.}\)
We want \(\Delta f/f\text{.}\) Let's take ratio of these two.
Left side is just \(1+ \Delta f/f\text{.}\) Therefore,
Since \(\Delta n \ll n\) we can drop \(\Delta n\) in the denominator of the right side. This gives
(A): Taking absolute value we get
To decide on the answer, we need to check whether the factor on the right side is less than or greater than 1. Since \(1 \lt n \lt 2\) let us replace \(n\) by \(1+\epsilon\text{.}\)
Hence, we find that
which is opposite of the given answer. Hence choice (A) is incorrect.
(B): Using numerical values in Eq. (3.1.8) we get
That is, (B) is correct.
(C): From the negative ssign in Eq. (3.1.8), we see that
That makes (C) correct.
(D): In my derivation of Eq. (3.1.8), \(R\) canceleld out in the ratio. So, not only replacing with concave surface but also any other \(R\) would give the same result as long as thickness \(d \ll R\text{.}\) So, given choice (D) is correct.
Problem 3.1.21. Q11. Dimensional Analysis.
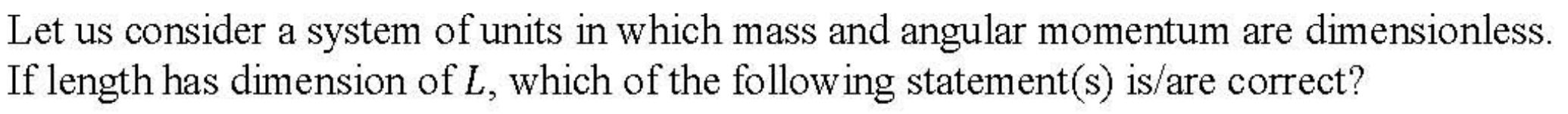
(A), (B), (C).
Since angular momentum of a particle has the formula \(\vec r \times (m \vec v)\text{,}\) we see that
since mass is dimensionless. Hence, dimension of velocity will be one over dimension of length.
Now, since velocity is distance over time, this is
Hence, we find that time has dimension of length squared.
(A): Let's check dimension of momentum.
That is (A) is correct.
(B): Let's check dimension of energy.
That is (B) is correct.
(C): Let's check dimension of force.
That is (C) is correct.
(D): Let's check dimension of power.
That is (D) is incorrect.
Problem 3.1.22. Q12. Ammeter and Voltmeter from a Galvanometer.

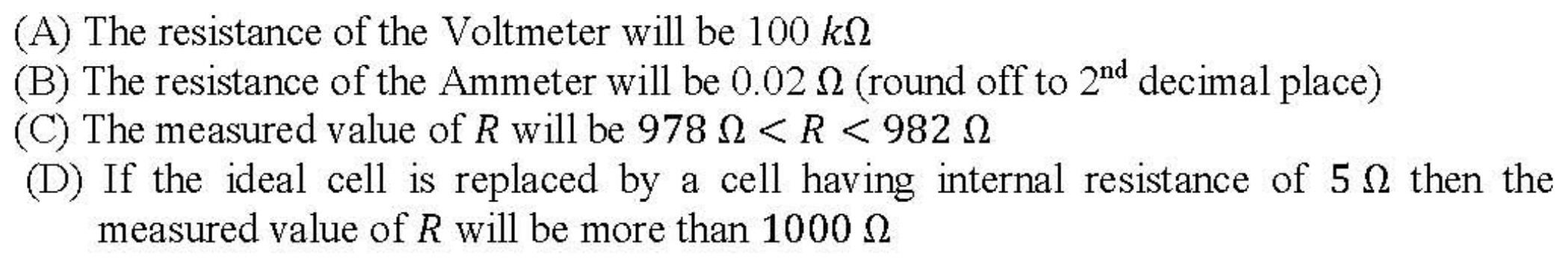
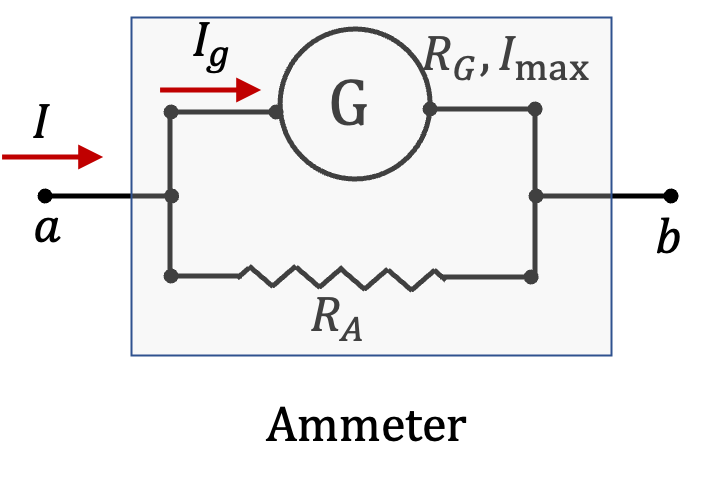
Galvanometer is used as a voltmeter by attaching a suitable resistor in series to the galvanometer. To use a galvanometer as as ammeter, you attach a suitable resistor in parallel to the galavnometer.
(B), (C).
Figure 3.1.23 shows a galvanometer used as ammeter by using an appropriate shunt resistor \(R_A\) and as a voltmeterby using appropriate resistor \(R_V\) in-series.
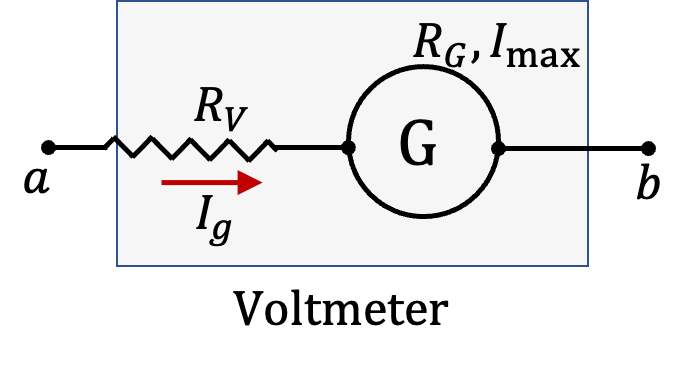
The voltmeter is to read \(100\text{ mV}\) between ends a and b at full deflection, i.e., when current through the galvanometer is max for the galvanometer. Therefore, in the voltmeter, we will have
For the numerical values given,
The ammeter is to read \(I = 1\text{ mA}\text{,}\) when \(I_g=I_\text{max}\text{.}\) Since this is parallel circuit, we will have
Therefore,
For the numerical values given at max displacement in the galvanometer, we get
(A): We found \(R_V = 49,990\, \Omega\text{.}\) Hence, choice (A) is wrong.
(B): We found the same answer for \(R_A\) as given. So, (B) is correct.
(C) & (D): These are for a circuit that measures an unknown resistance by measuring current an voltage readings in an Ohm experiment shown in Figure 3.1.24.
The resistance from this experiment will be ratio of voltmeter reading \((I_1R)\) and ammeter reading \(I = (I_1 + I_2)\text{.}\)
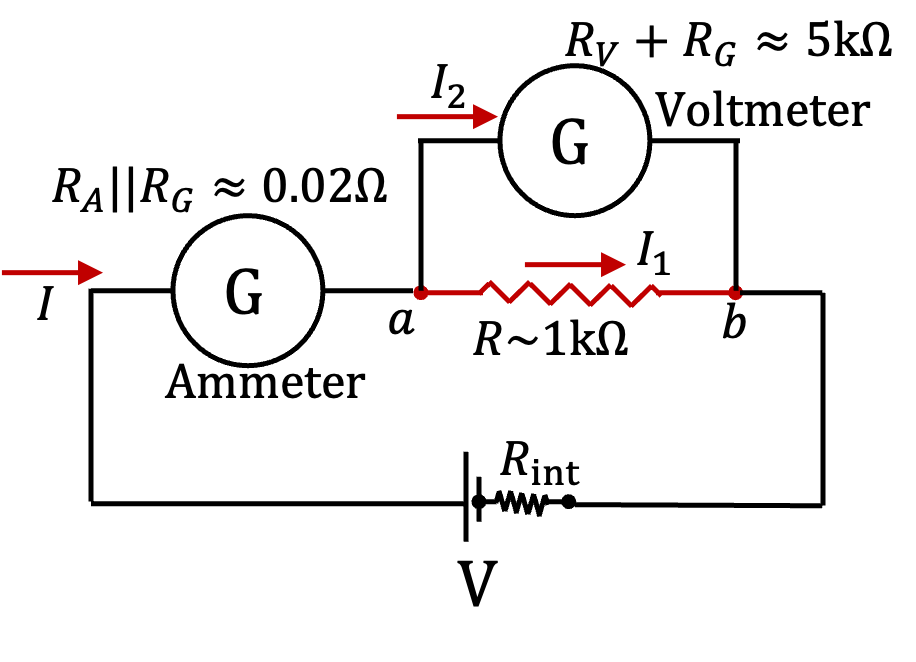
(C) Since current \(I\) divides into two branches, it is immediately clear that
Hence
This is in the range for (C). Hence (C) is correct.
(D): The answer given is incorrect since as shown in (C) above that experimental value of \(R\) depends upon ratio of \(I_1\) and \(I\text{,}\) which is indepdenent of internal resistance.
Problem 3.1.25. Q13. Work from Calculation of a Line Integral.
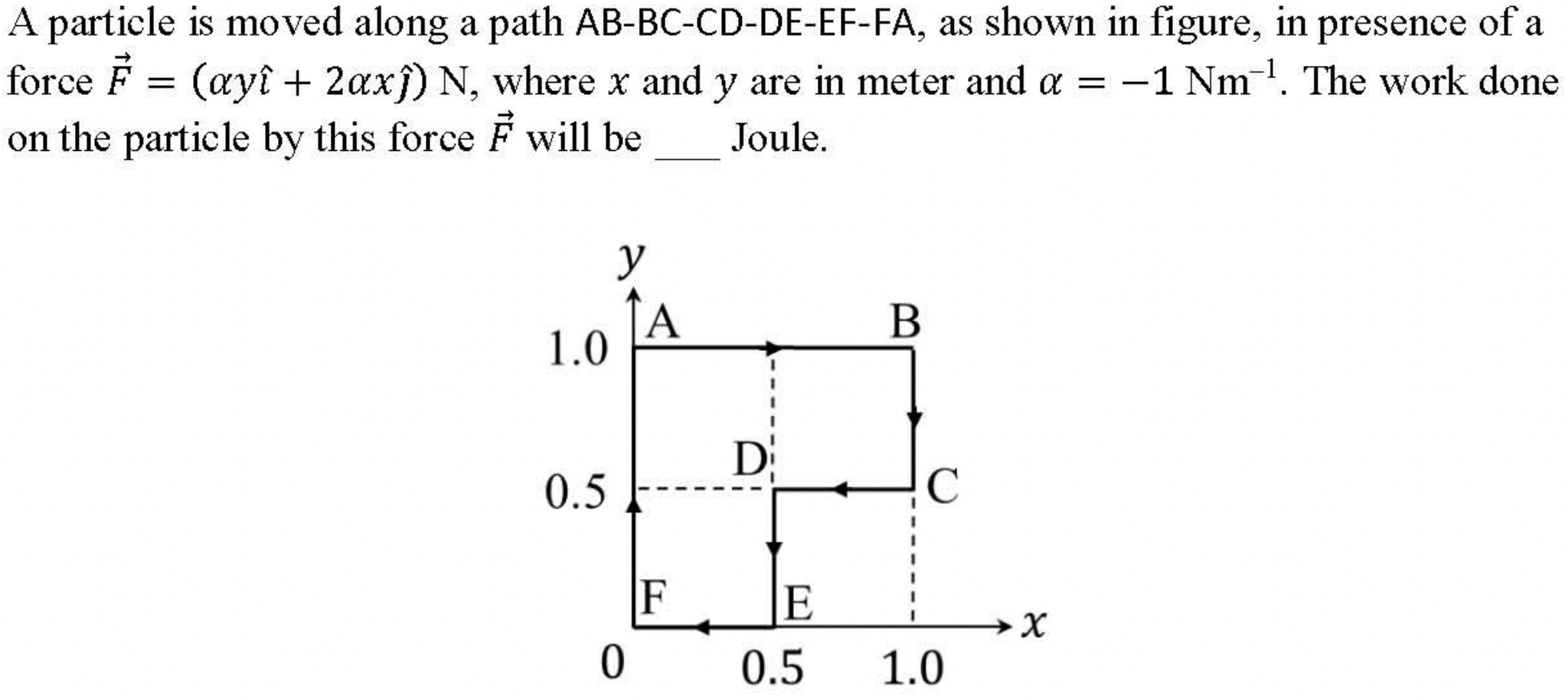
\(W_{if} = \int_i^f \vec F\cdot d\vec r\text{.}\)
\(0.75\text{.}\)
Work in any step is given by the integral
Here,
Therefore,
Now, we carry out calculations for each step.
AB: It has \(dy=0\) and \(y=1\text{.}\) Therefore, from (3.1.9)
BC: It has \(dx=0\) and \(x=1\text{.}\) Therefore,
CD: it has \(dy=0\) and \(y=0.5\text{.}\) Therefore,
DE: It has \(dx=0\) and \(x=0.5\text{.}\) Therefore,
EF: It has \(dy=0\) and \(y=0\text{,}\) which gives \(W_{EF} = 0\text{.}\) We have zero for \(W_FA\) also in a similar way.
Hence, total work for round trip is
Problem 3.1.26. Q14. Stress, Strain, and Young's Modulus.
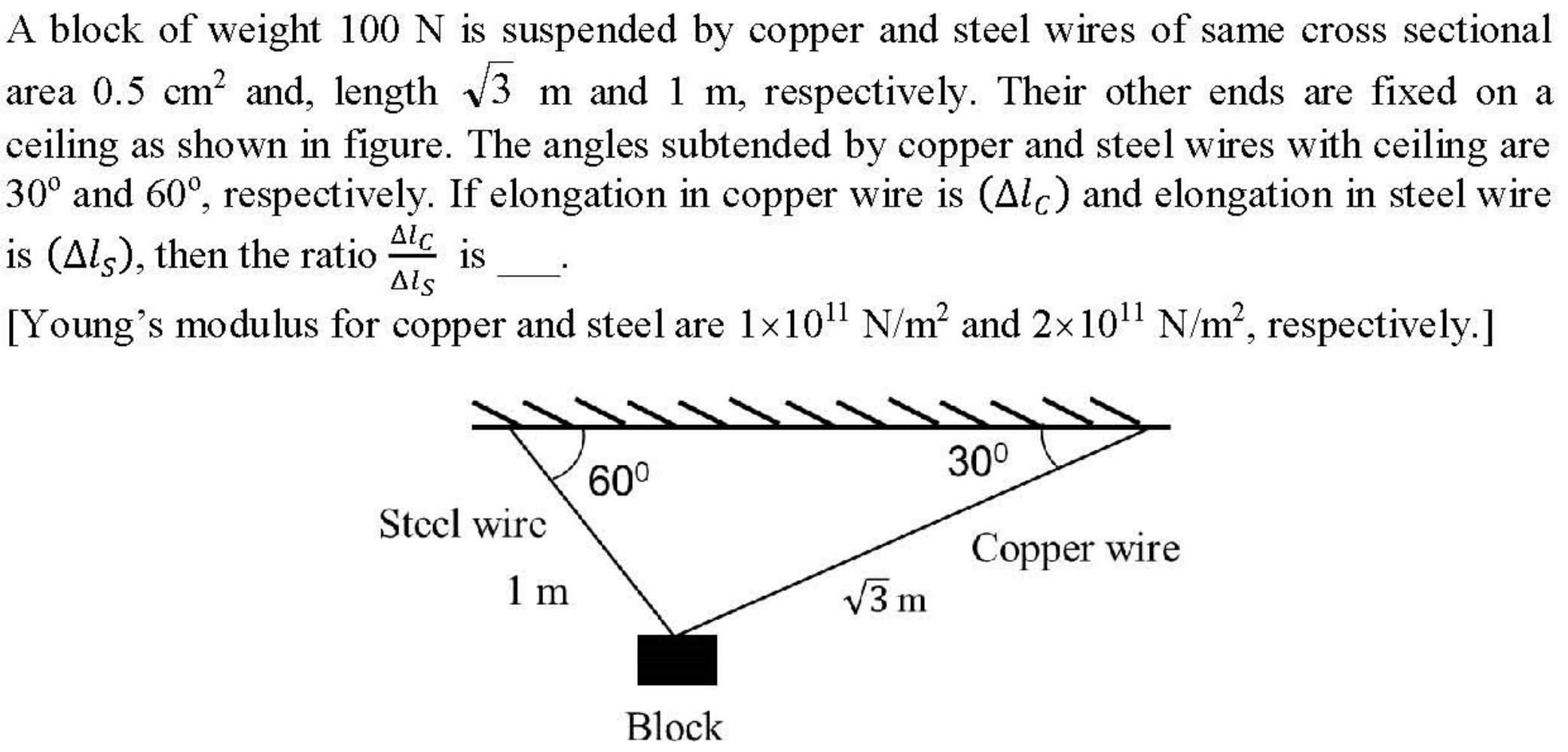
Start from what you need to show and then look for what you need to complete the solution.
\(2.0\text{.}\)
Let \(T_1\) be tension in steel and \(T_2\) the tension in copper cable. Denote by \(l_1\) and \(l_2\) the lengths of steel and copper cables and \(A\) be the area of cross-section of the cables. Since they have the same cross-section, we use one symbol. Then by Hooke's law
Here \(Y_S\) and \(Y_C\) are Young's modulii of steel and copper. Taking ratio of these we get
If we can find \(T_2/T_1\) we will be done. Looking at the balancing of horizontal forces at the knot gives
The other ratios we know are
Using these in Eq. (3.1.10) we get
Problem 3.1.27. Q15. Doppler Effect When Source and Detector Moving at an Angle.
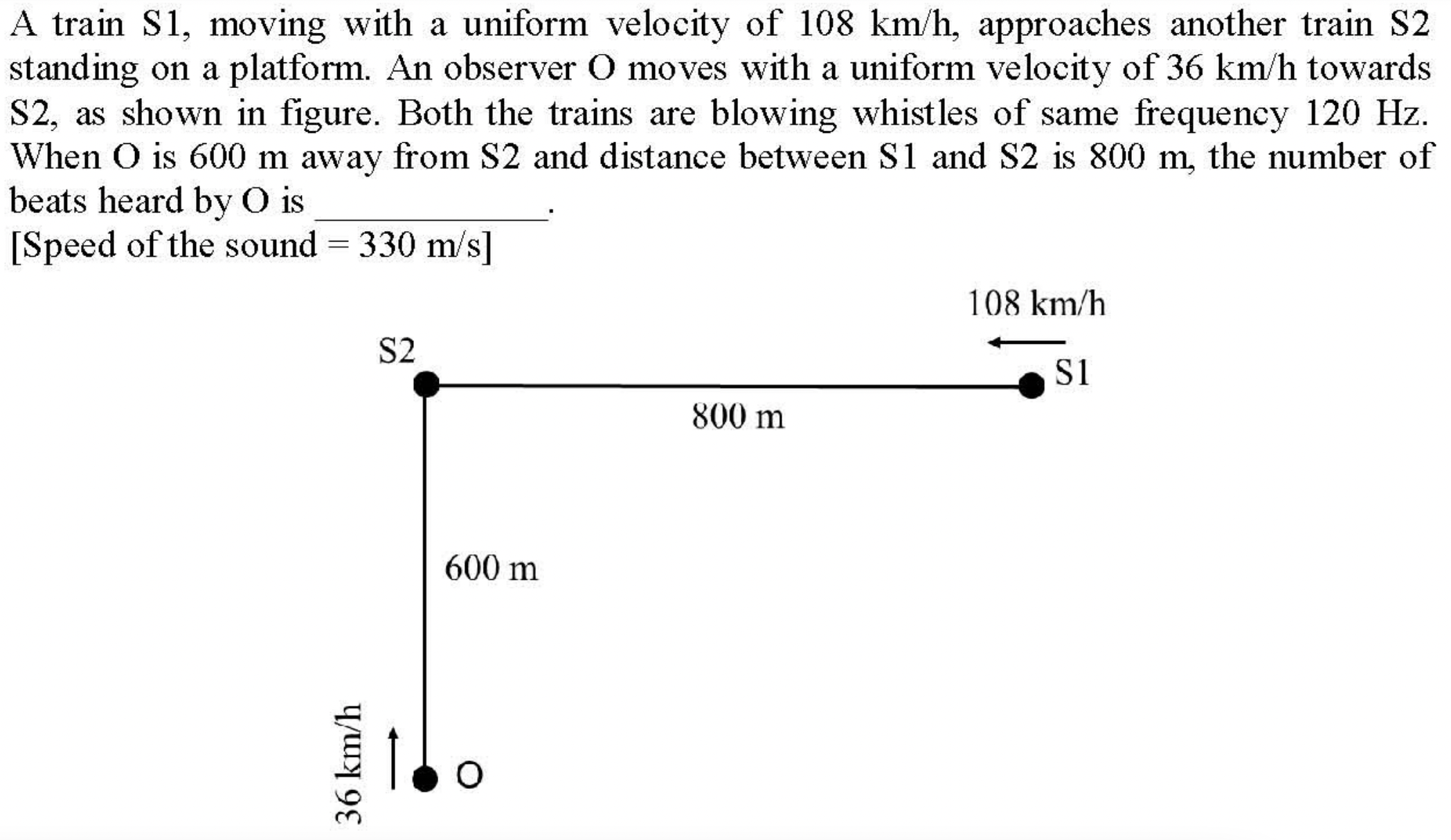
When calculating Doppler effect from S1, project both the source \(v\) and the detector in the direction between source and detector.
8.16\text{ Hz}.
We are dealing with Doppler effect of sound. Let \(v_\text{source}\) be the velocity of the source towards the detector and \(v_\text{detector}\) be velocity of the detector towards the source, both with respect to the medium with convenstion that they are postive for component towards each other. Let \(v\) be thevelocity of the sound in the medium. Then frequency detected will be
The beat frequency of two waves is \(f_\text{beat} = |f_1 - f_2|\text{.}\)
Here it is easier to compute \(f_2\text{,}\) which is
For \(f_1\) we need component of the given velocities in the direction connecting the source and detector. This gives
with \(\sqrt{ 600^2 + 800^2 } = 1000\text{,}\)
Problem 3.1.28. Q16. Capacitor Filled with Infintely Many Dielectric Slabs.
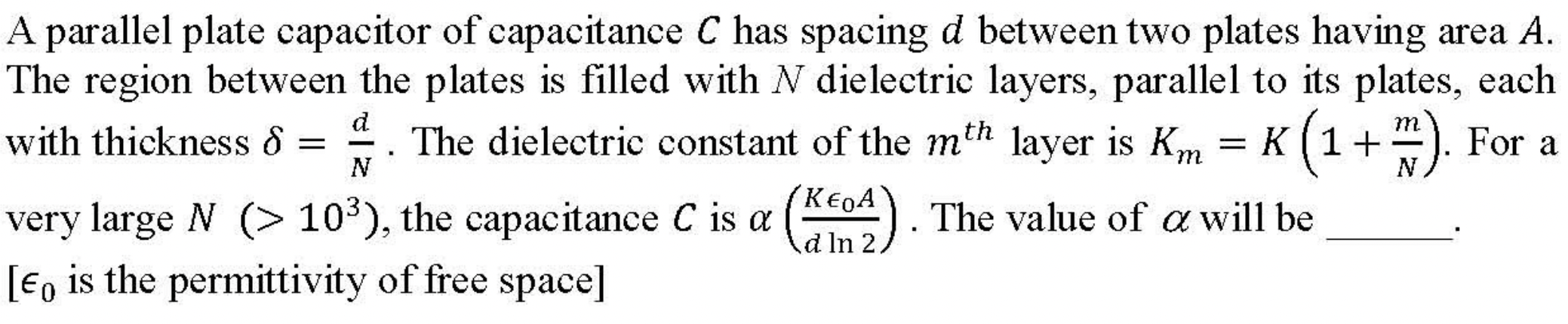
Think of slabs as forming parallel capacitors and then becoming continuous in the \(N\rightarrow\infty\) limit.
1.
This problem is an example of \(N\) capacitors in series with \(m^\text{th}\) capcitor with capacitance
The inverse of equivalent capacitance of \(N\) such capacitors will be
We want the limit of this as \(N\rightarrow \infty\text{.}\)
Let \(x= m/N\text{.}\) With \(N\delta = d\text{,}\) a fixed distance, as \(N\rightarrow \infty\text{,}\) distance between successive \(x\) points become infintisimally small and we can treat \(x\) as a continuous variable. The quantity in \([]\) can be replaced by the following integral.
Hence,
Thus answer in the problem is \(\alpha = 1\text{.}\)
Problem 3.1.29. Q17. Calorimetry.

Set up two equations.
270.
This problem is a problem of just accounting of energy. Let \(L\) denote the latent heat of evaporation and \(C\) the specific heat. Let \(C_0\) be specific heat of calorimeter and \(m_0\) its mass in grams.
First 5 g of liquid goes from \(30^\circ\) to \(80^\circ\) and then evaporates. During this time calorimeter's temperature drops from \(100^\circ\) to \(80^\circ\text{.}\) This gives us one equation.
Now, we have 80 gram of liquid going from \(30^\circ\) to \(50^\circ\) and calorimeter going from \(80^\circ\) to \(50^\circ\text{.}\) This gives
Taking the ratio of these equations we get
The unit is degree celsius.
Problem 3.1.30. Q18. Critical Angle.
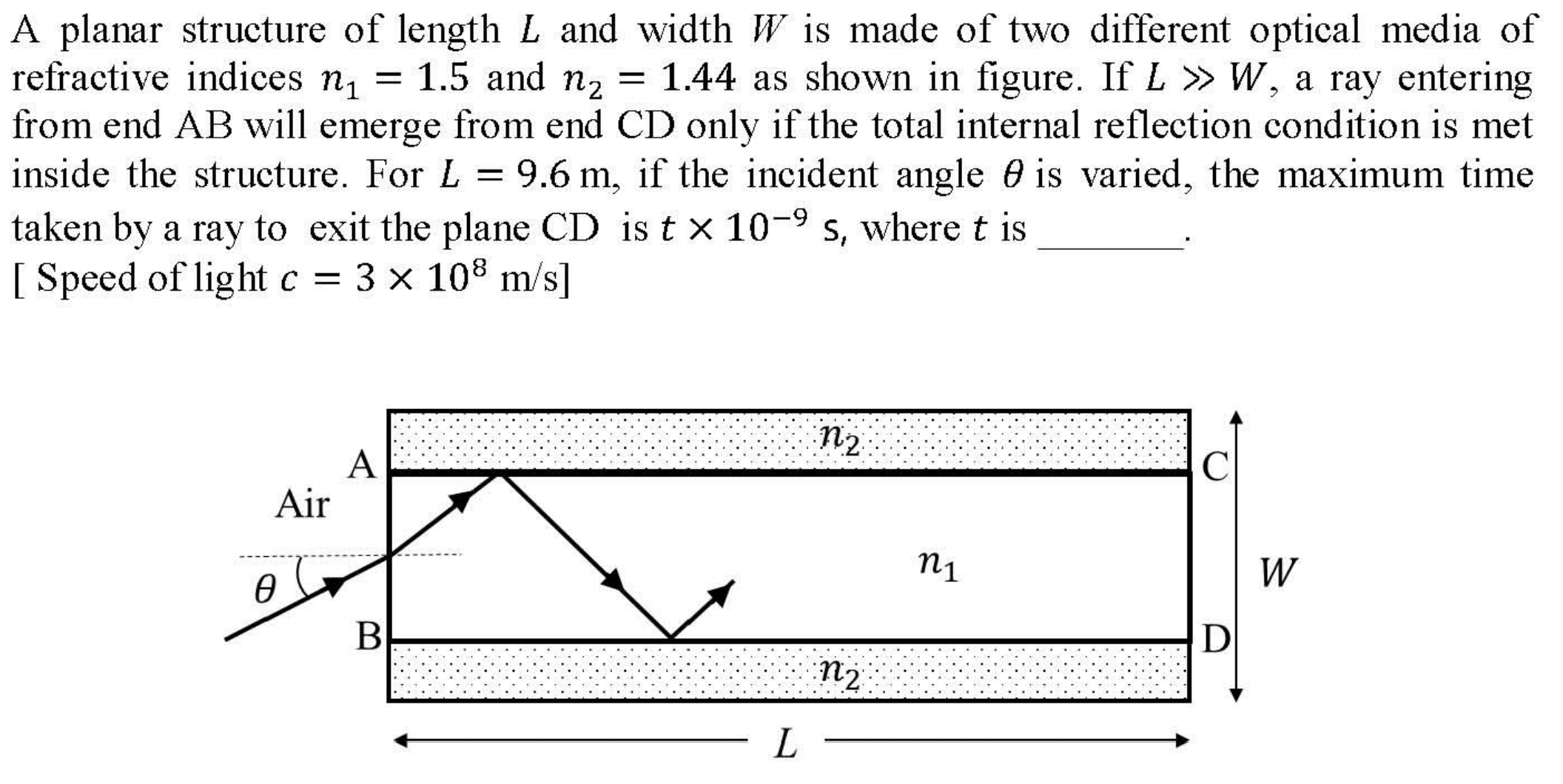
Find \(v\) parallel to the fiber and use that to get \(t\text{.}\)
50.
We want \(\Delta t\) for light traveling a distance \(L\) at speed given by \(v_\parallel\) in the medium of refractive index \(n_1\text{,}\) where
To find \(\cos\theta_1\) we note that max time will correspond to max \(\theta\) in the diagram. That is correspond to max \(\theta_1\) so that reflection at B is a total internal reflection.
Max of \(\theta_1\) will be minimum of \(\theta_2\text{,}\) which has to be the critical angle for \(n_1/n_2\) interface at B. That is at B.
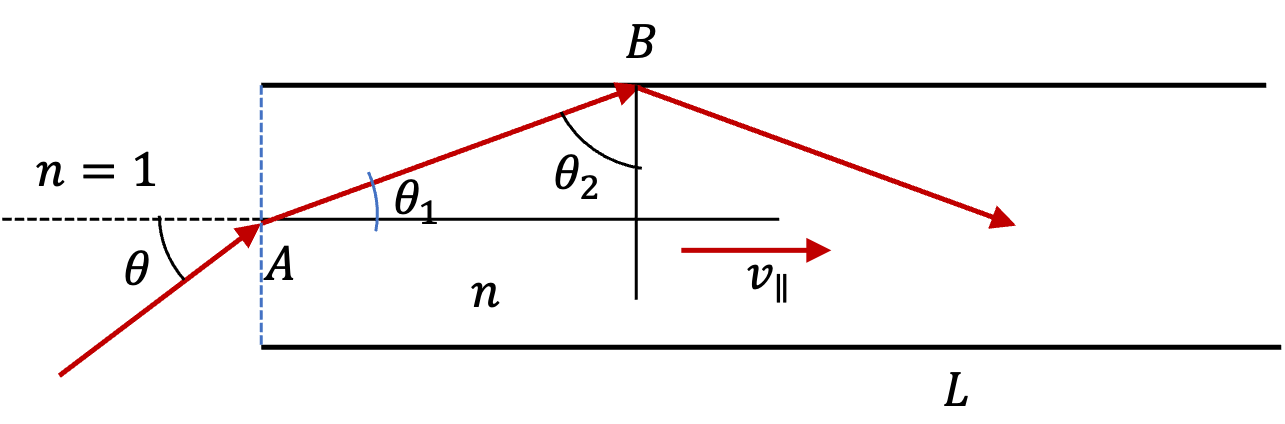
Since \(\theta_1 = 90^\circ - \theta_2\text{,}\) this is
Thus,
Therfore,
