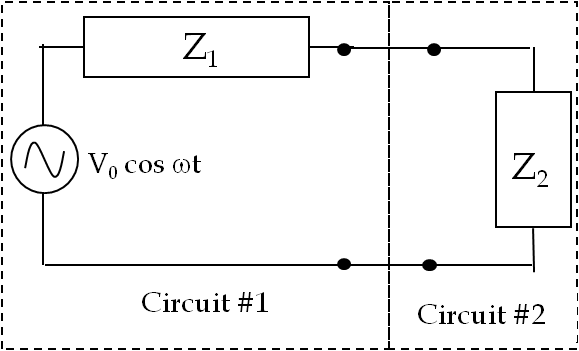
AC Circuit Elements
1. Inductive Reactances.
Follow the link: Example 41.11.
2. Capacitative Reactances.
Follow the link: Example 41.12.
3. Inductive Circuit Example.
Follow the link: Example 41.16.
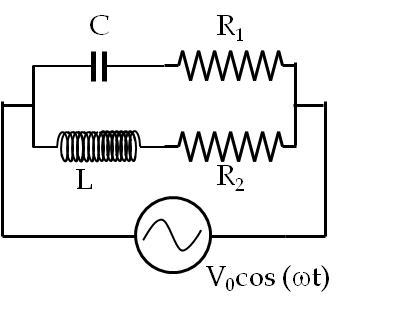
4. RL Circuit with a Sine Voltage Source.
Follow the link: Exercise 41.3.2.1.
5. Current and Voltage Drops Across Resistor and Inductor in Inductive Circuit.
Follow the link: Example 41.17.
6. Capacitative Circuit Example.
Follow the link: Example 41.21.
7. Current in a Capacitative Circuit with Varying Frequency.
Follow the link: Example 41.22.
8. Capacitance of a Starter of a Fluorescent Light Bulb from Current and Voltage.
Follow the link: Exercise 41.4.2.1.
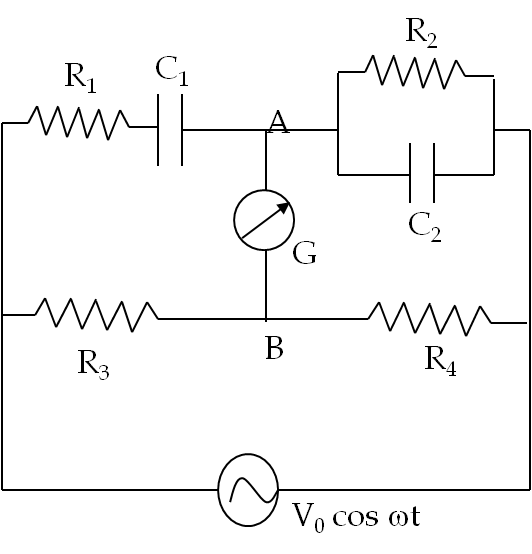
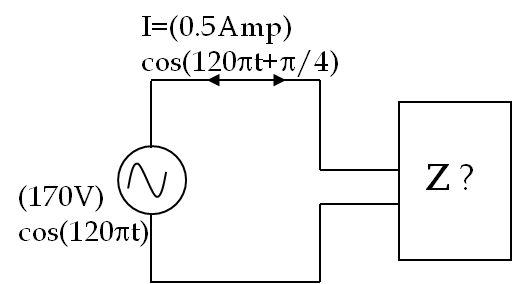
9. Impedance, Current, and Voltages in an RLC circuit.
Follow the link: Example 41.30.
10. Impedance and Phases of Voltages in an RLC Circuit.
Follow the link: Exercise 41.5.2.1.
11. Analysis of an AC RLC Circuit.
Follow the link: Exercise 41.5.2.2.