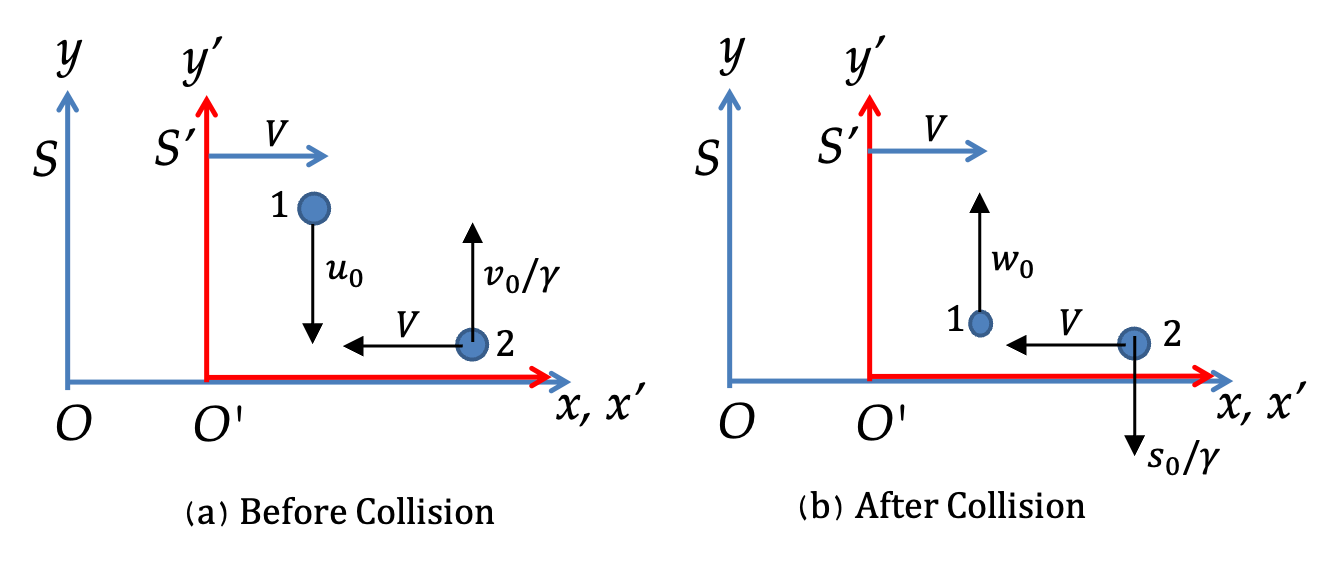
We will carry out an elementary calculation of a two-dimensinal collision in two frames treating mass as an unknown function of speed. Then, we will guess the function that will ensure momentum is conserved in two frames S and S’ that are in relative uniform motion. The setup is shown in
Figure 49.51 where velocities of two particles are shown with respect to frame S’. We assume that the two particles have the same mass when at rest and denote their masses at speed
\(u\) by symbol
\(m_u\text{.}\)
Let us denote velocities before by \(\vec v\) and after by \(\vec w\) with primes for S’ and unprimed for S. Summarizing the data in frame S’, we have
\begin{align*}
\amp \text{Before:} \\
\amp \ \ \ v'_{1x} = 0,\ \ v'_{1y} = -u_0,\ \ v'_{2x} = -V, \ \ v'_{2y} = v_0/\gamma\\
\amp \ \ \ \text{speeds: }\ v'_1 = u_0,\ \ v'_2 = \sqrt{V^2 + v_0^2/\gamma^2 } \\
\amp \ \ \ \text{masses: }\ m_{v'_1},\ \ m_{v'_2}
\end{align*}
\begin{align*}
\amp \text{After:} \\
\amp \ \ \ w'_{1x} = 0,\ \ w'_{1y} = w_0,\ \ w'_{2x} = -V, \ \ w'_{2y} = -s_0/\gamma\\
\amp \ \ \ \text{speeds: }\ w'_1 = w_0,\ \ w'_2 = \sqrt{V^2 + s_0^2/\gamma^2} \\
\amp \ \ \ \text{masses: }\ m_{w'_1},\ \ m_{w'_2}
\end{align*}
These quantities in frame S will be obtained by transforming the velocities.
\begin{align*}
\amp \text{Before:} \\
\amp \ \ \ v_{1x} = V,\ \ v_{1y} = -u_0/\gamma,\ \ v_{2x} = 0, \ \ v_{2y} = v_0\\
\amp \ \ \ \text{speeds: }\ v_1 = \sqrt{V^2 + u_0^2/\gamma^2 } ,\ \ v_2 = v_0 \\
\amp \ \ \ \text{masses: }\ m_{v_1},\ \ m_{v_2}
\end{align*}
\begin{align*}
\amp \text{After:} \\
\amp \ \ \ w_{1x} = V,\ \ w_{1y} = w_0/\gamma,\ \ w_{2x} = 0, \ \ w'_{2y} = -s_0\\
\amp \ \ \ \text{speeds: }\ w_1 = \sqrt{V^2 + w_0^2/\gamma^2},\ \ w_2 =s_0 \\
\amp \ \ \ \text{masses: }\ m_{w_1},\ \ m_{w_2}
\end{align*}
Conservation of momentum along each axis in the two frames are
\begin{align}
S', x:\ \ \amp m_{v'_1}\times 0 + m_{v'_2}(-V) = m_{w'_1}\times 0 + m_{w'_2}(-V) \tag{49.77}\\
S', y:\ \ \amp m_{v'_1}(-u_0) + m_{v'_2}(v_0/\gamma) = m_{w'_1} w_0 + m_{w'_2}(-s_0/\gamma) \tag{49.78}\\
S, x:\ \ \amp m_{v_1}(V) + m_{v_2}\times 0 = m_{w_1}(V) + m_{w_2}\times 0 \tag{49.79}\\
S, y:\ \ \amp m_{v_1}(-u_0/\gamma) + m_{v_2}(v_0) = m_{w_1}(w_0/\gamma) + m_{w_2}(-s_0) \tag{49.80}
\end{align}
\begin{equation}
m_{v'_2} = m_{w'_2}\ \implies\ v'_2 = w'_2 \ \implies\ v_0 = s_0. \tag{49.81}
\end{equation}
\begin{equation}
m_{v_1} = m_{w_1}\ \implies\ v_1 = w_1 \ \implies\ u_0 = w_0.\tag{49.82}
\end{equation}
\begin{equation}
m_{v'_2} \frac{v_0}{\gamma} = m_{u_0} u_0\tag{49.83}
\end{equation}
\begin{equation}
m_{v_2} v_0 = m_{v_1} \frac{u_0}{\gamma}\tag{49.84}
\end{equation}
Now, from these two equations we get
\begin{equation}
\frac{m_{v'_2}} { \gamma m_{v_2} } = \frac{\gamma m_{u_0}}{m_{v_1}}. \tag{49.85}
\end{equation}
Hence, with \(v_2 = v_0\) this simplifies to
\begin{equation}
m_{v_1} m_{v'_2} = \gamma^2 m_{u_0} m_{v_0}.\tag{49.86}
\end{equation}
Here
\begin{equation}
v_1 = \sqrt{V^2 + \frac{u_0^2}{\gamma^2}},\ \ \ v'_2 = \sqrt{V^2 + \frac{v_0^2}{\gamma^2}}.\tag{49.87}
\end{equation}
Now, if we choose
\(v_0 = u_0\text{,}\) then
\(v_1 = v'_2\text{.}\) This simplifies Eq.
(49.86) to
\begin{equation}
m_{v_1} = \gamma m_{u_0}.\tag{49.88}
\end{equation}
With \(u_0=0\text{,}\) this equation gives mass when speed is \(V\text{,}\) \(m_V\text{,}\) in terms of mass at rest, \(m_0\text{,}\) which is also called the rest mass.
\begin{equation}
m_V = \frac{m_0}{\sqrt{ 1- V^2/c^2 }}.\tag{49.89}
\end{equation}
Hence, relativistic momentum of a particle of velocity \(\vec v\) is
\begin{equation}
\vec p = \frac{m_0 \vec v}{\sqrt{ 1- v^2/c^2 }},\ \ \text{or,}\ \ \gamma m_0 \vec v.\tag{49.90}
\end{equation}