Motion in Polar Coordinates

Section 5.5 Motion in Polar Coordinates

Some planar motions are more effectively analyzed in a different coordinate system than the Cartesian coordinates. Polar coordinates are more natural for circular and elliptical trajectories. In this section, we will introduce polar coordinates and define new unit vectors for analysing vectors.

Subsection 5.5.1 The Polar Coordinates

Refer to Fig. Figure 5.31 that shows a description of point P in Cartesian and polar coordinates. To specify the position of P, we could equally state as \((x, y) \) or as \((r,\, \theta)\text{.}\) The radial coordinate \(r\) is the direct distance from the origin and the angular coordinate \(\theta \) the angle from the positive \(x \) axis. If the direction OP is counterclockwise, \(\theta \) is positive, and if clockwise, then \(\theta \) is negative.

Figure 5.31. Polar coordinates \(r \) and \(\theta\text{.}\) The right-angled triangle \(\triangle OPX\) shows the relation between the Cartesian coordinates \((x,y)\) and polar coordinates \((r,\theta)\) for the same point P. Clearly, \(x = r \cos\, \theta \text{,}\) \(y = r \sin\, \theta \text{,}\) \(r = \sqrt{x^2 + y^2}\text{,}\) and \(\tan\, \theta = y/x\text{.}\)

You can see that the polar coordinates are simply the magnitude \(r\) and direction \(\theta \) of the position vector \(\vec r\text{.}\) The relations between the polar coordinates \((r,\theta)\) and the Cartesian coordinates \((x,y)\) for the same point are

\begin{align} \amp x = r\, \cos\,\theta, \tag{5.13}\\ \amp y = r\, \sin\,\theta, \tag{5.14}\\ \amp r = \sqrt{x^2+y^2}, \tag{5.15}\\ \amp \theta = \tan^{-1}\left(\dfrac{y}{x} \right) \tag{5.16} \end{align}

Note that \(\theta \) obtained using the \(\tan^{-1}\) function will need to be adjusted for the quadrant in which \((x,y) \) resides: add \(\pi \text{ rad}\) if \((x,y) \) is in quadrant 2 or 3 and \(2\pi \text{ rad}\) if \((x,y) \) is in quadrant 4.

Polar coordinates \((r,\theta)\) in the \(xy \) plane together with the Cartesian \(z \) are the Cylindrical coordinates. The cylindrical coordinate system is useful for studying physics of systems that have a rotational symmetry about the \(z\) axis. We will study Cylindrical coordinates more later in the book.

Example 5.32. Cartesian to Polar Coordinates.

Convert the following Cartesian coordinates \((x,y)\) into polar coordinates.

\((0,1)\text{;}\)
\((1,0)\text{;}\)
\((-1,0)\text{;}\)
\((0,-1)\text{;}\)
\((3,4)\text{;}\)
\((-3,4)\text{;}\)
\((-3,-4)\text{;}\)
\((3,-4)\text{.}\)

Answer.

See solution.

Solution.

Answers are

\(r = 1\text{,}\) \(\theta = \pi/2\)
\(r = 1\text{,}\) \(\theta = 0\)
\(r = 1\text{,}\) \(\theta = -\pi\)
\(r = 1\text{,}\) \(\theta = -\dfrac{3}{2}\pi\)
\(r = 5\text{,}\) \(\theta = \tan^{-1}({4/3}) = 53^\circ\)
\(r = 5\text{,}\) \(\theta = \tan^{-1}({4/-3}) = -53^\circ\) clockwise from negative \(x\) axis.
\(r = 5\text{,}\) \(\theta = \tan^{-1}({-4/-3}) = 53^\circ\) counterclockwise from negative \(x\) axis.
\(r = 5\text{,}\) \(\theta = \tan^{-1}({-4/3}) = -53^\circ\) clockwise from positive \(x\) axis.

Example 5.33. Polar to Cartesian Coordinates.

Convert the following polar coordinates \((r,\theta)\) into Cartesian coordinates. The angle is given in radians counterclockwise from the positive \(x\)-axis as seen from the side of the positive \(z\)-axis.

\((1,0)\text{;}\)
\((1,\pi/3)\text{;}\)
\((1,2\pi/3)\text{;}\)
\((1,3\pi/3)\text{;}\)
\((1,4\pi/3)\text{;}\)
\((1,5\pi/3)\text{;}\)
\((1,6\pi/3)\text{;}\)
\((2,29\pi/3)\text{.}\)

Answer.

See solution.

Solution.

Answers are

\(x = 1.0\text{,}\) \(y=0\)
\(x = 0.5\text{,}\) \(y=0.866\)
\(x = -0.5\text{,}\) \(y=0.866\)
\(x = -1.0\text{,}\) \(y=0\)
\(x = -0.5\text{,}\) \(y=-0.866\)
\(x = 0.5\text{,}\) \(y=.866\)
\(x = 1.0\text{,}\) \(y=0\)
\(x = -0.736\text{,}\) \(y=0.677\)

Subsection 5.5.2 Unit Vectors \(\hat u_r\) and \(\hat u_\theta\)

The radial and tangential directions are important in circular motion as we saw in the separation of acceleration of an object moving in a circle into the centripetal and tangential accelerations. When studying circular motion, we used radially inward direction towards center to denote the centripetal part of acceleration. Here, in polar coordinates, we will use radially outward direction to define corresponding radial component.

To simplify vector algebra for polar coodinates, we take advantage of unit vectors along the radial and tangential directions, as we did with analyzing vectors in Cartesian coordinates with \(\hat i\) and \(\hat j\text{.}\) They are also called unit vectors of the polar coordinate system.

Subsubsection 5.5.2.1 Definition of \(\hat u_r\) and \(\hat u_\theta\)

The polar coordinate unit vectors, denoted by \(\hat u_r\) and \(\hat u_\theta\text{,}\) respectively, are shown in Figure 5.34. We can write \(\hat u_r\) in terms of \(\hat i\) and \(\hat j\text{.}\)

\begin{equation} \hat u_r = (\cos\theta)\; \hat i+ (\sin\theta)\;\hat j.\tag{5.17} \end{equation}

The unit vector \(\hat u_\theta\) is just \(\hat u_r\) rotated \(90^{\circ}\text{,}\) therefore, by substituting \(\theta \) by \(\theta + \pi/2 \) in above gives

\begin{equation} \hat u_\theta = -(\sin\theta)\; \hat i+ (\cos\theta)\; \hat j.\tag{5.18} \end{equation}

Unlike the \(\hat i\) and \(\hat j\text{,}\) the polar unit vectors \(\hat u_r \) and \(\hat u_\theta \) depend on angle \(\theta \) of the location of object P. You might say that, while we have just one pair, i.e., \((\hat i,\ \hat j)\text{,}\) in the Cartesian system, we have infinitely many unit vector pairs \(\left( \hat u_r,\ \hat u_\theta\right) \) in the polar system, one pair for each value of \(\theta\text{.}\)

You may find in other books that the vectors \(\hat u_r \) and \(\hat u_{\theta}\) are denoted as simply \(\hat r \) and \(\hat\theta\text{.}\) For pedagogical reasons I will continue with our notation, although at times it may appear too cumbersome to write \(u\) all the time and you may want to use simpler notation; just make sure you do not confude \(\hat r\) with distance \(r\) and similarly for \(\hat\theta\) and \(\theta\text{.}\)

Subsubsection 5.5.2.2 \(\hat u_r\) and \(\hat u_\theta \) as Basis Vectors

Recall that \(\hat i\) and \(\hat j\) are sufficient to express any arbitrary vector \(\vec v\) in \(xy\)-plane.

\begin{equation*} \vec v = v_x\; \hat i + v_y\; \hat j. \end{equation*}

We say that \(\hat i\) and \(\hat j\) form a basis for \(xy\)-plane. \(\hat i\) and \(\hat j\) are further characterized by their length being \(1\) and their dot product being zero, i.e., they are perpendicular. Perpendicular vectors are also called orthogonal to each other. Vectors whose length equal 1 are called normalized. Thus, \(\hat i\) and \(\hat j\) are a set of orthonormal vectors in \(xy\)-plane.

Similar to \(\hat i\) and \(\hat j\text{,}\) the radial and tangential vectors \(\hat u_r\) and \(\hat u_\theta \) are orthogonal and hence, they also form a basis for \(xy\)-plane. Since, their lengths are also equal to 1, they are a pair of orthonormal vectors.

\begin{equation*} \hat u_r \cdot \hat u_\theta = 0,\ \ |\hat u_r|=1,\ \ |\hat u_\theta|=1. \end{equation*}

An arbitrary vector \(\vec v\) expressed in terms of unit vectors of the polar coordinates is written as

\begin{equation*} \vec v = v_r\; \hat u_r + v_\theta\; \hat u_\theta. \end{equation*}

Here \(v_r\) is radial component of \(\vec v\) and \(v_\theta\) is tangential component.

Just as taking the dot product of vector \(\vec v\) with \(\hat i\) or \(\hat j\) gives us the corresponding Cartesian component,

\begin{equation*} v_x = \vec v \cdot \hat i,\ \ v_y = \vec v \cdot \hat j, \end{equation*}

we can get the radial and tangential components similarly by an appropriate dot product.

\begin{equation*} v_r = \vec v \cdot \hat u_r,\ \ v_\theta = \vec v \cdot \hat u_\theta. \end{equation*}

Subsubsection 5.5.2.3 Relation Among Components in \((\hat i, \hat j)\) and \((\hat u_r, \hat u_\theta)\) Bases

We start with first noting that we can also write \(\hat i\) and \(\hat j\) in terms of \(\hat u_r \) and \(\hat u_\theta\text{,}\) just by reversing the definition of \(\hat u_r \) and \(\hat u_\theta\text{.}\)

\begin{align} \amp \hat i= (\cos\theta)\; \hat u_r -(\sin\theta)\; \hat u_\theta,\tag{5.19}\\ \amp \hat j= (\sin\theta)\; \hat u_r + (\cos\theta)\; \hat u_\theta.\tag{5.20} \end{align}

By using Eqs. (5.19) and (5.20) we can replace \(\hat i\) and \(\hat j\) in terms of \(\hat u_r \) and \(\hat u_{\theta}\) in any arbitrary vector written in Cartesian components.

\begin{align} \vec A\amp = A_x \hat i+ A_y \hat j\tag{5.21}\\ \amp = A_x \left( \cos\theta\ \hat u_r - \sin\theta\ \hat u_{\theta} \right) + A_y \left(\sin\theta\ \hat u_r + \cos\theta\ \hat u_{\theta} \right)\tag{5.22}\\ \amp = \left( A_x \cos\theta\ + A_y \sin\theta\ \right) \hat u_r + \left( -A_x \sin\theta\ + A_y\cos\theta\ \right)\hat u_{\theta}\tag{5.23}\\ \amp = A_r\;\hat u_r + A_\theta\;\hat u_{\theta}\tag{5.24} \end{align}

Therefore,

\begin{align} \amp A_r = A_x \cos\theta\ + A_y \sin\theta,\tag{5.25}\\ \amp A_{\theta} = -A_x \sin\theta\ + A_y\cos\theta.\tag{5.26} \end{align}

Example 5.35. Unit Vector \(\hat u_r\).

(a) Draw the unit vector \(\hat u_r\) for the following rays. The rays are specified by the angles they make with the positive \(x\)-axis. (i) \(\theta = 0\text{,}\) (ii) \(\theta = \pi/3\text{,}\) (ii) \(\theta = 2\pi/3\text{,}\) (iv) \(\theta = 3\pi/3\text{,}\) (v) \(\theta = 4\pi/3\text{,}\) (vi) \(\theta = 5\pi/3\) , (vii) \(\theta = 6\pi/3\text{.}\) (b) Give the expression of these unit vectors in terms of the unit vectors \(\{\hat i, \hat j\}\) along the Cartesian axes.

Answer.

(b) \(\hat u_r = \cos\theta\ \hat i + \sin\theta\ \hat j\) for different value of \(\theta\text{.}\)

Solution 1. a

The unit vectors in different directions fall on the unit circle as shown in Figure 5.36.

Figure 5.36. Figure for Example 5.35(a).

Solution 2. b

The \(x\)- and \(y\)-components of unit radial vector in the direction of counterclockwise angle \(\theta\) from the positive \(x\) axis is given by

\begin{equation*} \hat u_r = \cos\theta\ \hat i + \sin\theta\ \hat j \end{equation*}

We would substitute the value for \(theta\) for each of the rays to find the representation of the unit radial vector in that direction. For instance, the case (ii) when \(\theta = \pi/3\) is

\begin{align*} \hat u_r \amp = \cos(\pi/3)\ \hat i + \sin(\pi/3)\ \hat j\\ \amp = \frac{1}{2}\ \hat i + \frac{\sqrt{3}}{2}\ \hat j. \end{align*}

Checkpoint 5.37. Express Cartesian Components in terms of Polar Components.

In Eqs. (5.25) and (5.26), we have \(A_r\) and \(A_\theta\) in terms of \(A_x\) and \(A_y\text{.}\) Now, do the other way - find expressions of \(A_x\) and \(A_y\) in terms of \(A_r\) and \(A_\theta\text{.}\)

Subsection 5.5.3 (Calculus) Position, Velocity, Acceleration

Subsubsection 5.5.3.1 Position

The position of a particle is vector \(\vec r\) with magnitude \(r \text{,}\) which is the radial coordnate, and the direction is given by \(\theta \text{,}\) which is the angular coordinate of the polar coordinate system. We could also write this very simply if we use the unit vector \(\hat u_r \text{.}\)

\begin{equation} \vec r = r\, \hat u_r.\tag{5.27} \end{equation}

Subsubsection 5.5.3.2 Displacement and Distance on Trajectory

An infinitesimal displacement on the trajectory of motion can be obtained by comparing position vectors of nearby points on the trajectory. Figure 5.38 shows infinitesimal displacement vector \(d\vec r\) whose direction will be tangential to the trajectory, i.e., the direction of velocity at that instant.

We can work out the magnitude of \(d\vec r\) by imagining a circle centered at the origin with radius \((r = |\vec r|)\) and we seek arc length on that circle.

\begin{equation} |d\vec r| = r d\theta.\tag{5.28} \end{equation}

To find the distance travel on the trajectory between instant \(t_1\) and instant \(t_2\text{,}\) we just have to integrate the length of infinitesimal vector. Informally, we can write this as

\begin{equation*} \text{Distance} = \int r d\theta. \end{equation*}

To convert this to an integral over time we will do the following.

\begin{equation*} \text{Distance} = \int_{t_1}^{t_2} r \frac{d\theta}{dt}\; dt. \end{equation*}

The displacement between \(t_1\) and \(t_2\) will be a formal integral of the infinitesimal displacment vector.

\begin{equation*} \text{Displacment} = \int d\vec r. \end{equation*}

Subsubsection 5.5.3.3 Velocity.

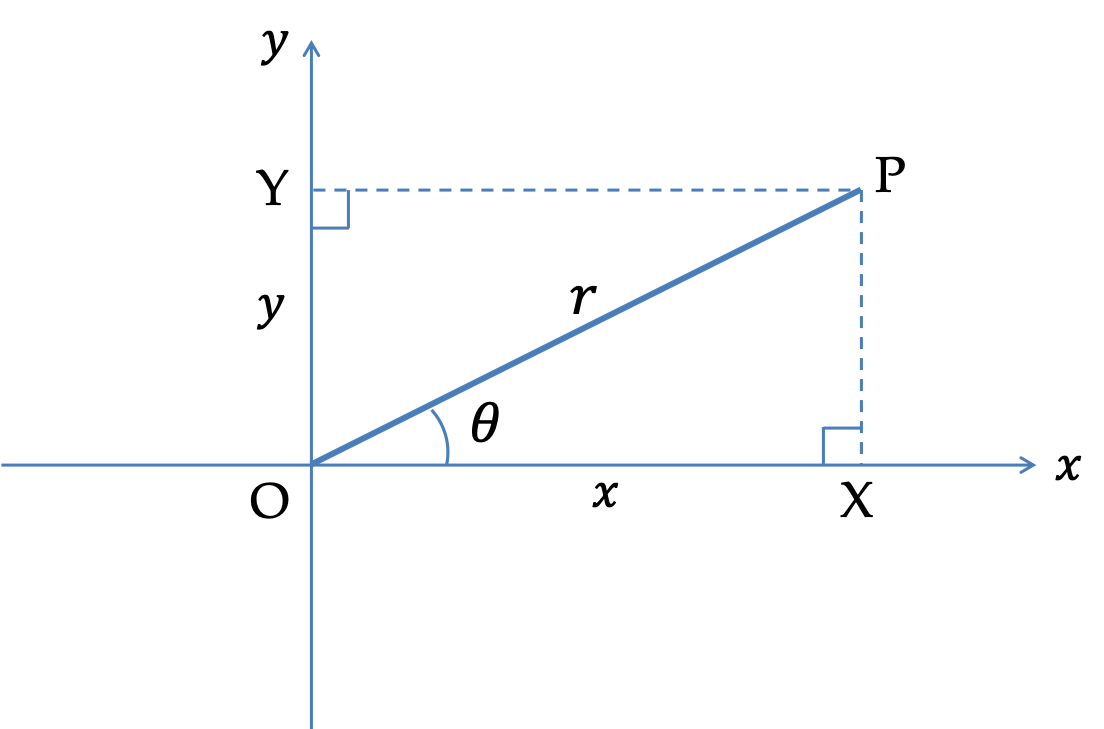
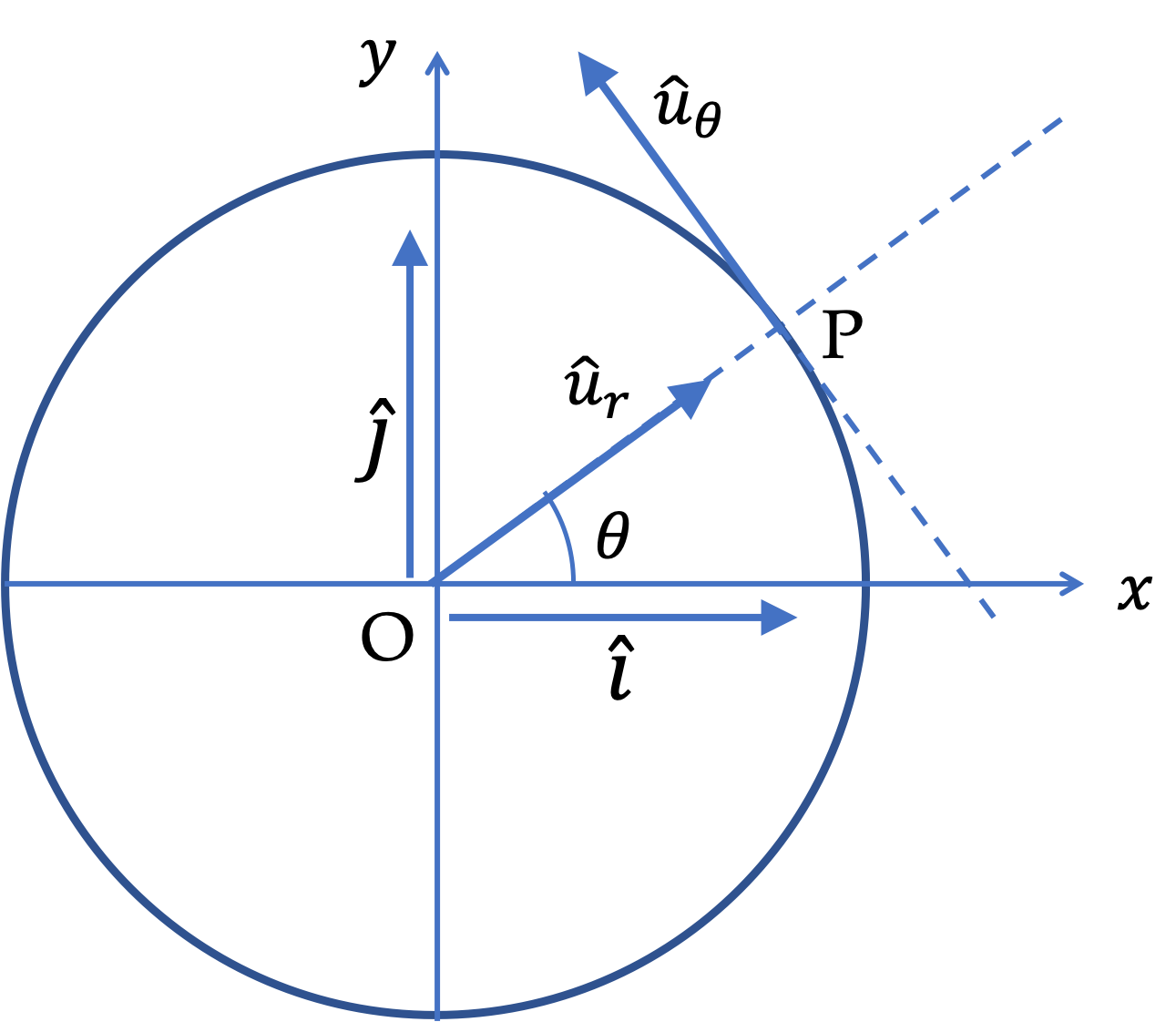
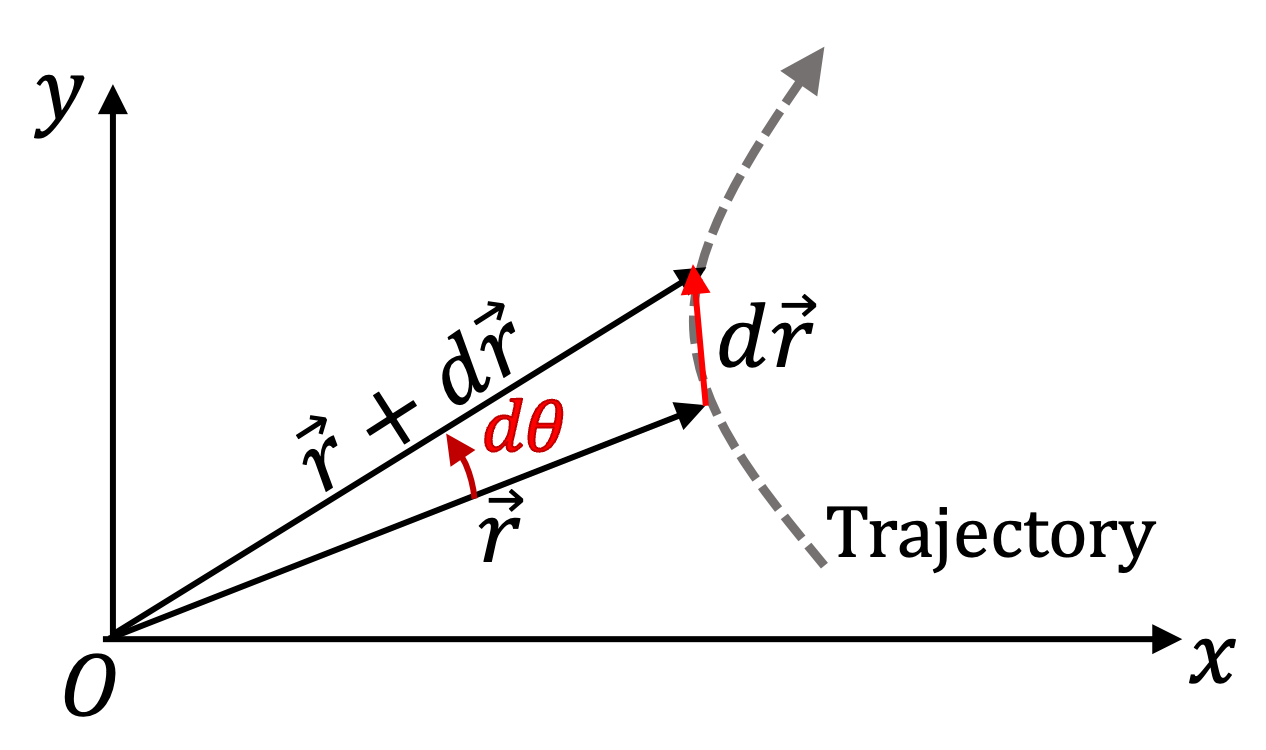
Velocity is the derivative of position vector.

\begin{equation*} \vec v = \dfrac{d\vec r}{dt}. \end{equation*}

If we use Eq. (5.27), we would get

\begin{equation*} \vec v = \dfrac{d }{dt}\left( r\, \hat u_r \right). \end{equation*}

Expanding the right side, using the product rule,

\begin{equation} \vec v = \frac{d r}{dt}\, \hat u_r + r\, \frac{d \hat u_r}{dt}.\tag{5.29} \end{equation}

We are now stuck since

\begin{equation*} \frac{d \hat u_r}{dt} \ne 0, \end{equation*}

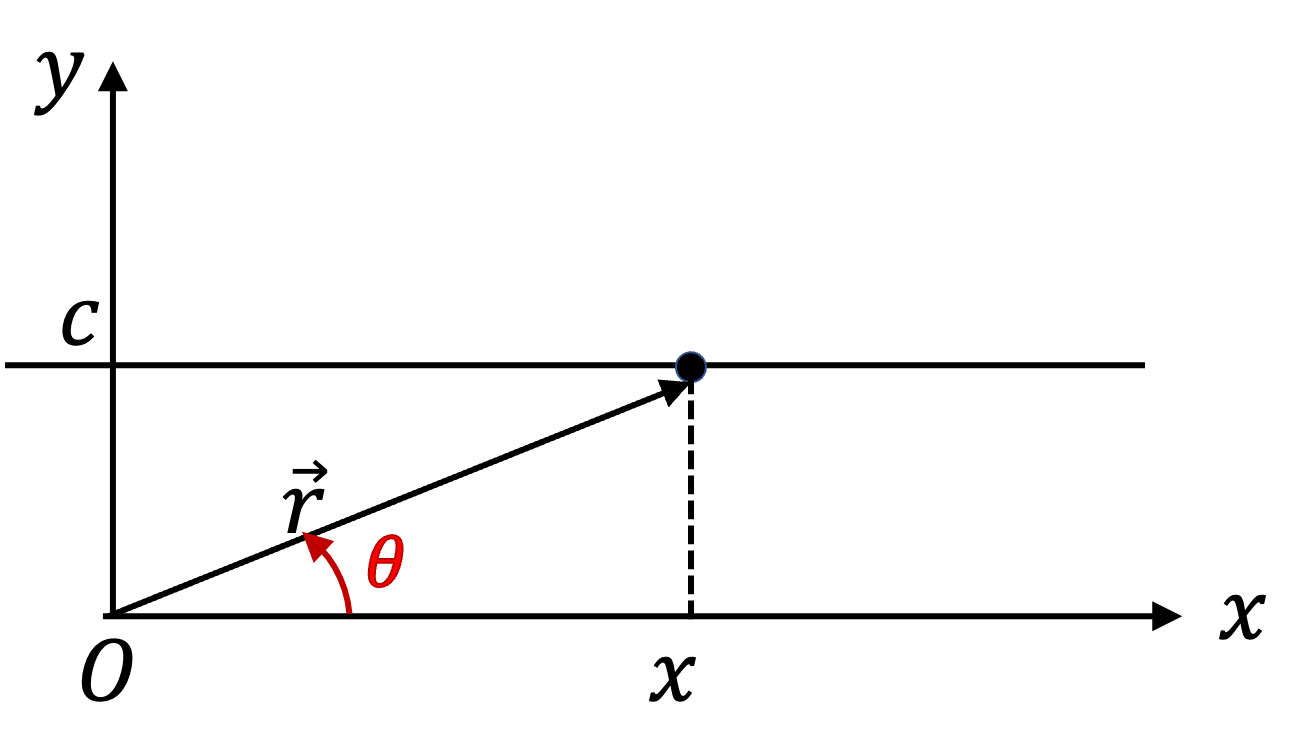
since \(\hat u_r \) depends on the direction of the position, which is a time-dependent. However, the Cartesian unit vecotrs \(\hat i\) and \(\hat j\) are independent of position, i.e.,

\begin{equation} \frac{d \hat i}{dt} = 0,\ \ \ \frac{d \hat j}{dt} = 0.\tag{5.30} \end{equation}

That means, to evaluate \(\dfrac{d \hat u_r}{dt}\text{,}\) we should work with the expression of \(\hat u_r\) in terms of \(\hat i\) and \(\hat j\text{.}\)

\begin{align*} \dfrac{d \hat u_r}{dt} \amp = \dfrac{d }{dt} \left(\cos\theta\, \hat i+ \sin\theta\, \hat j\right),\\ \amp = \left(-\sin\theta\, \hat i+ \cos\theta\, \hat j\right) \dfrac{d\theta}{dt}.\\ \amp = \left(\frac{d\theta}{dt}\right)\, \hat u_\theta. \end{align*}

The derivative \(d\theta/dt\) gives us the rate at which the angular variable changes, and therefore, it is called the angular velocity. It is denoted by the small “omega”, \(\omega\text{.}\)

\begin{equation} \omega = \frac{d\theta}{dt}.\tag{5.31} \end{equation}

Therefore, the velocity in Eq. (5.29) will be

\begin{equation} \vec v = \frac{d r}{dt}\, \hat u_r + \omega\, r\, \hat u_\theta.\tag{5.32} \end{equation}

It is also helpful to introduce the notation for the rate of change of the radial coordinate \(r \text{:}\)

\begin{equation} v_r = \frac{dr}{dt}.\tag{5.33} \end{equation}

This is called radial velocity. The product \(\omega\, r \) is the tangential velocity, denoted by \(v_\theta\text{.}\)

\begin{equation} v_\theta = \omega\, r.\tag{5.34} \end{equation}

Finally, we get a simple expression for the velocity

\begin{equation} \vec v = v_r\, \hat u_r + v_\theta\, \hat u_\theta.\tag{5.35} \end{equation}

Case of Circular Motion:

\(\)

When motion happend in a circle of radius R. Then, the radial variable is fixed in time. This gives

\begin{equation*} v_r = \dfrac{dr}{dt} = 0. \end{equation*}

Therefore, we will get the velocity as

\begin{equation*} \vec v = \omega\, R\, \hat u_\theta. \end{equation*}

That is velocity is tangential, and directed in the \(\hat u_\theta\) direction for the counterclockwise motion, and in the \(-\hat u_\theta \) direction for a clockwise motion, with magnitude, \(v=|\omega\, R|\text{,}\) i.e., the speed \(v\text{.}\)

Subsubsection 5.5.3.4 (Calculus) Acceleration

Acceleration is derivative of velocity. Therefore,

\begin{equation} \vec a = \dfrac{d}{dt}\left( v_r\, \hat u_r + \omega\, r\, \hat u_\theta\right).\tag{5.36} \end{equation}

Carrying out the calculations as we have done for velocity, i.e., expressing \(\hat u_r\) and \(\hat u_\theta\) in terms of \(\hat i\) and \(\hat j\text{,}\) and expanding the derivatives, and simplifying we get

\begin{align*} \vec a\amp = \left[ \frac{dv_r}{dt} - r\, \omega^2 \right]\hat u_r + \left[2 v_r\, \omega + r\left( \frac{d \omega}{dt}\right) \right]\hat u_{\theta}. \end{align*}

This gives the radial and angular components of the acceleration vector \(\vec a \) as

\begin{align} \amp a_r = \frac{dv_r}{dt} - r\, \omega^2. \tag{5.37}\\ \amp a_{\theta} = 2 v_r\, \omega + r\left( \frac{d \omega}{dt}\right) .\tag{5.38} \end{align}

In the case of circular motions, \(a_r\) and \(a_{\theta}\) are also called (negative of) centripetal and tangential accelerations respectively.

Case of Circular Motion:

\(\)

For a circular motion, \(r \) is fixed making its derivative equal to zero.

\begin{equation*} r = R,\ \ \ v_r = \dfrac{dr}{dt} = 0. \end{equation*}

Therefore,

\begin{align*} \amp a_r = - R\, \omega^2. \\ \amp a_{\theta} = R\left( \frac{d \omega}{dt}\right). \end{align*}

Notice the negative sign in the radial part \(a_r \text{;}\) this indicates that the radial accceleration is pointed towards the center, which is why \(R\omega^2\) is the centripetal acceleration, \(a_c \text{.}\) If we substitute \(\omega = v/R\) where \(v \) is the speed, then

\begin{equation*} a_c = -a_r = R\, \omega^2 = \dfrac{v^2}{R}. \end{equation*}

The tangential component \(a_{\theta} \) is the tangential acceleration, which, for a coounterclockwise motion, is positive for increasing speed and negative for decreasing speed. It can be also written using the rate of change of speed \(v \)

\begin{equation*} a_\theta = R\left( \frac{d \omega}{dt}\right) = \left( \frac{d R\omega}{dt}\right) = \dfrac{dv}{dt}. \end{equation*}

Example 5.39. Displacement Vector in Cartesian and Polar Coordinates.

A displacement vector is given in the \(xy\)-plane by its magnitude \(2\ \text{m}\) and direction of \(30^{\circ}\) with respect to the \(x\)-axis. Write the displacement vector in terms of the unit vectors (i) \(\{\hat i, \hat j\}\text{,}\) (ii) \(\{ \hat u_r, \hat u_{\theta} \}\) for \(\theta =30^{\circ}\text{,}\) (iii) \(\{ \hat u_r, \hat u_{\theta} \}\) for \(\theta =45^{\circ}\text{,}\) and (iv) \(\{ \hat u_r, \hat u_{\theta} \}\) for \(\theta =90^{\circ}\text{.}\)

Answer.

See solution for answers.

Solution.

Let us denote the three pairs of radial/angular unit vectors in parts (ii), (iii), and (iv) as \((\hat u_r, \hat u_{\theta})\text{,}\) \((\hat u_r^{\prime }, \hat u_{\theta}^{\prime })\text{,}\) \((\hat u_r^{\prime \prime}, \hat u_{\theta}^{\prime \prime})\) respectively. Their expressions in terms of \(\hat i\) and \(\hat j\) are

\begin{align} \hat u_r \amp = \frac{\sqrt{3}}{2} \hat i + \frac{1}{2} \hat j\tag{5.39}\\ \hat u_{\theta} \amp = - \frac{1}{2} \hat i + \frac{\sqrt{3}}{2} \hat j\tag{5.40}\\ \hat u_r^{\prime } \amp = \frac{1}{\sqrt{2}} \hat i + \frac{1}{\sqrt{2}} \hat j\tag{5.41}\\ \hat u_{\theta}^{\prime } \amp = - \frac{1}{\sqrt{2}} \hat i + \frac{1}{\sqrt{2}} \hat j\tag{5.42}\\ \hat u_r^{\prime \prime} \amp= \hat j \tag{5.43}\\ \hat u_{\theta} ^{\prime \prime} \amp= - \hat i \tag{5.44} \end{align}

We can also write \(\hat i\) and \(\hat j\) in terms of these radial/angular unit vector pairs. In general the relation of Cartesian unit vector with the polar unit vectors for a ray in the direction of \(\theta\) will be

\begin{align*} \hat i \amp = \cos\theta\ \hat u_r - \sin\theta\ \hat u_{\theta}\\ \hat j \amp = \sin\theta\ \hat u_r + \cos\theta\ \hat u_{\theta} \end{align*}

Now, we are ready to tackle the problem at hand. The given displacement vector is a radial vector in the direction of \(\theta = 30^{\circ}\text{.}\) Let us denote this vector by \(\vec D\text{.}\)

\begin{align} \vec D \amp = 2\ \text{m}\ \left[ \cos (30^{\circ}) \hat i + \sin (30^{\circ}) \hat j \right]\tag{5.45}\\ \amp = \sqrt{3}\ \text{m}\ \hat i +1\ \text{m}\ \hat j.\tag{5.46} \end{align}

This can be written immediately in terms of \(\hat u_r\text{.}\)

\begin{equation*} \vec D = 2\ \text{m}\ \hat u_r. \end{equation*}

It is also easily written in terms of \(\hat u_r^{\prime \prime}\) and \(\hat u_{\theta} ^{\prime \prime}\) using Eqs. (5.43) and (5.44) in Eq. (5.46).

\begin{equation*} \vec D = \left[ \sqrt{3}\ \text{m}\ (-\hat u_{\theta} ^{\prime \prime}) + 1\ \text{m}\ (\hat u_r^{\prime \prime}) \right]. \end{equation*}

To write this displacement in terms of \(\hat u_r^{\prime }\) and \(\hat u_{\theta}^{\prime }\) we replace \(\hat i\) and \(\hat j\) by

\begin{align*} \amp \hat i = \frac{1}{\sqrt{2}}\ \hat u_r^{\prime } - \frac{1}{\sqrt{2}}\ \hat u_{\theta}^{\prime } \\ \amp \hat j = \frac{1}{\sqrt{2}}\ \hat u_r^{\prime } + \frac{1}{\sqrt{2}}\ \hat u_{\theta}^{\prime } \end{align*}

\begin{align*} \vec D \amp = \left[\sqrt{3}\ \text{m}\ \hat i + 1\ \text{m}\ \hat j \right]\\ \amp = \sqrt{3} \ \text{m}\ \left(\frac{1}{\sqrt{2}}\ \hat u_r^{\prime } - \frac{1}{\sqrt{2}}\ \hat u_{\theta}^{\prime } \right) + 1\ \text{m}\ \left( \frac{1}{\sqrt{2}}\ \hat u_r^{\prime } + \frac{1}{\sqrt{2}}\ \hat u_{\theta}^{\prime } \right)\\ \amp = \frac{\sqrt{3} + 1}{\sqrt{2}} \ \text{m}\ \hat u_r^{\prime } + \frac{\sqrt{3} - 1}{\sqrt{2}} \ \text{m}\ \hat u_{\theta}^{\prime } \end{align*}

Exercises 5.5.4 Exercises

1. Motion of a Person on a Rotating Platform Using Polar Coordinates.

Suppose you are standing on a rotating platform of radius \(5\) meters that is rotating at a constant angular velocity of magnitude \(0.5\) radian per second.

(a) What will be your speed when you are standing at the edge?

(b) What will be your velocity at an instant you are in the direction of \(30^\circ\) with respect to the positive \(x\) axis?

(d) What will be your speed and magnitude of acceleration when you are standing 2 meters from the center.

Hint.

Use definitions.

Answer.

(a) \(2.5\ \text{m/s} \text{,}\) (b) \(2.5\ \text{m/s}\ \hat u_\theta\text{,}\) \(\hat u_\theta-\dfrac{1}{2}\, \hat i+ \dfrac{\sqrt{3}}{2}\, \hat j\text{,}\) (c) \(-1.25\ \text{m/s}\ \hat u_r\text{,}\) \(\hat u_r = \dfrac{\sqrt{3}}{2}\, \hat i+ \dfrac{1}{2}\, \hat j\text{,}\) (d) \(1.0\text{ m/s}\text{,}\) \(0.5\ \text{m/s}^2\text{.}\)

Solution 1. (a) and (b)

Note that parts (a) and (b) are about the circular motion when the radius of the circle is \(R=5\) m and part (c) is for a circular motion in a different radius, viz., \(R=2\text{ m}\text{.}\) Using the formulas for uniform circular motions, we immediately find the following answer.

With \(\omega\) for angular rotation speed and \(v\) for speed, we have

\begin{equation*} v = R\omega = (5\ \text{m}) \times (0.5\ \text{rad/s}) = 2.5\ \text{m/s}. \end{equation*}

(a) Speed, \(\text{.}\) Note that \(\text{m}\ \times\ \text{rad} = \text{m}\text{,}\) since the radian is dimensionless as it is the ratio of arc length to radius, both of dimension length.

(b) For velocity, we also need to specify direction. The direction of velocity is tangent to the circle in the direction of the unit vector \(\hat u_\theta\text{.}\) Therefore, velocity vecor at the instant is

\begin{equation*} \vec v = 2.5\ \text{m/s}\ \hat u_\theta, \end{equation*}

where \(\hat u_\theta\) has the following analytic representation in \(\hat i\) and \(\hat j\text{.}\)

\begin{equation*} \hat u_\theta = -\sin\,\theta\, \hat i+ \cos\,\theta\, \hat j= -\dfrac{1}{2}\, \hat i+ \dfrac{\sqrt{3}}{2}\, \hat j. \end{equation*}

Solution 2. c

Since the motion is uniform circular motion, the direction of acceleration is towards the center, i.e., in the direction of the negative of the unit vector \(\hat u_r\text{.}\) The magnitude is \(a_c\text{,}\)

\begin{equation*} a = \dfrac{v^2}{R} = \dfrac{ (2.5\ \text{m/s})^2 }{5} = 1.25\text{ m/s}^2. \end{equation*}

Therefore, we can write the acceleration vector to be

\begin{equation*} \vec a = -1.25\ \text{m/s}\ \hat u_r, \end{equation*}

where \(\hat u_r\) has the following analytic representation in \(\hat i\) and \(\hat j\text{.}\)

\begin{equation*} \hat u_r = \cos\,\theta\, \hat i+ \cos\,\theta\, \hat j= \dfrac{\sqrt{3}}{2}\, \hat i+ \dfrac{1}{2}\, \hat j. \end{equation*}

Solution 3. d

Similar calculations as those of parts (a) and (b) give the following answer. Speed = \(1.0\) m/s and magnitude of acceleration \(0.5\ \text{m/s}^2\text{.}\) The direction of velocity is pointed in the direction of the unit vector \(\hat u_\theta\) and the direction of the acceleration is pointed towards the center, i.e., in the direction of vector \(-\hat u_r\text{.}\)

2. Particle in Uniform Circular Motion Using Polar Coordinates.

A particle moves in a circle of radius \(R\) with a uniform circular motion of constant angular velocity \(\omega = \omega_0\text{.}\) The particle moves in the \(xy\)-plane in a counter-clockwise manner when observed from the positive \(z\)-axis with the center of the circle of motion at the origin.

At \(t=0\) the particle is at the point whose Cartesian coordinates are \((R,0)\) with respect to origin at the center of the circle of motion. Where will the particle be at an arbitrary time \(T\text{?}\)

Hint.

Constant \(\omega = \omega_0\) means \(\Delta\theta = \omega_0\Delta t\text{.}\)

Answer.

\(\theta(T) = 2\pi \times [\text{fractional part of }(\omega_0 T/2\pi)].\)

Solution.

Since the particle is moving in a circle, it is advantageous to work in polar coordinates. We have the radial coordinate given to be \(r=R\text{,}\) which is independent of time. Therefore, we need to find the angular coordinate at time \(T\text{.}\) Since \(\omega\) is fixed in time, angle at \(t=T\) will be

\begin{equation*} \theta(T) = \omega_0 T. \end{equation*}

Suppose \(\omega_0\) was positive, i.e., a counterclockwise motion. Then, \(\omega_0 T\) can be more than \(2\pi\text{.}\) So, we would need to subtract away angles for full rotations. That is, divide by \(2\pi\) and then collect only the fractional part. Let’s call it \(f\text{.}\)

\begin{equation*} f = \text{fractional part of } (\theta(T)/2\pi). \end{equation*}

Now, we multiply it by \(2\pi\) to get back the angle in radian.

\begin{equation*} \theta = f\times 2\pi\text{ rad}. \end{equation*}

3. (Calculus) Particle in a Non-uniform Circular Motion Using Polar Coordinates.

A particle moves in a circle of radius \(a\) in \(xy\)-plane with a varying angular velocity \(\omega = b t\) counterclockwise, where \(b\) is constant. At \(t=0\) the particle has Cartesian coordinates are \((a,0)\) with respect to the origin at the center of the circle of motion which is at the origin. Where will the particle be at an arbitrary time \(T\text{?}\)

Hint.

Integrate \(d\theta = \omega\, dt\text{.}\)

Answer.

\(r=a,\ \theta= \frac{1}{2}b T^2\text{.}\)

Solution.

Since the particle is moving in a circle, it is advantageous to work in polar coordinates. We have the radial coordinate given to be \(r=a\text{,}\) which is independent of time. Therefore, we need to find the angular coordinate at time \(T\text{.}\) Now, making use of the definition of angular velocity in terms of the derivative of the angular coordinate we find that the angular coordinate changes according to the following equation.

\begin{equation*} \frac{d\theta}{dt} = bt. \end{equation*}

This equation can be solved for general time \(t\text{.}\)

\begin{equation*} \theta(t) = \theta(0) + \frac{1}{2}b t^2. \end{equation*}

The angle at \(t=0\) is zero since the particle was located on the \(x\)-axis. Therefore, the angular coordinate at the desired time is

\begin{equation*} \theta(T) = \frac{1}{2}b T^2. \end{equation*}

We have found that the polar coordinates at the desired time is \((r, \theta) = (a,1/2\ bT^2)\text{.}\) We can convert these into Cartesian coordinates by standard procedure with the result

\begin{align*} \amp x = a \cos \left(\frac{1}{2}bT^2\right).\\ \amp y = a \sin \left(\frac{1}{2}bT^2\right). \end{align*}

4. Motion on a Straight Line Described in Polar Coordinates.

Motion on a straighline is easiest to describe by placing the motion on a Cartesian axis. But, sometimes, we need to work in polar coordinates even for this motion.

In this exercise you will practice getting polar representation of position, velocity and acceleration (vectors) for a particle moving parallel to \(x\) axis at \(y=c\) in the \(xy\)-plane, where \(c\) is some constant. Let \(x=0\) at \(t=0\text{.}\)

Hint.

Better to work using Cartesian unit vectors.

Answer.

See the solution.

Solution.

Let us write position vector in Cartesian component first.

\begin{equation*} \vec r = x\; \hat i + c\; \vec j,\ \ x = r\;\cos\theta. \end{equation*}

In Polar coordinates it will be

\begin{equation*} \vec r = r\; \hat u_r;\ \ r(t=0) = c,\ \ \theta(t=0)=\frac{\pi}{2}. \end{equation*}

Now, the velocity will be

\begin{equation*} \vec v = \frac{d\vec r}{dt} = \frac{dx}{dt}\;\hat i. \end{equation*}

But \(x = r\cos\theta\text{,}\) therefore

\begin{equation*} \frac{dx}{dt} = \frac{dr}{dt}\;\cos\theta - r\;\sin\theta\; \frac{d\theta}{dt} \end{equation*}

For simplicity of notation, let us write \(dr/dt\) as \(v_r\) and \(d\theta/dt\) as \(\omega\text{.}\) Therefore, we have the following for velocity.

\begin{equation*} \vec v = \left( v_r\;\cos\theta - \omega r \; \sin\theta \right)\hat i. \end{equation*}

This is a mix of two different systems. We could remedy this by replacing \(\hat i\) by its expression in \(\hat u_r\) and \(\hat u_\theta\text{.}\) But, that will look complicated. So, I will leave this as it is here.

To get acceleration, we take another derivative. This will give acceleration that will also have only \(x\) components.

\begin{equation*} \vec a = a_x\; \hat i, \end{equation*}

with \(a_x\) as follows (using \(\alpha = d\omega/dt\))

\begin{equation*} a_x = \frac{dv_r}{dt}\;\cos\theta -2\omega v_r\sin\theta - \alpha r \; \sin\theta - \omega^2 r \;\cos\theta . \end{equation*}

5. Motion of a Ball Rolling in a Circular Track.

A ball is rolling in a circular track of radius \(R\) which is in the \(xy\)-plane but the center of the track is not at the origin of the Cartesian coordinate system in use. Instead, the center of the track is at \((x_0,y_0)\text{.}\) The ball has a constant speed of \(v_s\text{.}\) (a) Give an expression of the position vector as a function of time \(\vec r(t)\) in terms of the unit vectors \(\{\hat u_x, \hat u_y\}\) of the Cartesian coordinates. (b) Use your expression for \(\vec r(t)\) to find an expression for the velocity of the particle at an arbitrary time \(t\text{.}\) (c) Use your expression for \(\vec r(t)\) to find an expression of the acceleration of the particle at an arbitrary instant \(t\text{.}\)

Solution 1. a

The circle of motion and the coordinates are shown in the figure.

Supposing that the ball is at the largest positive point at time \(t=0\text{.}\) Then, we can write the \(x\) and \(y\)-coordinates of the ball at an arbitrary time as

\begin{align*} \amp x(t) = x_0 + R \cos(\omega t),\\ \amp y(t) = y_0 + R \sin(\omega t), \end{align*}

where \(\omega = v_s/R\) is the angular speed of the ball.

The position vector \(\vec r(t)\) will be

\begin{equation*} vec r(t) = \left[ x_0 + R \cos(\omega t) \right] \hat u_x + \left[y_0 + R \sin(\omega t)\right] \hat u_y. \end{equation*}

Solution 2. b

Taking the time derivative of \(\vec r\) will give the velocity of the ball.

\begin{equation*} \vec v(t) = \frac{d\vec r}{dt} = \left[ - R\omega \sin(\omega t) \right] \hat u_x + \left[ R\omega \cos(\omega t)\right] \hat u_y. \end{equation*}

Solution 3. c

Taking the time derivative of \(\vec v\) will give the acceleration of the ball.

\begin{equation*} \vec a(t) = \frac{d\vec v}{dt} = - R\omega^2 \left[ \cos(\omega t) \hat u_x + \sin(\omega t) \hat u_y \right]. \end{equation*}

Note that \(\cos(\omega t) \hat u_x + \sin(\omega t) \hat u_y\) is the unit vector pointed from the center of the circle towards the ball. Therefore, if a ball moves uniformly in a circle, the acceleration has the magnitude \(R\omega^2\) and the direction is pointed towards the center of the circle as expected.

6. (Calculus) Practice with a Friend: Motion on a Straight Line Described in Polar Coordinates.

Motion on a straighline is easiest to describe by placing the motion on a Cartesian axis. But, sometimes, we need to work in polar coordinates even for this motion.

In this exercise you will practice getting polar representation of position, velocity and acceleration (vectors) for a particle moving parallel to \(y\) axis at \(x=c\) in the \(xy\)-plane, where \(c\) is some constant. Let \(y=0\) at \(t=0\text{.}\)

7. Practice with a Friend: Elliptical Trajectory In Polar Coordinates.

Planets go around the Sun in elliptical orbits with Sun at one of the foci of the ellipse. A planet’s trajectory is most conveniently written in the polar coordinate. Let \(r,\theta\) be the polar coordinates with origin at the center of the ellipse and \(x\) axis the major axis and \(y\) the minor axis. The ellipse of a planet’s orbit is

\begin{equation*} r = \frac{r_0}{1 - \epsilon\; \cos(\theta)},\ \ r_0 = a(1-\epsilon^2), \end{equation*}

where \(\epsilon\) is eccentricity with values in the range \([0,1)\) and \(a\) is semimajor axis, i.e., \(2a\) is the “diameter” of ellipse on the wide side. Semi-major axis of Mars is \(1.5273\text{ AU}\text{,}\) where \(1\text{ AU} = \) Earth-Sun distance, and the eccentricity of its orbit is \(0.093\text{.}\) (a) Find the Cartesian representation of the orbit of Mars and (b) Find the distances when Mars gets (i) closest to the Sun (perihelion) and (ii) farthest from the Sun (aphelion .

Answer.

(b) (i) \(1.38\text{ AU}\text{,}\) \(1.666\text{ AU}\text{.}\)

8. (Calculus) Practice with a Friend: Spiral Trajectory with Zero Radial Acceleration.

Consider a motion described by the following velocities of polar coordinates of a particle.

\begin{align*} \amp \frac{d\theta}{dt} = \omega,\ \text{constant} \\ \amp \frac{dr}{dt} = \omega\; r \end{align*}

(a) Prove that radial component of acceleration, \(a_r = 0\text{.}\) (b) Let \(r=r_0\) and \(\theta=0\) at \(t=0\text{,}\) show that \(r(t) = r_0 e^{\omega t}\text{.}\) (c) A small element of the trajectory can be given by \(r d\theta\) by using the arc-angle formula. Use this to find the total distance on the spiral traveled in time \(T\text{.}\) (d) Find \(x(t)\) and \(y(t)\) and plot the trajectory (i.e., \(y\) versus \(x\)) for \(\omega=0.1,\ r_0=1.0\) from \(0 \le t \le 20\text{.}\)

Answer.

Prev Top Next