I will work out the numerical problem.
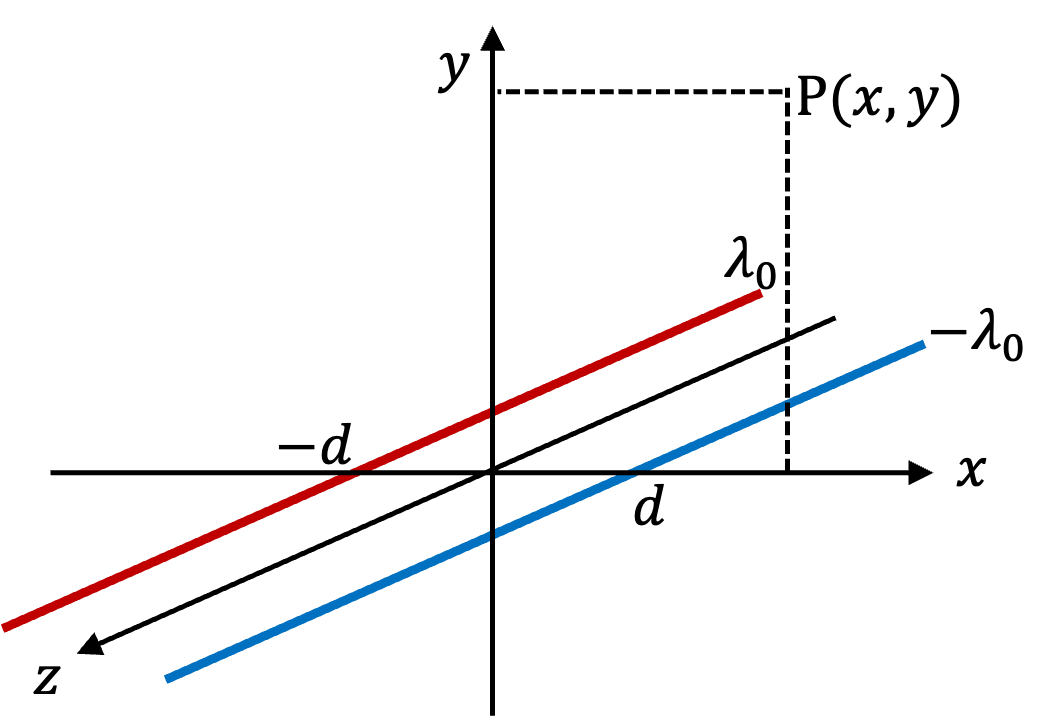
Let \(r_1\) and \(r_2\) be the distance from the wires to the field point \((x,y)\) in the \(xy\)-plane .
\begin{align*}
r_1 \amp = \sqrt{(x+d)^2 + y^2}, \\
\amp = \sqrt{(2+1)^2 + 4^2} = 5\text{ cm}, \\
r_2 \amp = \sqrt{(x-d)^2 + y^2}, \\
\amp = \sqrt{(2-1)^2 + 4^2} = \sqrt{17}\text{ cm}.
\end{align*}
Using the formulas for the magnitudes of the electric fields from charges on long wire, which is done by Gauss’s law for cyclindrical case, we get
\begin{align*}
E_1 \amp = \dfrac{|\lambda_1|}{2\pi\epsilon_0}\,\dfrac{1}{r_1} \\
\amp = \dfrac{ 10\times 10^{-6}}{2\pi\times8.85\times 10^{-12}}\,\dfrac{1}{5} = 35,967\text{ N/C} \\
E_2 \amp = \dfrac{|\lambda_2|}{2\pi\epsilon_0}\,\dfrac{1}{r_2} \\
\amp = \dfrac{ 10\times 10^{-6}}{2\pi\times8.85\times 10^{-12}}\,\dfrac{1}{\sqrt{17}} = 67,972\text{ N/C}
\end{align*}
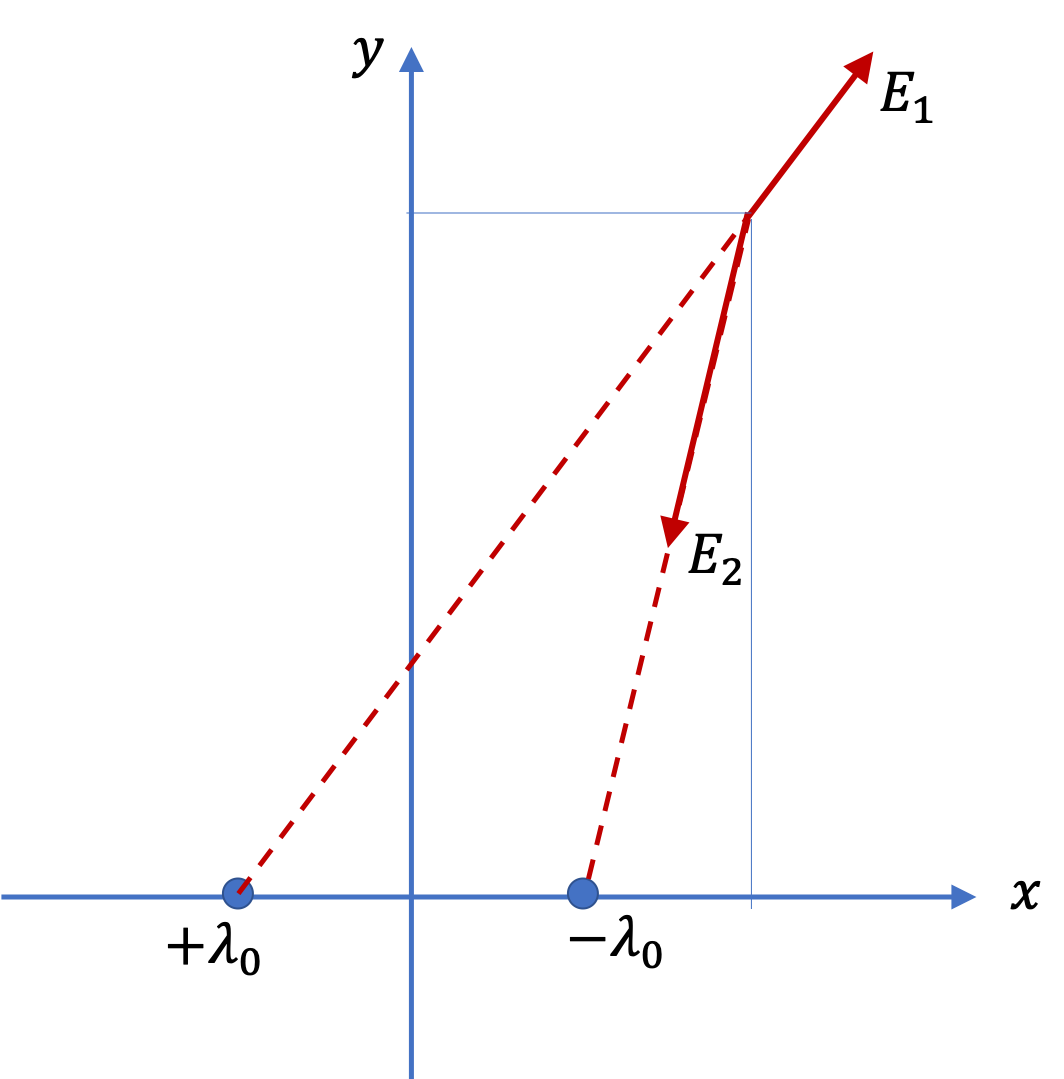
Now we need to add them vectorially. The net field is not just sum of the magnitudes, as you know from vector addition.
\begin{equation*}
E_P \ne E_1 + E_2.
\end{equation*}
We will first compute \(x\) and \(y\) components of the two fields so that we can find \(x\) and \(y\) components of the net field.
\begin{align*}
E_{1x} \amp = E_1\, \dfrac{x+d}{r_1}, \\
\amp = 35,967\text{ N/C}\, \dfrac{3}{5} = 21,580\text{ N/C}, \\
E_{1y} \amp = E_1\, \dfrac{y}{r_1}, \\
\amp = 35,967\text{ N/C}\, \dfrac{4}{5} = 28,774\text{ N/C}.
\end{align*}
Similarly, we work out the components of the field of wire 2. But, here we need to multiply by \(-1\) since we have a negative charge.
\begin{align*}
E_{2x} \amp = E_2\, \dfrac{-(x-d)}{r_2}, \\
\amp = 67,972\text{ N/C}\, \dfrac{-1}{\sqrt{17}} = -16,486\text{ N/C}, \\
E_{2y} \amp = E_2\, \dfrac{-y}{r_2}, \\
\amp = 67,972\text{ N/C}\, \dfrac{-4}{\sqrt{17}} = -65,943\text{ N/C}.
\end{align*}
Therefore, the components of the net field are
\begin{align*}
E_x \amp = E_{1x} + E_{2x} = 21,580 -16,486 = 5,094\text{ N/C},\\
E_y \amp = E_{1y} + E_{2y} = 28,774 - 65,943 = -37,169\text{ N/C}
\end{align*}