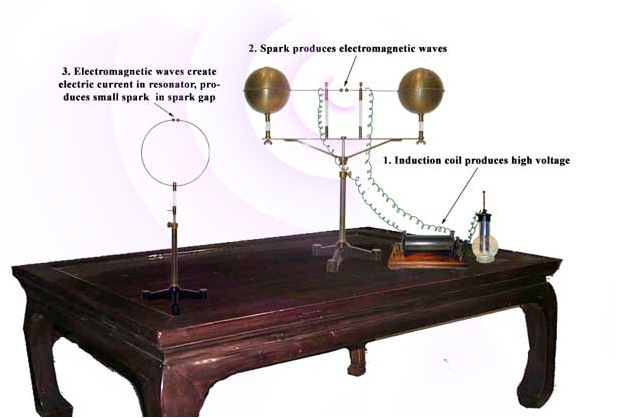
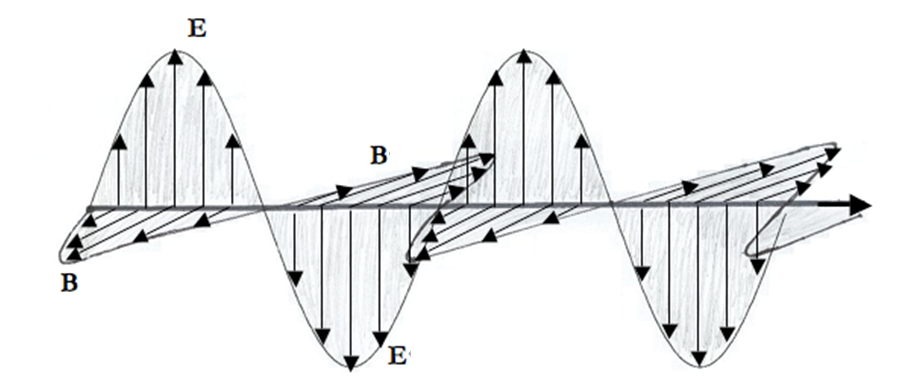
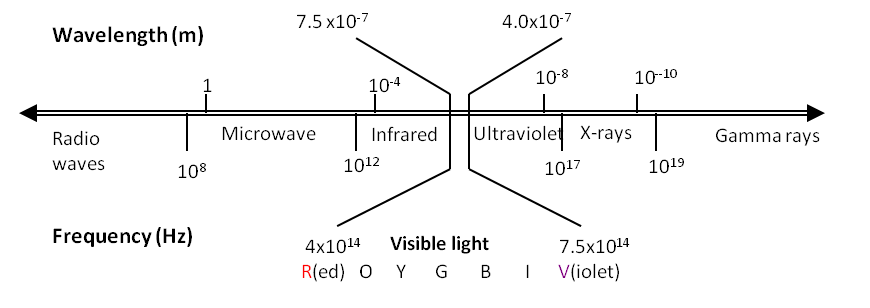
For simplicity we seek EM waves moving in the \(x\) direction and electric and magnetic fields that are independent of \(y\) and \(z\text{.}\) We make a further simplification: let the electric field have only the \(y\)-component everywhere. These choices leave only \(E_y\) and \(\vec B\) to be determined and their dependences are reduced to only two variables \(x\) and \(t\text{.}\)
\begin{equation*}
\text{Unknowns:}\ \ E_y(x,t)\ \ \text{and}\ \ \vec B(x,t).
\end{equation*}
Writing out the first Maxwell’s equation, Eq.
(42.11) for the empty space explicitly in the Cartesian coordinates we find that it is automatically satisfied by the assumed component and functional dependence of electric field.
\begin{equation*}
\vec{\nabla}\cdot\vec E = \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} + \frac{\partial E_z}{\partial z} = 0.
\end{equation*}
We now look at the components of the third Maxwell’s equation, the Faraday law given in Eq.
(42.13), keeping only the non-zero terms.
\begin{align*}
\amp x\text{-component:}\ \ \frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z} = -\frac{\partial B_x}{\partial t} \Longrightarrow \frac{\partial B_x}{\partial t} =0\\
\amp y\text{-component:}\ \ \frac{\partial E_x}{\partial z} - \frac{\partial E_z}{\partial x} = -\frac{\partial B_y}{\partial t} \Longrightarrow \frac{\partial B_y}{\partial t} =0\\
\amp z\text{-component:}\ \ \frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y} = -\frac{\partial B_z}{\partial t} \Longrightarrow \frac{\partial E_y}{\partial x} = -\frac{\partial B_z}{\partial t}
\end{align*}
Since the \(x\)- and \(y\)-components of \(\vec B\) are independent of time, they will not be in the wave solution. Therefore, we will set them to zero.
\begin{equation*}
B_x = 0;\ \ \ B_y = 0.
\end{equation*}
This leaves only \(E_y\) and \(B_z\) non-zero.
\begin{equation*}
\text{Unknowns left:}\ \ E_y(x,t)\ \ \text{and}\ \ B_z(x,t).
\end{equation*}
Finally, we work out the components of the Ampere-Maxwell’s law when \(\vec E\) and \(\vec B\) are independent of \(y\) and \(z\text{.}\)
\begin{align*}
\amp x\text{-component:}\ \ \frac{\partial B_z}{\partial y} - \frac{\partial B_y}{\partial z} = \mu_0 \epsilon_0 \frac{\partial E_x}{\partial t} \Longrightarrow 0 =0\nonumber\\
\amp y\text{-component:}\ \ \frac{\partial B_x}{\partial z} - \frac{\partial B_z}{\partial x} = \mu_0 \epsilon_0\frac{\partial E_y}{\partial t} \Longrightarrow \frac{\partial B_z}{\partial x} = - \mu_0 \epsilon_0\frac{\partial E_y}{\partial t}\\
\amp z\text{-component:}\ \ \frac{\partial B_y}{\partial x} - \frac{\partial B_x}{\partial y} = \mu_0 \epsilon_0\ \frac{\partial E_z}{\partial t} \Longrightarrow 0 = 0
\end{align*}
where I have written \(0 = 0\) for the equations that are automatically satisfied. These calculations show that \(E_y\) and \(B_z\) are not independent. They are related by
\begin{align}
\amp \frac{\partial E_y}{\partial x} = -\frac{\partial B_z}{\partial t} \tag{42.15}\\
\amp \frac{\partial B_z}{\partial x} = - \mu_0 \epsilon_0\frac{\partial E_y}{\partial t} \tag{42.16}
\end{align}
These two equations show that you do not have to solve for both \(E_y\) and \(B_z\text{.}\) If you know one, you can get the other. Therefore, the number of unknowns now becomes one.
\begin{equation*}
\text{Unknowns: either}\ E_y \text{ or }\ B_z.
\end{equation*}
We can eliminate
\(E_y\) or
\(B_z\) from Eqs.
(42.15) and
(42.16) to obtain separate equations for
\(E_y\) and
\(B_z\text{,}\) only one of which we need to solve.
\begin{align}
\amp \frac{\partial^2 E_y}{\partial x^2} = \mu_0\epsilon_0 \frac{\partial^2 E_y}{\partial t^2}\tag{42.17}\\
\amp \frac{\partial^2 B_z}{\partial x^2} = \mu_0\epsilon_0 \frac{\partial^2 B_z}{\partial t^2} \tag{42.18}
\end{align}
Suppose we choose to solve for
\(E_y\text{.}\) A simple solution of Eq.
(42.17) is a traveling wave along the
\(x\)-axis with a speed
\(v\text{.}\)
\begin{equation}
E_y(x,t) = E_0\cos\left[ k(x \pm vt) \right]. \tag{42.19}
\end{equation}
Here the minus sign corresponds to a wave moving in the direction of the positive
\(x\)-axis and the plus sign to the wave moving towards the negative
\(x\)-axis. This solution must satisfy Eq.
(42.17). Plugging into Eq.
(42.17) we immediately find that the speed of the wave has a particular value.
\begin{equation*}
v = \frac{1}{\sqrt{\mu_0\epsilon_0}}.
\end{equation*}
From the known values of \(\mu_0\) and \(\epsilon_0\) we find that the speed \(v\) has the following value:
\begin{equation*}
v = \frac{1}{\sqrt{\mu_0\epsilon_0}} = 3\times 10^8\: \text{m/s} = c,
\end{equation*}
which is equal to the speed of light in vacuum! The speed of light in vacuum is also denoted by the small letter \(c\text{.}\) Hence, the electric field wave travels at the speed of light. A similar argument for the magnetic field gives the same conclusion for the magnetic field wave. Hence, Maxwell’s equations in vacuum naturally predict that the waves of electric and magnetic fields travel at the speed of light.
When writing the solution in the form given in Eq.
(42.19) I have assumed that the electric field at the origin at
\(t=0\) has an amplitude
\(E_0\text{.}\) To allow for other possibilities for the value at the origin at
\(t=0\) you can include a phase constant
\(\phi\) in the argument of the cosine.
\begin{equation}
E_y(x,t) = E_0\cos\left[ k(x \pm vt) +\phi\right]. \tag{42.20}
\end{equation}
For simplicity let us drop \(\phi\) and consider only the waves moving towards the positive \(x\)-axis. That is, we now look at \(E_y\) given by the following
\begin{equation}
E_y(x,t) = E_0\cos\left[ k(x - vt)\right]. \tag{42.21}
\end{equation}
What is the associated magnetic field wave? If the solution of
\(E_y\) has this form, then, from Eqs.
(42.15) and
(42.16), the magnetic field component
\(B_z\) must obey
\begin{align}
\amp \frac{\partial B_z}{\partial t} =- k E_0\sin\left[ k(x - vt)\right] \tag{42.22}\\
\amp \frac{\partial B_z}{\partial x} = \mu_0 \epsilon_0\; k \; v \sin\left[ k(x - vt)\right]\tag{42.23}
\end{align}
These two equations say that \(B_z\) has the same form as \(E_y\)
\begin{equation*}
B_z(x,t) = B_0\cos\left[ k(x - vt) \right],
\end{equation*}
with the amplitude \(B_0\) given by
\begin{equation*}
B_0 = \frac{E_0}{v}.
\end{equation*}
Thus, we arrive at the solution of the Maxwell’s equations that corresponds to an electromagnetic wave traveling towards the positive \(x\)-axis. There are two waves, one for \(E_y\) and the other for \(B_z\) that travel at speed \(v=1/\sqrt{\mu_0\epsilon_0}\) and are described by the following functions.
\begin{align}
\amp E_y(x,t) = E_0\cos\left[ k(x - vt) \right]\tag{42.24}\\
\amp B_z(x,t) = \frac{E_0}{v}\cos\left[ k(x - vt) \right]\tag{42.25}
\end{align}