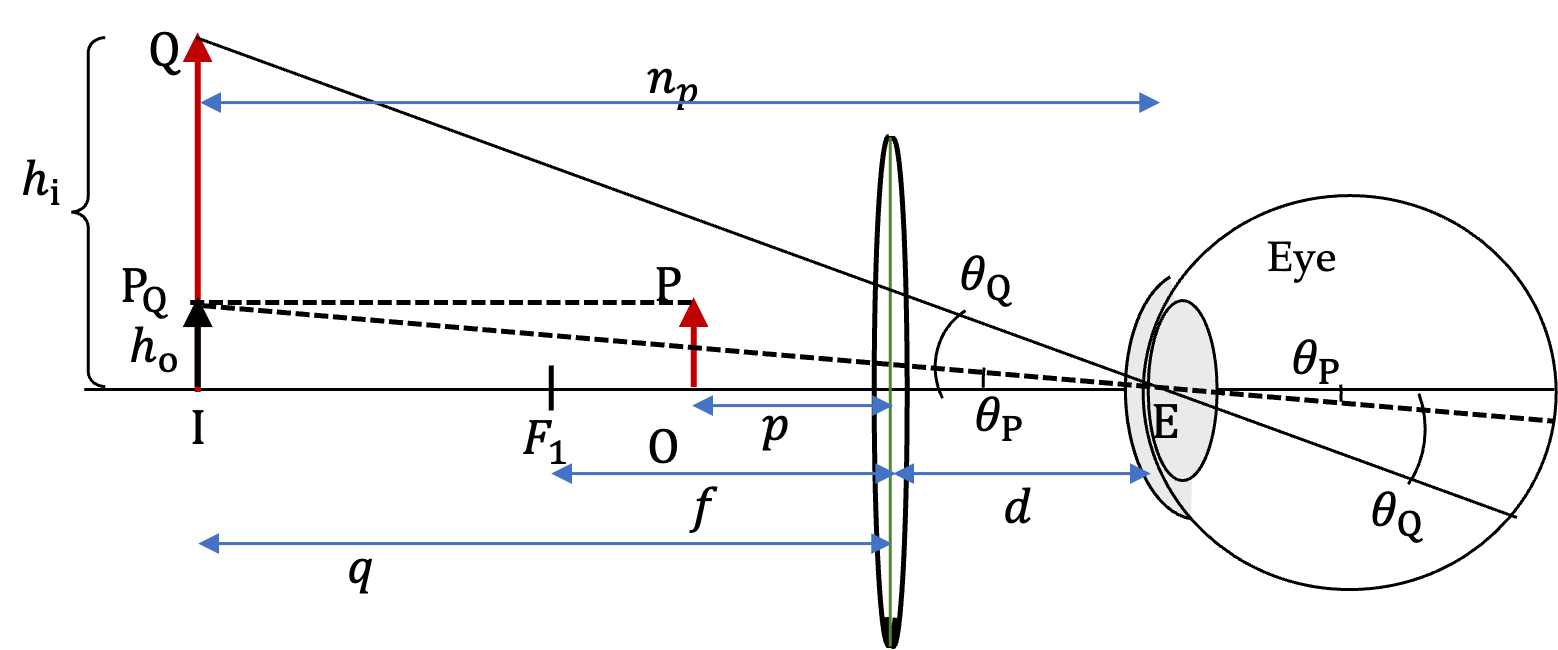
We can work out the angular magnification by exploiting the geometry in
Figure 45.14. Since both the virtual image and the
virtually moved object are at the near point of the eye, we get the following for the angles subtended at the eye.
\begin{align*}
\amp \tan\theta_\text{P} = \frac{h_\text{o}}{n_p} \\
\amp \tan\theta_\text{Q} = \frac{h_\text{i}}{n_p} = \frac{h_\text{i}}{n_p}
\end{align*}
If we make small angle approximation, then, we will have
\begin{align*}
\amp \theta_\text{P} \approx \frac{h_\text{o}}{n_p} \\
\amp \theta_\text{Q} \approx \frac{h_\text{i}}{n_p}
\end{align*}
Therefore, the angular magnification will be
\begin{equation*}
M = \frac{\theta_\text{Q}}{\theta_\text{P}} = \frac{h_\text{i}}{h_\text{o}}.
\end{equation*}
That is, the angular magnification in the small angle approximation is numerically equal to the the lateral magnification of the magnifying glass itself. We can replace \(h_\text{i}/h_\text{o}\) by \(-q/p\) by the magnifying glass itself.
\begin{equation*}
\frac{h_\text{i}}{h_\text{o}} = -\frac{q}{p} = \frac{n_p+f}{f}.
\end{equation*}
Therefore, the angular magnification can also be written as
\begin{equation}
M = \frac{n_p+f}{f} = 1 + \frac{n_p}{f}.\tag{45.11}
\end{equation}
This says that farther the near point larger the angular magnification you will perceive for the same magnifying glass. So, if your friend says he sees the magnification only \(5\times\) with a magnifier that has focal length \(4.5\text{ cm}\) and you say you see magnification \(7\times\text{.}\) Both of you may be right; the different perceptions can be due to different \(n_p\) values: for instace, your \(n_p \approx 31.5\text{ cm}\) and your friend’s \(n_p \approx 22.5\text{ cm}\text{.}\)
Using a standard value of \(25\,\text{cm}\) for \(n_p\) angular magnification is usually written as
\begin{equation}
M = 1 + \frac{25\,\text{cm}}{f}.\tag{45.12}
\end{equation}