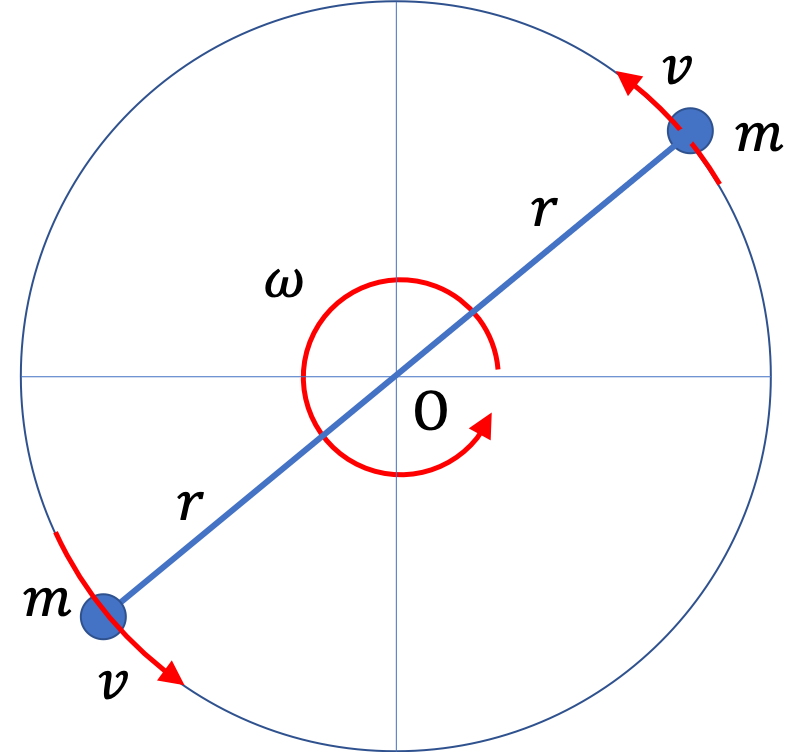
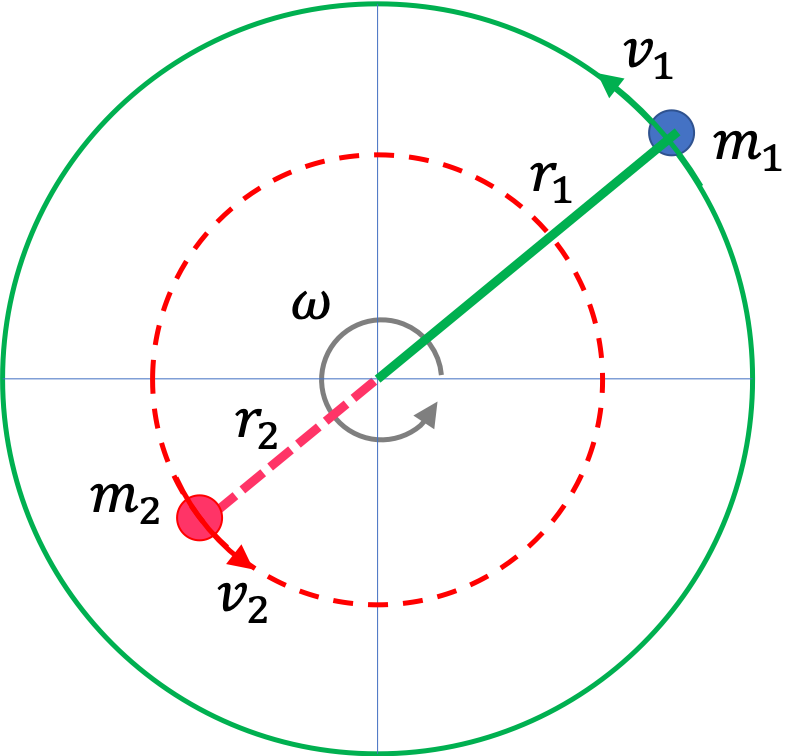
To do that let us examine rotational work done over an interval. The work by all torques on a system will be obtained by summing \(\mathcal{T} \Delta\theta\) from the initial time to the final time for each torque.
\begin{equation}
W_{if}^{\text{rot}} = \sum\, \mathcal{T} \Delta\theta.\tag{9.92}
\end{equation}
Now, recall that \(\alpha\) in \(\mathcal{T}=I\alpha\) is actually \(\Delta\omega/\Delta t\) for infinitesimal \(\Delta t\text{,}\) i.e., rate of change of angular velocity. Therefore, we write
\begin{equation}
{\mathcal{T}}_{\text{net}} = I \, \alpha = I \, \dfrac{\Delta \omega}{\Delta t}.\tag{9.93}
\end{equation}
Using this
\(\mathcal{T}\) in Eq.
(9.92) we get
\begin{equation*}
W_{if}^{\text{rot}} = \sum\, I \, \dfrac{\Delta \omega}{\Delta t} \Delta\theta = \sum\, I \,\Delta \omega\, \dfrac{\Delta\theta}{\Delta t}= \sum\, I \,\Delta \omega\, \omega.
\end{equation*}
(Calculus Step) The right hand side is a cumulative effect of infinitesimal intervals, which makes it an integral.
\begin{equation*}
W_{if}^{\text{rot}} = \int_{\omega_i}^{\omega_f} I \, \omega\, d\omega.
\end{equation*}
Carrying out the integral we get
\begin{equation}
W_{if}^{\text{rot}} = \dfrac{1}{2}\, I\omega_f^2 - \dfrac{1}{2}\, I\omega_i^2.\tag{9.94}
\end{equation}
The quantity \(\dfrac{1}{2} I\omega^2\) is rotational kinetic energy of the body. We will denote this by \(K_{\text{rot}}\text{.}\)
\begin{equation}
K_{\text{rot}} = \dfrac{1}{2} I\omega^2.\tag{9.95}
\end{equation}
Writing Eq.
(9.94) in the following form gives us the result the net rotational work is the change in rotational kinetic energy.
\begin{equation}
W_{if}^{\text{rot}} = K_{f}^{\text{rot}} - K_{i}^{\text{rot}}.\tag{9.96}
\end{equation}