Adding Vectors

Section 3.3 Adding Vectors

Vectors are not like simple numbers. They have magnitude, which is a simple positive number, but they also have a direction, which is not a number but a description. Addition of vectors requires special procedure and much care.

There are basically two ways to add vectors - (1) graphically, and (2) analytically. The graphical addition procedure is more visual and important for understanding how vectors act together to produce a net vector. The analytical procedure is algebraic and hides much of the intuition, but it is also much easier to implement, especially when multiple vectors have to be added.

Subsection 3.3.1 Adding Vectors Graphically

We have already done this in the section on using arrows with a scale for the length-to-magnitude relation to represent vectors. The main idea is in the parallelogram law of addition of vectors. You can review that section and then come back here to get other ways of adding vectors.

For the sake of review, let us use our intuition by looking at adding two force vectors. Suppose two of your friends push on you at right angles to each other. You know that the net effect will be at an angle between them. Another thing that you might not notice in this simple experiment is that the net force on you will be less than the sum of the two forces. For instance, one friend pushed on you with \(10\text{ N}\) and the other friend with \(15\text{ N}\text{,}\) then net force on you will NOT BE \(25\text{ N}\) if they are pushing at right angle to each other.

It has been known for a long time that forces add such that if you draw forces on the two sides of a parallelogram, their sum will have magnitude and direction of one of the diagnals of the parallelogram. Which diagonal? Well, if you draw both force coming out of a common vertex with the same scale as in Figure 3.73, then, net force will be along the diagonal with that same vertex. This is called parallelogram law of addition. Not only forces, but all vectors add this way.

An alternative view of vector addition by a diagram is shown in Figure 3.74(b) with position vectors \(\vec r_1\) and \(\vec r_2\text{.}\) Here, we move the second vector so that it starts at the tip of the first vector. Then, the vector from the tail of the first vector to the tip of the second vector would be the same as the diagonal of the corresponding parallelogram, and hence would be the sum of the two vectors. This method is often called tip-to-tail method of addition.

Figure 3.74. Illustrating vector sum, \(\vec r_{\text{sum}} = \vec r_1 + \vec r_2\text{.}\) (a) The Parallelogram View: Form a paralleogram from \(\vec r_1\) and \(\vec r_2\text{,}\) then the diagonal will be the sum \(\vec r_{\text{sum}}\text{.}\) (b) The Triangle View: Place the tail of vector \(\vec r_2\) at the tip of vector \(\vec r_1\text{,}\) then the sum is the vector from the tail of \(\vec r_1\) to the tip of \(\vec r_2\text{.}\)

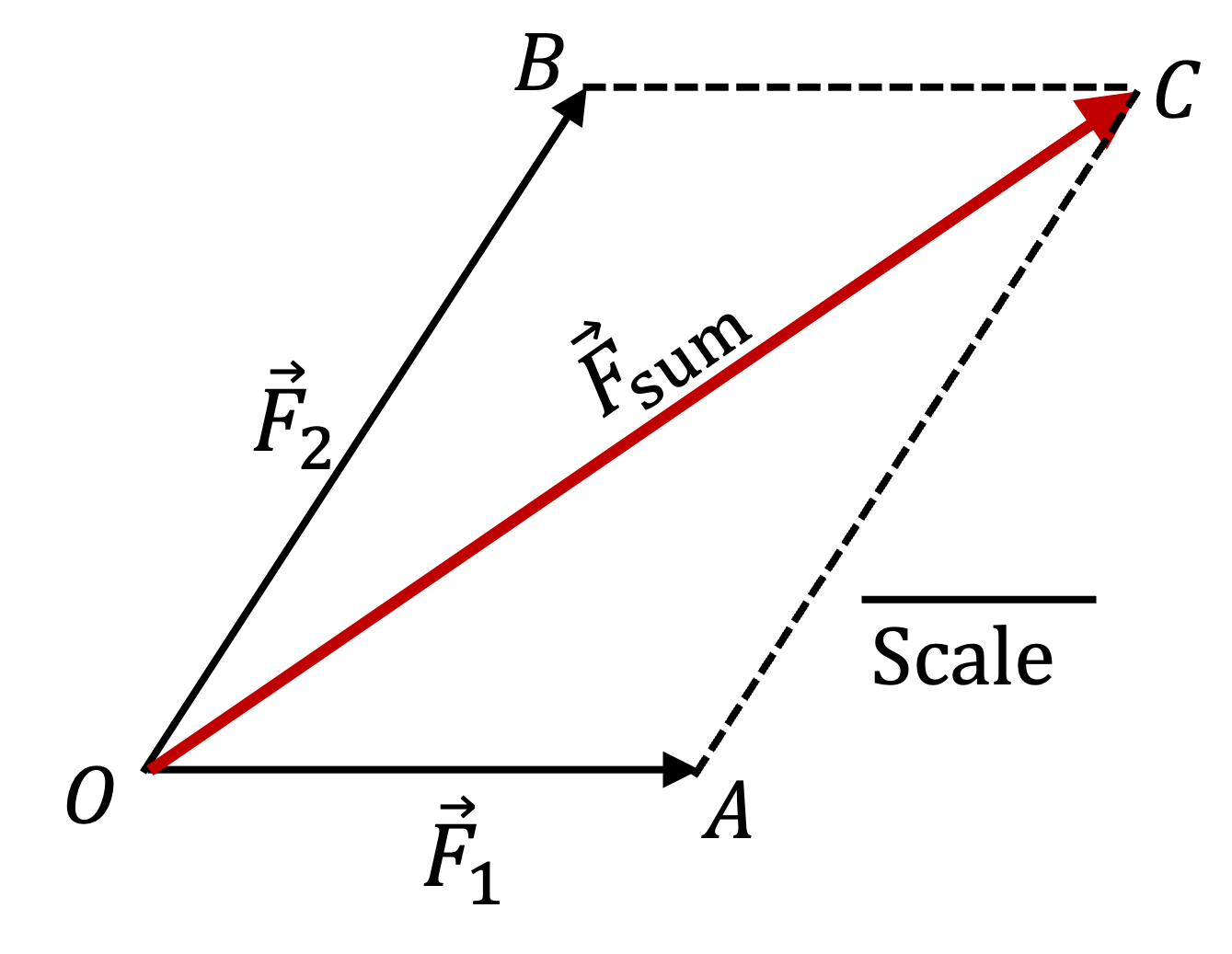
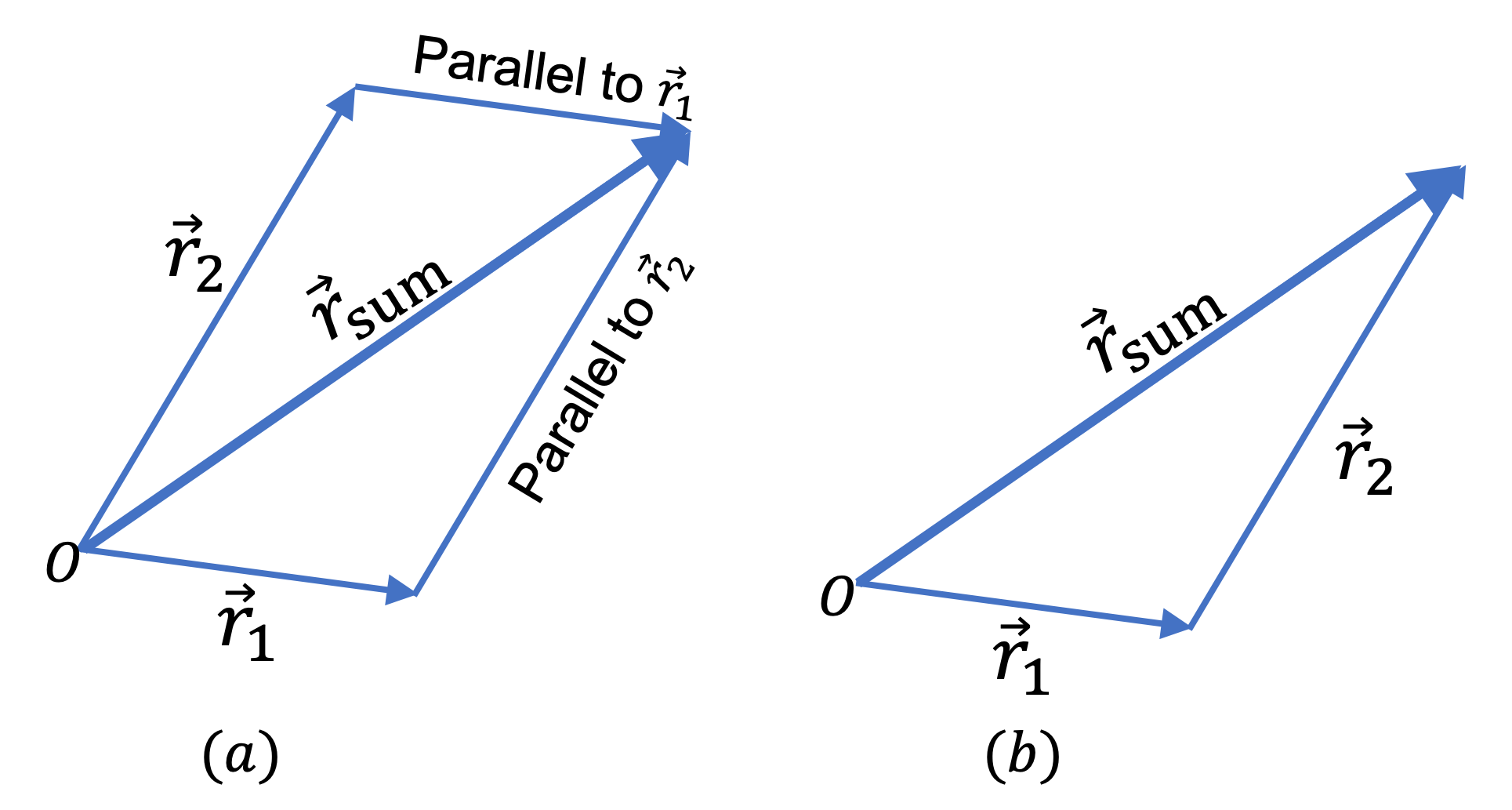
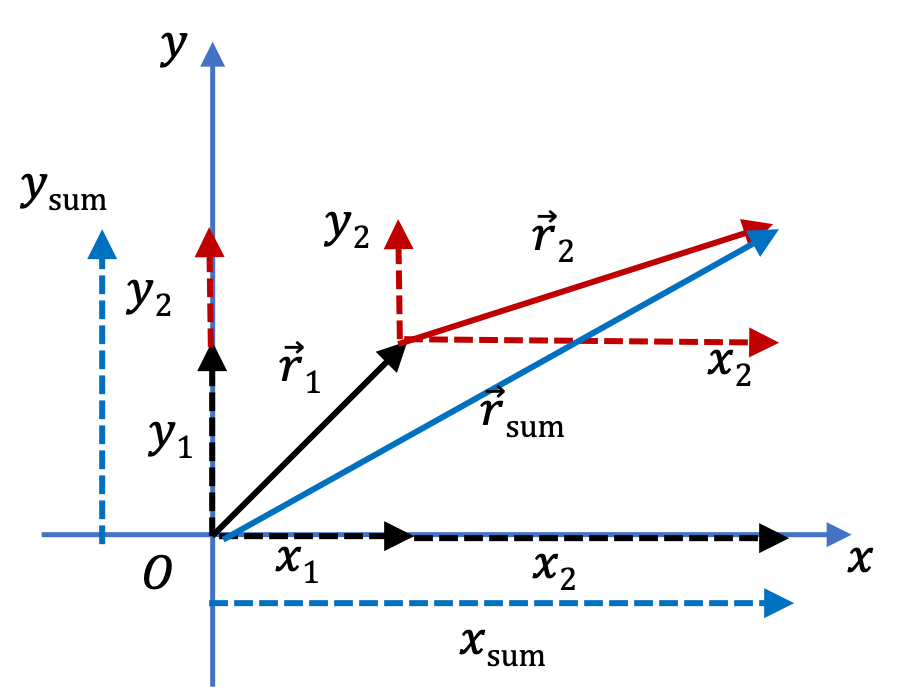
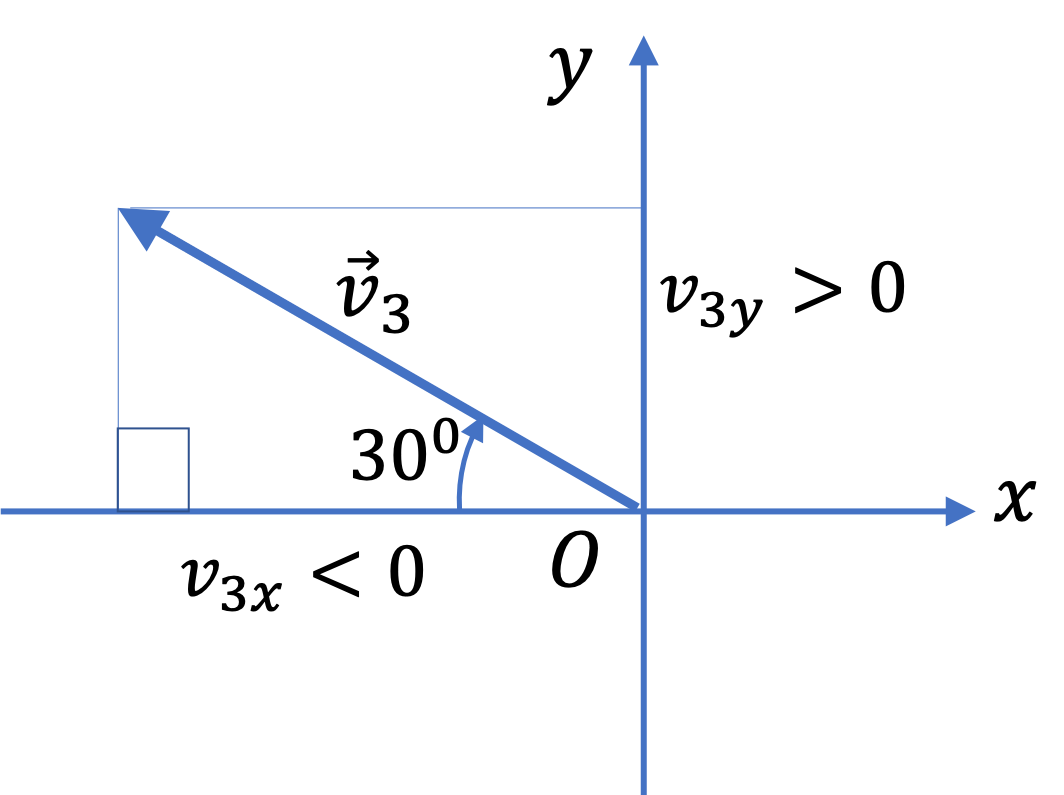
Example 3.75. Adding Vectors Graphically.

(a) From Figure 3.76 , read off magnitudes and directions of vectors \(\vec A \) and \(\vec B \text{,}\) draw the negative of vector \(\vec B \text{.}\) Lets call it \(\vec C\text{.}\)

(b) Find the magnitude and direction of \(\vec A - \vec B\) in two ways: (i) from the components of \(\vec A + \vec C\text{,}\) and (ii) graphically from the parallelogram formed by \(\vec A \) and \(\vec C \text{.}\)

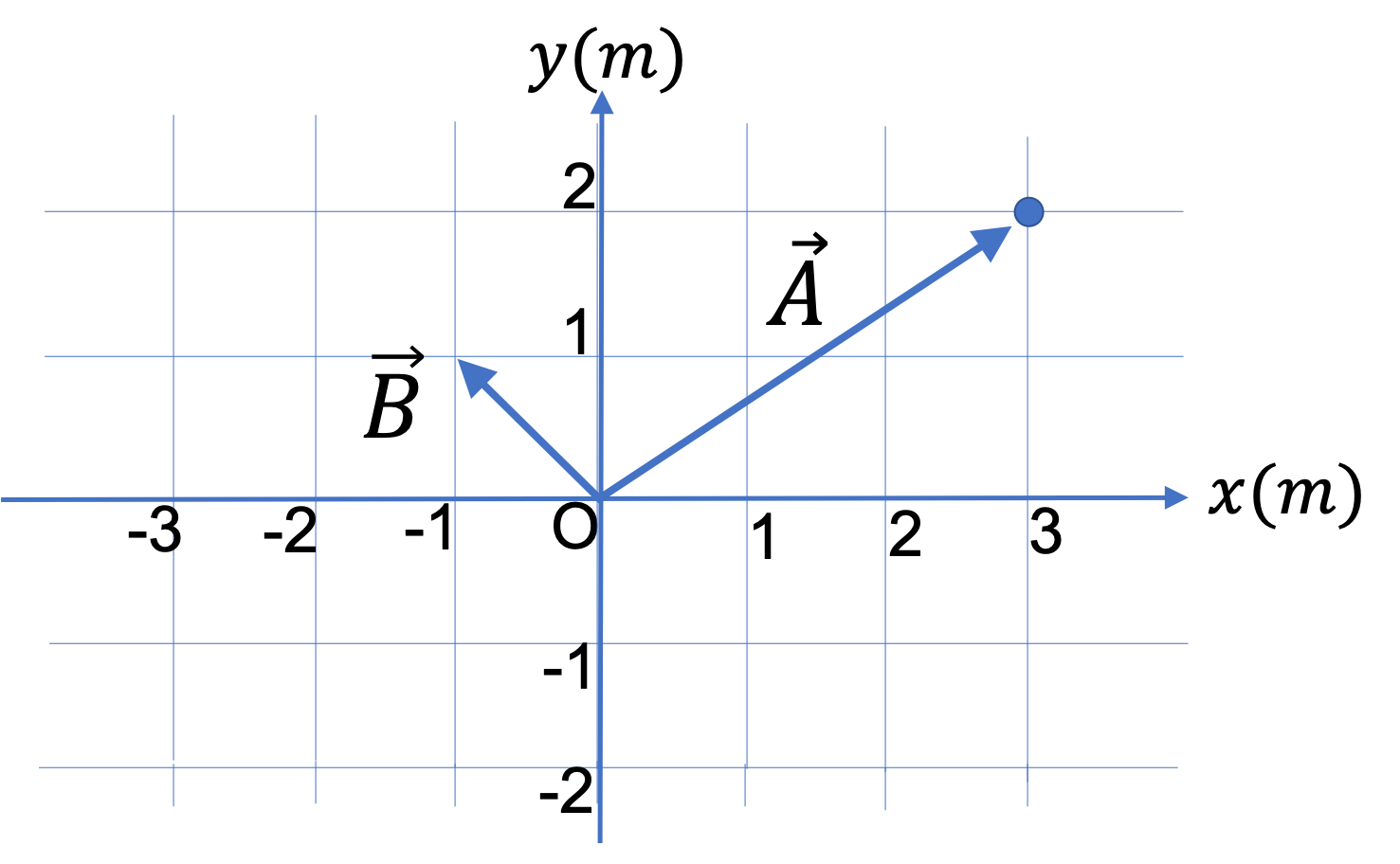
Answer.

(b) (i) \(\sqrt{17}\text{ m}, 14.0^{\circ} \) counterclockwise from \(+x\) axis.

Solution 1. a

We first draw vector \(\vec C\) as shown in Figure 3.77.

Figure 3.77. Figure for Example 3.75(a).

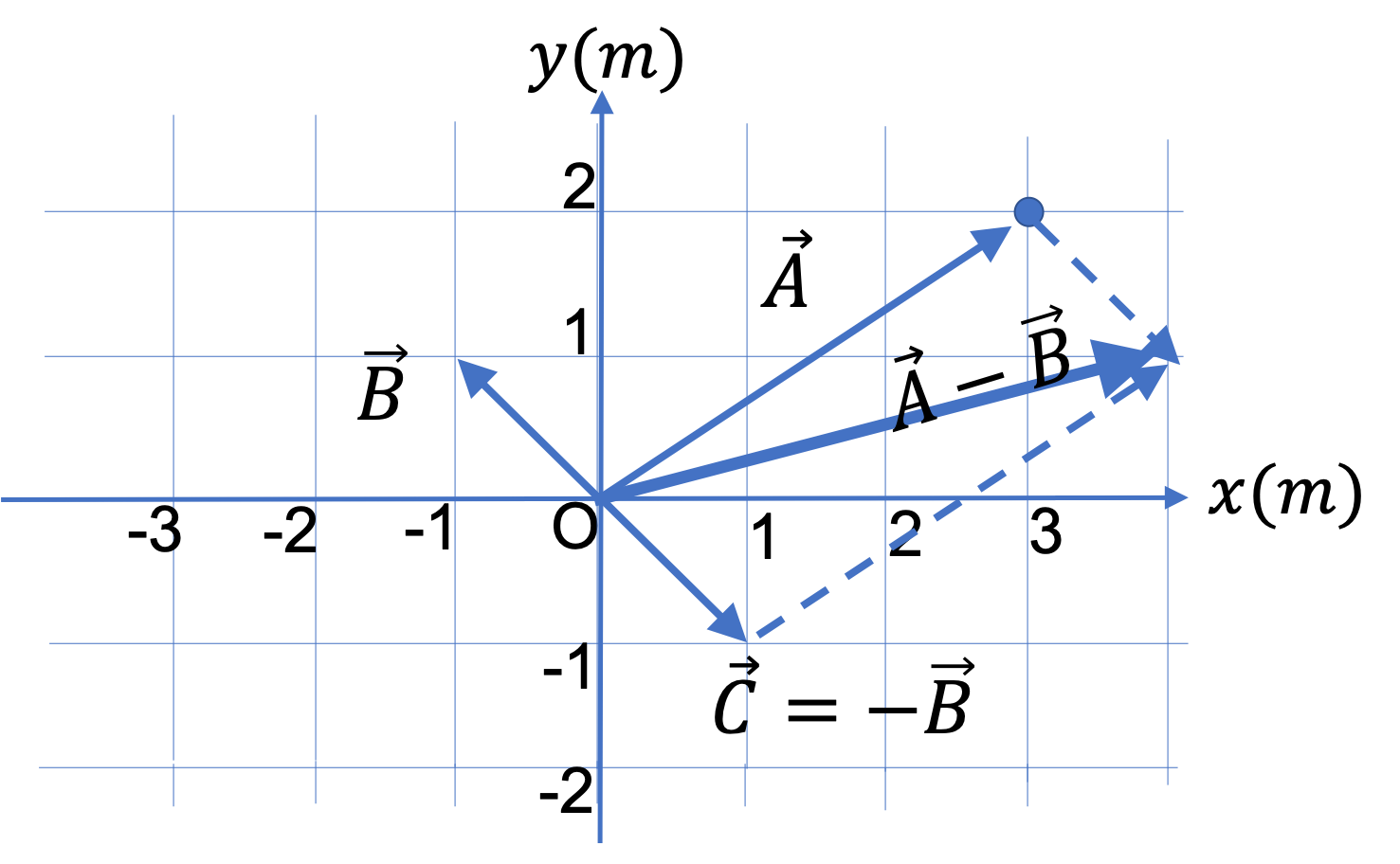
Solution 2. b

(i) We add \(\vec A \) and \(\vec C\) using their components. Let’s denote the sum by \(\vec D\text{.}\)

\begin{align*} \amp D_x = A_x + C_x = 3 + 1 = 4.\\ \amp D_y = A_y + C_y = 2 - 1 = 1. \end{align*}

Therefore, the magnitude and angle are:

\begin{align*} \amp D = \sqrt{D_x^2 + D_y^2 } = \sqrt{17}\text{ m}.\\ \amp \theta = \tan^{-1}\left( \dfrac{1}{4}\right) = 14.0^{\circ}. \end{align*}

Since \((4,1) \) is in the first quadrant, the direction is this angle counterclockwise from the positive \(x \) axis.

(ii) I printed out the figure and used a ruler and a protractor to get the length and the angle - this will give only approximate values, and that’s okay. Read directly, the magnitude is \(\approx 4.0 \) and the counterc;ockwise angle from the positive \(x \) axis is \(\approx 15^{\circ}\text{.}\) These values are close enough to the exact values in (i).

Subsection 3.3.2 Adding Vectors Analytically Component-by-Component

The diagramatic addition of vectors illustrated above is very visual and is good for building intuitions and for appreciating the fact that VECTORS DO NOT ADD LIKE REGULAR NUMBERS. There is an alternative approach based on first converting given vectors into sum of vectors along Cartesian axes (or any orthogonal set of axes, for that matter). This method is called the Analytic Method.

Suppose you have two position vectors \(\vec r_1 \) and \(\vec r_2 \) and you want their sum \(\vec r_{\text{sum}} \) as shown in Figure 3.78. Formally, we write the parallelogram addition of vectors \(\vec r_1 \) and \(\vec r_2 \) as a vector equation.

\begin{equation} \vec r_{\text{sum}} = \vec r_1 + \vec r_2.\tag{3.10} \end{equation}

Beware: THIS DOES NOT MEAN THAT THE LENGTH OF THE SUM VECTOR IS EQUAL TO THE SUM OF THE LENGTHS OF THE TWO VECTORS BEING SUMMED!!!.

\begin{equation*} \text{length of }\vec r_{\text{sum}} \ne (\text{length of }\vec r_{1}) + (\text{length of }\vec r_{2}). \end{equation*}

Replacing Eq. (3.10) by coordinate representations of the three vectors, we might write it like the following.

\begin{equation*} x_{\text{sum}}\,\hat u_x + y_{\text{sum}}\,\hat u_x = x_1\,\hat u_x + y_1\,\hat u_x + x_2\,\hat u_x + y_2\,\hat u_x. \end{equation*}

Or, in a more compact notation, in which we suppress writing the unit vectors explicitly.

\begin{equation*} \left( x_{\text{sum}}, y_{\text{sum}}\right) = (x_1, y_1) + (x_2, y_2). \end{equation*}

If you look at the diagram in (b), you will immediately see that \(x_\text{sum}\) is just sum of \(x_1\) and \(x_2\text{,}\) and similarly for the \(y\) parts.

\begin{align} \amp x_{\text{sum}} = x_1 + x_2,\tag{3.11}\\ \amp y_{\text{sum}} = y_1 + y_2.\tag{3.12} \end{align}

Figure 3.78. Analytical addition of two vectors.

Now, if we wanted the magnitude and direction of the sum vector, we can just use the \((x,y) \) to \((r, \theta)\) transformations, as we do for any vector.

\begin{align} \amp r_{\text{sum}} = \sqrt{ x_{\text{sum}}^2 + y_{\text{sum}}^2 }\tag{3.13}\\ \amp \tan \theta_{\text{sum}} = \dfrac{ y_{\text{sum}} }{ x_{\text{sum}} } \tag{3.14} \end{align}

Once we get the angle, we deduce the direction from the angle value based on the quadrant the vector is pointed, and then we state the direction as clockwise or counterclockwise angles from Cartesian axes.

Often a table of components helps organize the calculations. This is illustrated in Exercise 3.3.3.2.

Example 3.79. Adding Two Forces Given in Component Form.

Suppose a box is being pushed by two forces, which are given to us in component form, as \((F_x, F_y)\text{:}\)

\begin{equation*} \vec F_1 = (20\text{ N}, 25\text{ N}),\ \ \vec F_2 = (10\text{ N}, 15\text{ N}) \end{equation*}

What are the magnitude and direction of their sum, also called the net force, \(\vec F_{\text{net}}\text{.}\)

Answer.

\(50\text{ N},\, 53.1^{\circ} \) counterclockwise from positive \(x \) axis.

Solution.

From the discusssion of this section, we know that the components of the sum can be easily obtained from the components of the summand.

\begin{align*} \amp F_{\text{net},x} = F_{1x} + F_{2x} = 20\text{ N} + 10\text{ N} = 30\text{ N}. \\ \amp F_{\text{net},y} = F_{1y} + F_{2y} = 25\text{ N} + 15\text{ N} = 40\text{ N}. \end{align*}

Therefore, the magnitude of the sum is

\begin{equation*} \text{Magnitude, } F_{\text{net}} = \sqrt{30^2 + 40^2} = 50\text{ N}. \end{equation*}

To get the direction, we find the angle first by

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{40}{30}\right) = 53.1^{\circ}. \end{equation*}

Since point \((30, 40)\) is in the first quadrant, the direction of the net force is counterclockwise from the positive \(x \) axis.

Example 3.80. Adding Two Forces Given in Magnitude-Direction Form.

Suppose a box is being pushed by two forces, which are given to us in magnitude-direction form in the \(xy\) plane:

\begin{equation*} \vec F_1 = (30\text{ N},\, \text{East}),\ \ \vec F_2 = (40\text{ N},\, \text{South}) \end{equation*}

Use coordinate axes with positive \(x \) towards East and positive \(y \) towards North. What are the magnitude and direction of their sum? Note: magnitude is not equal to \(70\text{ N}\text{.}\)

Answer.

\(50\text{ N},\, 53.1^{\circ} \) clockwise from positive \(x \) axis.

Solution.

We will need to first write the given forces in their component forms. Let \(x \) axis be towards East and the \(y \) axis towards North. Then, here the component forms of the two given forces are easy to work out.

\begin{align*} \amp \vec F_1 = (30\text{ N},\ 0),\\ \amp \vec F_2 = (0,\ -40\text{ N}) \end{align*}

Let’s write \(\vec F \) for the sum vector. The components of the sum are then

\begin{align*} \amp F_{x} = F_{1x} + F_{2x} = 30\text{ N} + 0 = 30\text{ N}. \\ \amp F_{y} = F_{1y} + F_{2y} = 0 + (-40\text{ N}) = -40\text{ N}. \end{align*}

Therefore, the magnitude of the sum is

\begin{equation*} \text{Magnitude, } F_{\text{net}} = \sqrt{30^2 + 40^2} = 50\text{ N}. \end{equation*}

To get the direction, we find the angle first by

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{-40}{30}\right) = - 53.1^{\circ}. \end{equation*}

Since point \((30, -40)\) is in the fourth quadrant, the direction of the net force is clockwise from the positive \(x \) axis.

Exercises 3.3.3 Exercises

1. Adding Two Force Vectors.

Consider two force vectors, \(\vec F_1 \) that has a magnitude \(25.0\text{ N}\) in the direction of East, and \(\vec F_2 \) that has a magnitude \(40.0\text{ N}\) in the direction of \(30^{\circ}\) North of East. What are the magnitude and direction of their sum, \(\vec F_1 + \vec F_2\text{?}\) For stating directions in space, let \(x \) axis be pointed towards East, \(y \) axis be pointed towards North, and \(z \) axis be pointed Up.

Hint.

Add \(x \) components separately from the \(y \) components.

Answer.

\(62.9\text{ N}, 18.6^{\circ} \) counterclockwise from East towards North.

Solution.

First we find the component forms of each vector, and then will sum components in each direction separately.

\begin{align*} \amp F_{1x} = 25.0\text{ N},\ \ F_{1y} = 0,\\ \amp F_{2x} = 40.0 \cos\, 30^{\circ} = 34.6\text{ N}, \\ \amp F_{2y} = 40.0 \sin\, 30^{\circ} = 20.0\text{ N}, \end{align*}

Now, adding values along each axis separartely, we get \(x \) and \(y \) components of the sum. Let us denote them by \(F_x \) and \(F_y\text{.}\)

\begin{align*} \amp F_{x} = F_{1x} + F_{2x} = 25.0 + 34.6 = 59.6\text{ N},\\ \amp F_{y} = F_{1y} + F_{2y} = 20.0\text{ N}, \end{align*}

From these components, we can get the magnitude and direction. Since the values of \(F_x \) and \(F_y\) places the vector in the first quadrant, the angle will just be the counterclockwise from the positive \(x \) axis.

\begin{align*} \amp \text{Magnitude, }F = \sqrt{F_{x}^2 + F_{y}^2 } = \sqrt{59.6^2 + 20.0^2} = 62.9\text{ N},\\ \amp \theta = \tan^{-1}\left( \dfrac{F_y}{F_x} \right) = \tan^{-1}\left( \dfrac{20}{59.6} \right) = 18.6^{\circ}. \end{align*}

2. Adding Forces Using an Organizing Table.

Suppose we want to add three forces shown in Figure 3.81.

(1) \(15.0\text{ N} \) force pointed down, (2) \(12\text{ N} \) force pointed \(54^{\circ}\) below horizon, and (3) \(10.0 \text{ N} \) force pointed up.

(a) Organize the components of these forces in a table and find the components of the sum.

(b) Find the magnitude and direction of the sum.

Hint.

Find the components and make a table with three columns - name, \(x \) component, \(y\) component.

Answer 1. (a)

(a) \(( 7.05\text{ N}, -14.7\text{ N})\text{,}\)

Answer 2. (b)

(b) \(16.30\text{ N}, \) \(64.4^{\circ}\) clockwise from the positive \(x \) axis in the fourth quadrant.

Solution 1. a

We can make the following table to help us organize the components

Table 3.82. Force Components

Force	\(x\)-component	\(y\)-component
\(F_1 \)	\(0\)	\(-15.0\text{ N}\)
\(F_2 \)	\(12\text{ N}\, \cos\, 54^{\circ}=7.05\text{ N}\)	\(-12\text{ N}\, \sin\, 54^{\circ}=-9.71\text{ N}\)
\(F_3\)	0	\(10\text{ N}\)

From this table we find the components of the sum.

\begin{align*} \amp F_x = 0 + 7.05\text{ N} + 0 = 7.05\text{ N},\\ \amp F_y = -15.0\text{ N}-9.71\text{ N}+10\text{ N} = -14.7\text{ N}. \end{align*}

Solution 2. b

We use the components and find the magnitude to be

\begin{equation*} F = \sqrt{F_x^2 + F_y^2} = \sqrt{7.05^2 + 14.7^2 } = 16.30\text{ N}, \end{equation*}

and the angle with respect the the \(x \) axis

\begin{equation*} \theta = \tan^{-1}\left( \dfrac{-14.7}{7.05} \right) = - 64.4^{\circ}, \end{equation*}

which means \(64.4^{\circ}\) clockwise from \(+x\) axis in the fourth quadrant.

3. Adding Three Velocity Vectors.

Consider the following three velocity vectors:

\begin{align*} \amp \vec v_1 = \left(25.0\text{ m/s},\text{ towards East} \right), \\ \amp \vec v_2 = \left(25.0\text{ m/s},\ 30^{\circ}\text{ North of East} \right), \\ \amp \vec v_3 = \left(40.0\text{ m/s},\ 30^{\circ}\text{ North of West} \right). \end{align*}

What are the magnitude and direction of their sum, \(\vec v_1 + \vec v_2 + \vec v_3\text{?}\) For stating directions in space, let \(x \) axis be pointed towards East, \(y \) axis be pointed towards North, and \(z \) axis be pointed Up.

Hint.

Be careful with the signs. The \(v_{3x} \) should be negative.

Answer.

\(34.64\text{ m/s}, 69.7^{\circ} \)

Solution.

We start by working out the components of each of the three velocity vectors. The components of \(\vec v_1 \) and \(\vec v_2 \) do not give us any trouble.

\begin{align*} \amp v_{1x} = 25.0\text{ m/s},\ \ v_{1y} = 0\\ \amp v_{2x} = 21.65\text{ m/s},\ \ v_{2y} = 12.5\text{ m/s} \end{align*}

However, we need to be careful when we work on \(\vec v_3 \) since the vector is pointed in the second quadrant of the \(xy \) plane. When we peoject the arrow of the vector \(\vec v_3 \) on the \(x \) axis, we strike the negative \(x \) axis, which means that \(v_{3x} \lt 0 \text{,}\) i.e., negative.

\begin{align*} \amp v_{3x} = -v_3\, \cos(|\theta|) = -34.64\text{ m/s}\\ \amp v_{3y} = +v_3\, \sin(|\theta|) = +20.0\text{ m/s} \end{align*}

The components of the sum, to be written as \(v_x \) and \(v_y\) will be

\begin{align*} \amp v_{x} = v_{1x} + v_{2x} + v_{3x} = 25.0+21.65-34.64 = 12.0\text{ m/s},\\ \amp v_{y} = v_{1y} + v_{2y} + v_{3y} = 0 + 12.5 + 20 = 32.5\text{ m/s}. \end{align*}

This results in the following magnitude and angle

\begin{align*} \amp v = \sqrt{v_{x}^2 + v_y^2} = 34.64\text{ m/s},\\ \amp \theta = \tan^{-1}\left( \dfrac{v_y}{v_x}\right) = 69.7^{\circ}. \end{align*}

4. Adding Three Velocity Vectors.

Three velocity vectors fall in the \(xy\)-plane of a coordinate system and have the following representations: \(\vec V_1 = (3\ \textrm{m/s})\hat u_x + (2\ \textrm{m/s})\hat u_y\text{,}\) \(\vec V_2 = (9\ \textrm{m/s})\hat u_x + (11\ \textrm{m/s})\hat u_y\text{,}\) and \(\vec V_3 = (-8\ \textrm{m/s})\hat u_y\text{.}\) (a) Find the \(x\) and \(y\)-components of the sum of the three vectors. (b) Determine the magnitude and direction of the sum.

Solution 1. a

Let us denote the sum by symbol \(\vec V\text{.}\) The \(x\)- and \(y\)-components of the sum will be equal to the sum of the \(x\)- and \(y\)-components of the other vectors.

\begin{align*} \amp V_x = (3\ \textrm{m/s}) + (9\ \textrm{m/s}) = 12\ \textrm{m/s}\\ \amp V_y = (2\ \textrm{m/s}) + (11\ \textrm{m/s}) + (-8\ \textrm{m/s}) = 5\ \textrm{m/s}. \end{align*}

Solution 2. b

The magnitude of the sum vector = \(\sqrt{V_x^2 + V_y^2} = 13\ \textrm{m/s}\text{.}\) The direction will be in the first quadrant of the \(xy\)-plane. We can denote the direction here by the angle \(\theta\) that the vector \(\vec V\) makes with respect to the positive \(x\)-axis as we have done before.

\begin{equation*} \theta = \tan^{-1}\left( \frac{V_y}{V_x}\right) = 23^{\circ}. \end{equation*}

5. Adding Three Force Vectors.

Three force vectors fall in the \(yz\)-plane of a coordinate system and have the following representations: \(\vec V_1 = (100\ \textrm{N})\hat u_y + (200\ \textrm{N})\hat u_z\text{,}\) \(\vec V_2 = (-500\ \textrm{N})\hat u_y + (100\ \textrm{N})\hat u_z\text{,}\) and \(\vec V_3 = (-400\ \textrm{N})\hat u_y+ (500\ \textrm{N})\hat u_z\text{.}\) (a) Find the \(y\) and \(z\)-components of the sum of the three vectors. (b) Determine the magnitude and direction of the sum.

Solution 1. a

Let us denote the sum vector here by the symbol \(\vec F\text{.}\) The \(y\)- and \(z\)-components of the sum will be equal to the sum of the \(y\)- and \(z\)-components of the other vectors.

\begin{align*} \amp F_y = (100\ \textrm{N}) + (-500\ \textrm{N}) + (-400\ \textrm{N}) = (-800\ \textrm{N})\\ \amp F_z = (200\ \textrm{N}) + (100\ \textrm{N}) + (500\ \textrm{N}) =(800\ \textrm{N}). \end{align*}

Solution 2. b

The magnitude of the sum vector = \(\sqrt{F_y^2 + F_z^2} = 800\sqrt{2}\ \textrm{N}\text{.}\)

Here we can choose to describe the direction by the angle a vector makes with the positive \(y\) axis in a counterclockwise sense as we look at the \(yz\) plane from positive \(x\) axis direction. The direction will be in the second quadrant of the \(yz\)-plane. We can denote the direction here by the angle \(\theta\) that the vector \(\vec F\) makes with respect to the positive \(y\)-axis.

\begin{equation*} \theta = \tan^{-1}\left( \frac{F_z}{F_y}\right) + 180^{\circ}= 135^{\circ}. \end{equation*}

Note that I have added \(180^{\circ}\) to convert the angle I obtained from the arctangent so that the angle refers to the angle with respect to the positive \(y\)-axis.

6. Find Components and Add Forces.

(a) Find the \(x\) and \(y\)-components of the two forces given in Figure 3.84 with respect to the coordinates given in the figure. (b) Add the two vectors and find the magnitude and direction of the resultant vector.

Solution 1. a

Let \(\vec F_1\) be the vector at \(60^{\circ}\) from the \(x\) axis and \(\vec F_2\) be the other vector.The components of \(\vec F_1\) and \(\vec F_2\) are

\begin{align*} \amp F_{1x} = (100\ \textrm{N}) \cos(60^{\circ}) = 50\ \textrm{N}\\ \amp F_{1y} = (100\ \textrm{N}) \sin(60^{\circ}) = 86.6\ \textrm{N}\\ \amp F_{2x} = -100\ \textrm{N}\\ \amp F_{2y} = 0 \end{align*}

Solution 2. b

The sum of these vectors, to be denoted by \(\vec F\) will have the following components.

\begin{align*} \amp F_{x} = (50-100)\ \textrm{N} = -50\ \textrm{N}\\ \amp F_{y} = 86.6\ \textrm{N} \end{align*}

From these components we construct the magnitude of the net vectors to be

\begin{equation*} F = \sqrt{F_x^2 +F_y^2} = \sqrt{(-50\ \textrm{N})^2 + (86.6\ \textrm{N})^2 } = 100\ \textrm{N}. \end{equation*}

The direction of this vector can be given by the angle with respect to the positive \(x\) axis. Since the \(x\)-component is negative and the \(y\)-component is positive, the vector will fall in the second quadrant. To obtain the counterclockwise angle from the arctangent of ratio of y to x we will need to add \(180^{\circ}\) to the answer.

\begin{equation*} \theta = 180^{\circ} + \tan^{-1}\left( \frac{-50}{86.6}\right) = 180^{\circ} - 30^{\circ} = 150^{\circ}. \end{equation*}

Prev Top Next