Static Friction

Section 6.11 Static Friction

We are all familiar with warming of hands when we rub our hands together. This is due to the friction between the skins of the two hands. If you hold your hands pressed against each other and try to gently slide on top of the other, they may not slide. The friction when they are not sliding is called static friction and when sliding it’s called kinetic friction.

Static and kinetic frictions are possible between every two solid bodies in contact. The fundamental reason of friction is a net force of attraction between the molecules at the surface of the two bodies. When you attempt to slide one body over the other, these bonds stretch out a little, which creates additional attractive force between the two bodies as illustrated in Figure 6.41. This additional attractive force is the source of friction between the two bodies.

Figure 6.41. Static fricion force opposes the applied force. When acting on the body on which the applied force is acting, it is in the opposite direction to the applied force. But when acting on the other object, here the table, the static friction force is in the same direction as the applied force. *Without the applied force that is attempting to slide the two bodies over each other, there is no static friction between them since molecular bonds are in relaxed state.*

In this section we will look at the static friction and defer discussion of kinetic friction to another secton. We will denote static friction force by symbol \(\vec F_s\) and the magnitude by the same symbol without an arrow.

Just as the normal force, there is no formula for the magnitude of static friciton force. Here, if you have memorized any formula for \(F_s\text{,}\) it would be better to forget them. For instance, a common wrong formula students often memorize is \(F_s = \mu_s F_N \text{.}\) This formula is only correct when \(F_s \) takes the maximum value \(F_s^\text{max} \) as discussed below. In general, \(F_s\) can take any value between zero and \(F_s^\text{max}\text{,}\) which is \(\mu_s F_N\text{,}\) \(0 \le F_s \le F_s^\text{max} \text{.}\)

The direction of the static friction force is obtained by the attractive nature of the force and that the force is pointed in the plane of the contact surface if the contact is planar or in the tangent plane if the surface of contact is curved.

Just like the normal force, static friction force may vary across the surface of contact. When making a diagram in which we draw one arrow for the static friction force, we will draw the arrow near locations where we expect the largest value.

Subsection 6.11.1 Maximum Static Friction Force

In the example of book on the table in Figure 6.41, as you push the book gently, say with increasing force. You find that, your force is balanced by the static friction force up to a limit; but, if the applied force is above that limit, the book starts to slide on the table.

These observations mean that, under a given condition, there can be only so much static friction before the bodies start to slide. We denote the magnitude of this maximum static friction by \(F_s^{\text{max}} \text{.}\)

We can find the value of \(F_s^{\text{max}} \) experimentally by measuring static friction for various applied forces. You can plot static friction for various applied forces, which will terminate when applied force leads to sliding. The termination point will give the value of \(F_s^\text{max}\text{.}\)

The ratio of \(F_s^{\text{max}} \) to the magnitude of the normal force \(F_N \) for a surface turns out to be a characteristic of the surface of contact. We call this ratio the coefficient of static friction and denote by the Greek letter \(\mu_s\) (read mu sub s).

\begin{equation} \mu_s = \dfrac{F_s^{\text{max}}}{F_N}.\tag{6.16} \end{equation}

If two surfaces are stuck together, then they cannot slide past each other. In that case \(\mu_s = \infty \text{,}\) and if you don’t need any force to slide, i.e., for a frictionless surface, \(\mu_s = 0 \text{.}\) That is, \(0 \le \mu_s \lt \infty\text{.}\)

Example 6.43. Determining Static Friction.

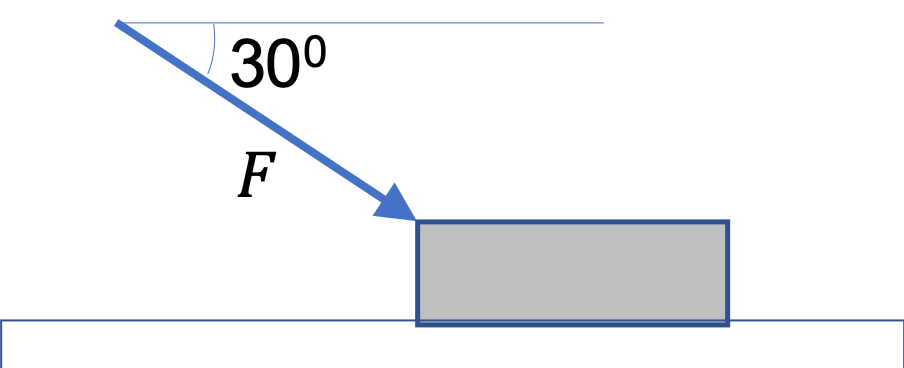
A book of mass \(1.5\text{ kg}\) is at rest on a horizontal table. The book is then pushed with a constant force of \(12\text{ N}\) at an angle of \(30^{\circ}\) below the horizontal direction, which is not enough to overcome the static friction between the book and the table.

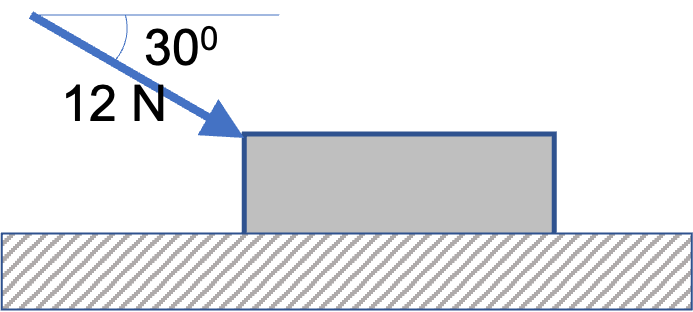
(a) Find all the forces on the book.

(b) Using your answer in (a) determine the force on the table by the book.

Answer.

(a) \(F_s = 10.39\text{ N},\ \ F_N = 20.715\text{ N}. \text{,}\) (b) \(23.2 \text{ N}, 63.4^{\circ}\text{ below } x\text{ axis}\text{,}\) (c) Not do-able based on the given information, since we need the maximum static friction, not just any static friction.

Solution 1. a

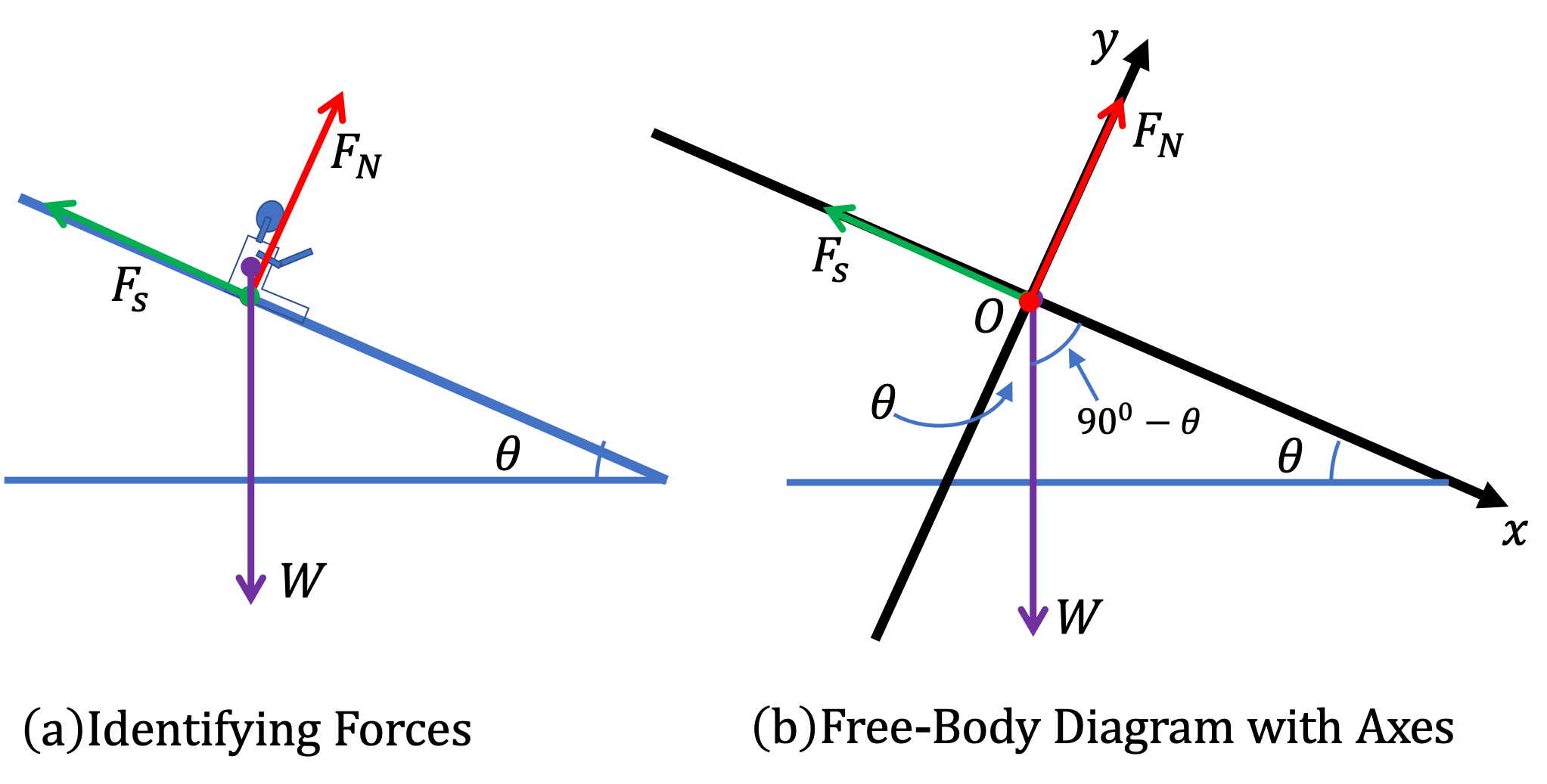
System : Book.

Identify and list the forces on the system:

We first try to identify forces on the box and use a diagram as shown in Figure 6.45(a). Then, we redraw a sketch of just the forces, all coming out of the same point as in Fig. Figure 6.45(b).

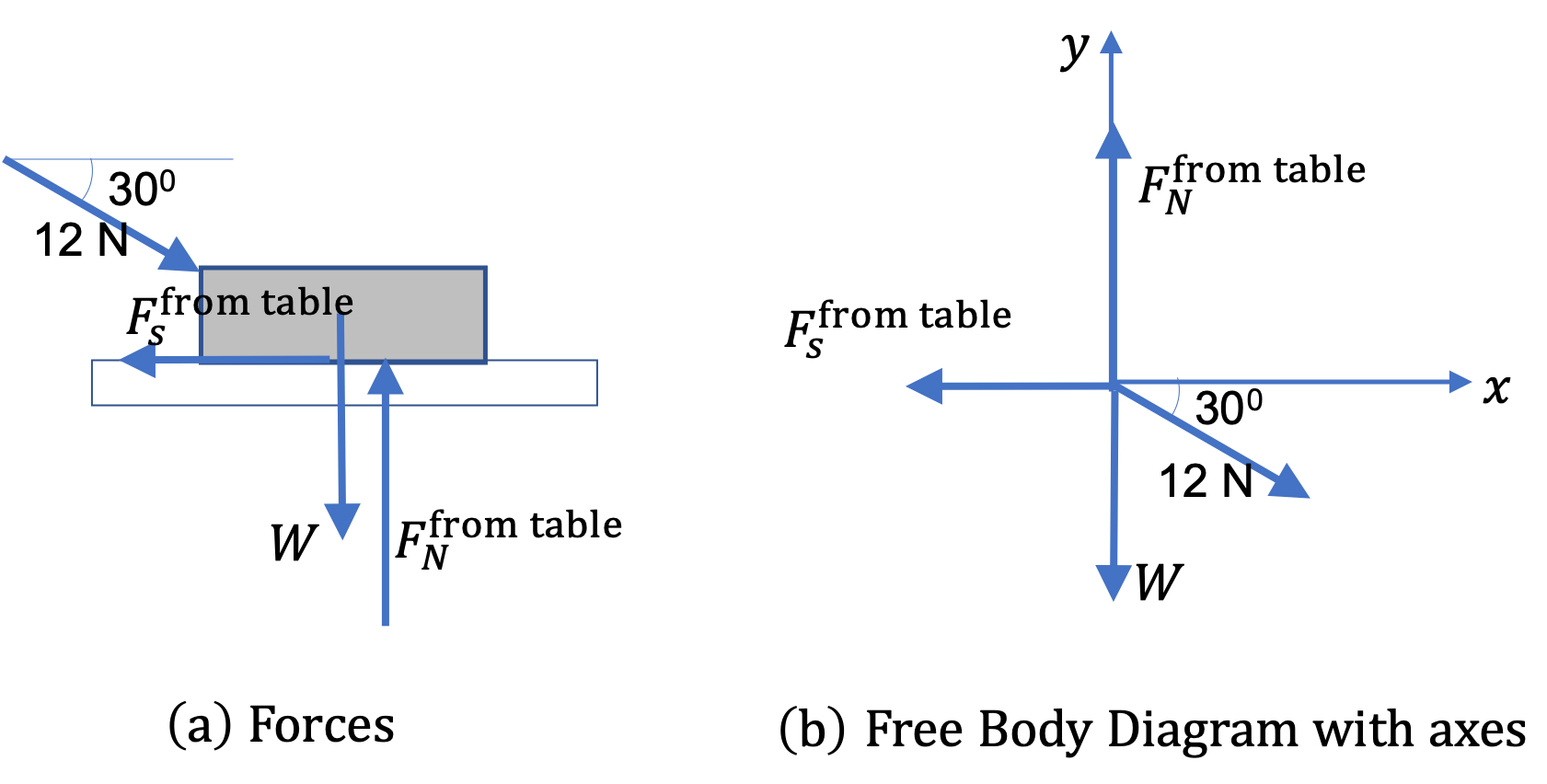
Figure 6.45. (a) Sketch of forces on the box along with the box, floor, and wall. (b) Redrawing the forces in a simpler figure of just the forces in the free-body diagram. Choice of axes is also shown in (b).

Choose Cartesian coordinates:

Since \(\vec a = 0 \text{,}\) our guide for direction of axes is the axes that will simplify computing the components of forces easier.

Generate equations of motion:

We now collect the \(x \) and \(y \) components of forces in a table.

Table 6.46. Forces on the Book

Force	\(x\)-component	\(y\)-component
Weight	\(0\)	\(-14.715\text{ N}\)
Applied Force	\(12\text{ N}\, \cos\, 30^{\circ}\)	\(-12\text{ N}\, \sin\, 30^{\circ}\)
Normal from the table	0	\(F_N\)
Static friction from the table	\(-F_s\)	\(0\)

Since the acceleration of the book is zero, the net force on the book must be zero. That means, \(x \) and \(y \) components of net force will be separately zero.

\begin{align*} \amp F_{x}^{\text{net}} = 0 + 10.39 + 0 - F_s = 0.\\ \amp F_{y}^{\text{net}} = - 14.715 - 6.0 + F_N + 0 = 0. \end{align*}

Solve for the desired quantities:

Solving the unknowns in the equations of motion, we get the following after putting the units back in.

\begin{equation*} F_s = 10.39\text{ N},\ \ F_N = 20.72\text{ N}. \end{equation*}

Interpret the result:

The normal force on the book from the table has magnitude \(20.72\text{ N}\) pointed up, and the static friction on the book from the table has magnitude \(10.39\text{ N}\) pointed in horizontally to oppose the tendency of the applied force.

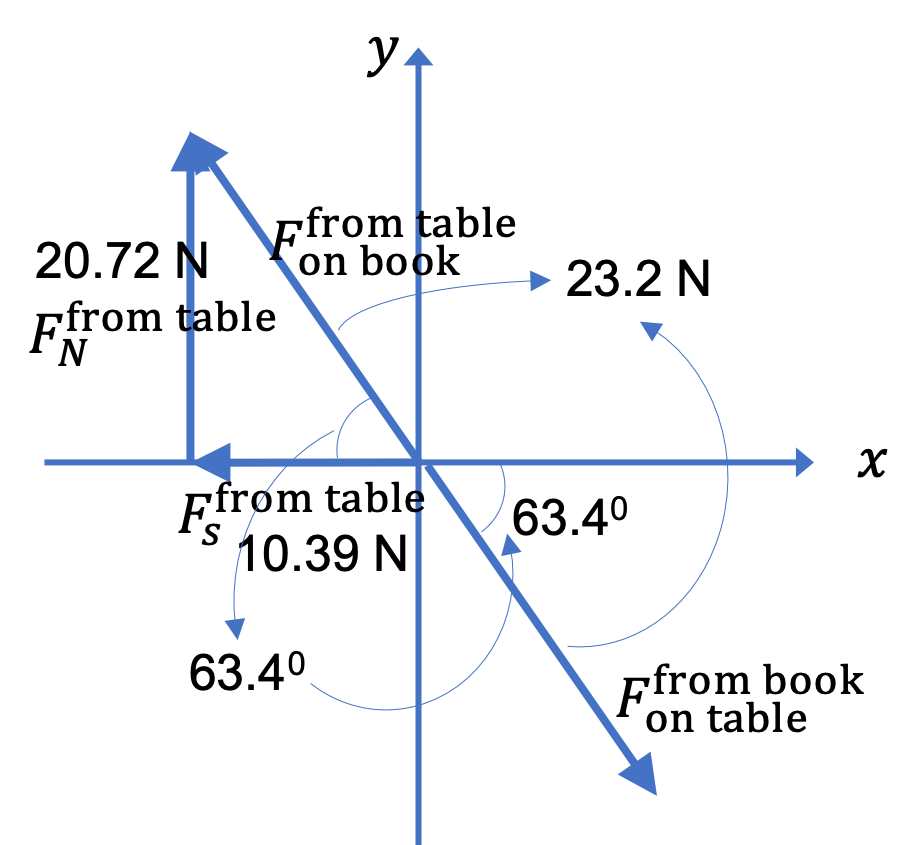
Solution 2. b

In part (a), we found two forces applied by the table on the book. Their vector sum will give the net force by the table on the book.

The required force, the force by the book on the table, is the negative of this force with the following components.

\begin{equation*} F_x = + 10.39\text{ N}, \ \ F_y = -20.72\text{ N}. \end{equation*}

The magnitude is \(\sqrt{10.39^2 + 20.72^2} = 23.2\text{ N}\) and angle \(\theta \) is \(\tan^{-1}(-20.715/10.39) = - 63.4^{\circ}\text{.}\) Since point \((10.39, -20.72) \) is in the fourth quadrant, the direction of this force is \(63.4^{\circ}\) clockwise from the positive \(x \) axis.

Solution 3. c

We cannot answer this question based on the information provided since for \(\mu_s\) we need the maximum static friction \(F_s^{\text{max}}\) which we do not have. We do not know how much more applied force the book can take before starting to slide.

Example 6.47. Maximum Static Friction.

A book of mass \(1.5\text{ kg}\) is at rest on a horizontal table. The book is then pushed with a force at an angle of \(30^{\circ}\) below the horizontal direction.

When magnitude of the force is increased, we find that, once the magnitude reaches \(25\text{ N}\text{,}\) the book starts to slide on the table.

(a) What are the magnitudes of normal and static friction forces between the book and the table?

(b) What is the value of the coefficient of static friction force between the book and the table?

Answer.

(a) \(F_N = 27.22\text{ N},\ \ F_s = 21.65\text{ N}\text{,}\) (b) 0.8.

Solution 1. a

We follow exact same steps explained in Example 6.43. They lead to the following equations of motion. You should work out the detials.

\begin{equation*} F_N = 27.22\text{ N},\ \ F_s = 21.65\text{\text N}. \end{equation*}

Solution 2. b

This \(F_s\) is actually \(F_s^{\text{max}} \) since the book will slide if the applied force was any greater.

\begin{equation*} F_s^{\text{max}} = 21.65\text{\text N}. \end{equation*}

From \(F_s^{\text{max}} \) and \(F_N\) we get \(\mu_s \text{.}\)

\begin{equation*} \mu_s = \dfrac{F_s^{\text{max}}}{F_N} = \dfrac{21.65}{27.22} = 0.8. \end{equation*}

Exercises 6.11.2 Exercises

1. Finding Coeficient of Static Friction.

A child is sitting at rest at a wooden board. When the angle of incline of the board is increased, the child starts to slide when the angle is \(30^{\circ}\text{.}\)

(a) What is the coefficient of static friction between the pants of the child and the board?

(b) You will get the same coefficient of static friction regardless of the mass of the child. Explain why.

Hint.

(a) Find maximum static friction by using \(\vec F_{\text{net}} = 0\text{,}\) (b) Think of the surface of contact.

Answer.

(a) \(\dfrac{1}{\sqrt{3}} \approx 0.577\text{,}\) (b) \(\mu\) is between the cloth and the board.

Solution 1. a

Developing Ideas for Solution:

We notice that the condition at \(\theta = 30^{\circ}\) incline is when static friction must be at the maximum. \(F_s = F_s^{\text{max}}.\) Therefore, if we find the static friction and the normal force , \(F_N\text{,}\) we will calculate the desired quantity, \(\mu_s\) by

\begin{equation*} \mu_s = \dfrac{F_s^{\text{max}}}{F_N}. \end{equation*}

To find these forces, we use Newton’s second law with \(\vec a = 0\) since the child is not accelerating with respect to any inertial frame, such as the ground.

The observation \(\vec a = 0\) means we have

\begin{equation*} \vec F_{\text{net}} = 0, \end{equation*}

which would give us two component equations here. To get the components equations, we proceed in our standard way, by identifying the forces on the child, drawing a free-body diagram, choosing axes, finding expressions for the components of the foces, and then getting the sums of components along each axis.

Identifying Forces, Drawing Free-Body, and Choosing Axes:

Figure 6.50 below shows all these. There are three forces on the child - weight, normal, and static friction. By choosing one of the axes along the incline, we can make two of these forces to fall along axes. This reduces our work of finding components - we only need to figure out \(x\) and \(y\) components of weight only.

Figure 6.50. Figure for Exercise 6.11.2.1(a).

Working out Components and Getting Equations of Motion:

We only need to work for finding components of the weight vector. We notice that the weight vector is in the fourth quadrant, with angle \(\theta\) with the negative \(y\) axis. Projections of the weight vector on the axes will give a positive value for \(W_x\) and a negative value for \(W_y\) with \(W_y\) being adjacent to the angle \(\theta\text{.}\)

\begin{align*} \amp W_x = W\,\sin\,\theta \\ \amp W_y = -W\,\cos\,\theta, \ \ \text{Note the negative.} \end{align*}

For the other forces, we have

\begin{align*} \amp F_{Nx} = 0,\ \ F_{Ny} = F_N, \\ \amp F_{sx} = -F_s^{\text{max}},\ \ F_{sy} = 0, \ \ \text{Note the negative.} \end{align*}

From the components of forces, we get the two equations for the net force.

\begin{align} \amp W\,\sin\,\theta + 0 - F_s^{\text{max}} = 0, \tag{6.17}\\ \amp -W\,\cos\,\theta + F_N + 0 = 0.\tag{6.18} \end{align}

Solving Equations of Motion:

Solving Equations (6.17) and (6.18) we find the following for \(F_N \) and \(F_s^{\text{max}}\text{.}\)

\begin{equation*} F_N = W\,\cos\,\theta,\ \ F_s^{\text{max}} = W\,\sin\,\theta, \end{equation*}

from which we immediately obtain the coefficient of static friction.

\begin{equation*} \mu_s = \dfrac{F_s^{\text{max}}}{F_N} = \dfrac{W\,\sin\,\theta}{W\,\cos\,\theta} = \tan\,\theta. \end{equation*}

Putting the numerical value of \(\theta\) w get

\begin{equation*} \mu_s = \tan\,30^{\circ} = \dfrac{1}{\sqrt{3}} \approx 0.577. \end{equation*}

Solution 2. b

Interpreting the Result:

We notice that the weight canceled out. So, every child with the same cloth, regardless of their mass, will begin to slide at this angle of incline, since we are really finding the coefficient of static friction between the surface of the cloth and the board.

Prev Top Next