Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 24.6 First Law of Thermodynamics Bootcamp

Exercises Exercises

First Law of Thermodynamics

1. Work Done in a Constant Pressure Process.
Follow the link: Example 24.5.
2. Work Done by an Ideal Gas in a Constant Temperature Process.
Follow the link: Example 24.6.
4. Heat Flow in Heating Liquid Water.
Follow the link: Example 24.10.
5. Heat Flow into a Copper Block While Melting the Block.
Follow the link: Example 24.11.
6. Work, Heat, and Internal Energy in a Thermal Expansion of Steam.
Follow the link: Example 24.12.
7. Work, Heat and Internal Energy Change in Processes in a Gas.
Follow the link: Example 24.14.
8. Work, Heat, and Internal Energy in a Cyclic Process.
Follow the link: Example 24.16.

Ideal Gas Adiabatic Processes

9. Work Done by an Ideal Gas in an Adiabatic Process.
Follow the link: Example 24.20.
10. Adiabatic Expansion of a Monatomic Ideal Gas.
Follow the link: Example 24.21.
11. Work in Adiabatic and Isothermal Expansions of an Ideal Gas.
Follow the link: Exercise 24.3.1.
12. Internal Energy Change in Adiabatic Compression of an Ideal Gas.
Follow the link: Exercise 24.3.2.
13. Internal Energy Change in Quasistatic Adiabatic Compression of an Ideal Gas.
Follow the link: Exercise 24.3.3.
14. Internal Energy Change in Adiabatic Expansion of an Ideal Gas.
Follow the link: Exercise 24.3.4.

Calorimetry

Enthalpy and Joule-Thomson Effect

15. Enthalpy Change in Heating Water at Constant Pressure.
Follow the link: Example 24.22.
16. Changes in Inernal Energy and Enthalpy in a Gas Expansion Process.
Follow the link: Example 24.23.
17. Changes in Inernal Energy and Enthalpy in Isothermal Expansion.
Follow the link: Exercise 24.4.2.1.
18. Changes in Inernal Energy and Enthalpy in Isobaric Expansion.
Follow the link: Exercise 24.4.2.2.
19. Change in Internal Energy and Temperature in a Joule-Thomson Throttling Process.
Follow the link: Example 24.25.
20. Cooling a Helium Gas in a Joule-Thomson Throttling Process.
Follow the link: Exercise 24.5.1.

Miscellaneous

21. Mechanical Equivalence of Heat Experiment.
In the Joule mechanical equivalence of heat experiment, a \(30\) W motor powers the paddles. The paddles heat up \(1\times10^{-3}\, \text{m}^3\) water and \(200\) g of copper container. What will be the increase in temperature of water if the motor is run for \(30\) minutes, and \(5\%\) of the energy used by the motor is lost as heating in the motor.
Solution.
Here \(95\%\) of the energy into the motor goes towards raising the temperature of the water and the container. Let us denote the power of the motor by \(P\) and the duration by \(\Delta t\text{.}\) Let the specific heats of water and copper be denoted by \(c_1\) and \(c_2\) respectively, and the rise in temperature by \(\Delta T\text{.}\) Let the corresponding masses be \(m_1\) and \(m_2\text{.}\) Then we will have
\begin{equation*} P \Delta t = \left( m_1 c_1 + m_2 c_2 \right) \Delta T \end{equation*}
Therefore
\begin{equation*} \Delta T = \frac{P \Delta t }{ m_1 c_1 + m_2 c_2}. \end{equation*}
Now, we put in the numbers.
\begin{align*} \amp P = 30\ \textrm{W}\\ \amp \Delta t = 1800\ \textrm{s}\\ \amp m_1 = 1.0\ \textrm{kg}\ \ \textrm{(using density = 1 g/cc)}\\ \amp m_2 = 0.2\ \textrm{kg}\\ \amp c_1 = 4180\ \textrm{J.kg}^{-1}\,^{\circ}\text{C}^{-1}\\ \amp c_2 = 390\ \textrm{J.kg}^{-1}\,^{\circ}\text{C}^{-1} \end{align*}
These give the value \(\Delta T = 12.7^{\circ}\textrm{C}\text{.}\)
22. An Adiabatic Process Connecting Two Isotherms.
On an adiabatic process of an ideal gas pressure, volume and temperature change such that \(pV^{\gamma}\) is constant with \(\gamma = 5/3\) for monatomic gas such as helium and \(\gamma = 7/5\) for diatomic gas such as hydrogen at room temperature. Use numerical values to plot two isotherms of 1 mole of helium gas using ideal gas law and two adiabatic processes mediating between them. Use \(T_1=500\textrm{K}\text{,}\) \(V_1=1\textrm{ L}\text{,}\) and \(T_2=300\textrm{K}\) for your plot.
Solution.
One adiabatic process mediating two isotherms are shown in the figure below. In drawing the adiabatic I choose the initial state on the upper isotherm and changed volume according to the rule of the adiabatic expansion. You can try to draw the other adiabatic that starts at a different place on the upper isotherm.
Figure 24.26.
23. Analyzing the Thermodynamics of an Ideal Gas Process.
A monatomic ideal gas undergoes a quasi-static process which is described by the function \(p(V) = p_1 + 3\left(V-V_1 \right)^2\text{,}\) where the starting state is \((p_1,V_1)\) and the final state \((p_2, V_2)\text{.}\) Assume the system consists of \(n\) moles of the gas in a container which can exchange heat with the environment and whose volume can change freely. (a) Evaluate the work done by the gas during the change in the state. (b) Find the change in internal energy of the gas. (c) Find the heat input to the gas during the change. (d) What are initial and final temperatures?
Solution 1. a
The work done by the gas
\begin{align*} W \amp = \int p dV = \int \left[ p_1 + 3\left(V-V_1 \right)^2\right]\, dV\\ \amp = \left. \left(p_1 + 3 V_1^2 \right) V - 3V_1 V^2 + V^3 \right|_{V_1}^{V_2}\\ \amp = \left(p_1 + 3 V_1^2 \right) \left( V_2 - V_1 \right) - 3V_1 \left( V_2^2 - V_1^2 \right) + \left( V_2^3 - V_1^3 \right). \end{align*}
Solution 2. b
Since the gas is a monatomic ideal gas, the change in the internal energy can be given in terms of the change in temperature.
\begin{equation*} \Delta U = \frac{3}{2} n R \left( T_2 - T_1\right) = \frac{3}{2} \left( p_2V_2 - p_1V_1\right). \end{equation*}
Solution 3. c
From the first law
\begin{equation*} Q = \Delta U + W, \end{equation*}
where \(\Delta U\) and \(W\) are given in (b) and (a) respectively.
Solution 4. d
The initial and final temperatures can be obtained by applying the ideal gas equation to these states.
\begin{equation*} T_1 = \frac{p_1 V_1}{n R},\ \ T_2 = \frac{p_2 V_2}{n R}. \end{equation*}
24. Work by Gases in Two Chambers Separated by a Movable Wall.
A metallic container of fixed volume of \(2.5 \times 10^{-3}\,\text{m}^3\) immersed in a large tank of temperature \(27^{\circ}\text{C}\) contains two compartments separated by a freely movable wall. Initially the wall is kept in place by a stopper so that there are 0.02 moles of the Nitrogen gas on one side and \(0.03\) moles of the Oxygen gas on the other side, each occupying half the volume. When the stopper is removed, the wall moves and comes to a final position. The movement of the wall is controlled so that the wall moves in infinitesimal quasi-static steps. (a) Find the final volumes of the two sides assuming the ideal gas behavior for the two gases. (b) How much work does each gas does on the other? (c) What is the change in the internal energy of each gas? (d) Find the amount of heat that enters or leaves each gas.
Solution 1. a
The process is a constant temperature process since the container is in thermal contact with a large heat bath whose temperature is constant. At the end of the process the pressures of the two sub-systems become equal since the net force on the separating wall becomes zero.
Figure 24.27.
Let the common temperature and pressure on the two sides after coming to equilibrium be denoted by \(T\) and \(p\) respectively. When the gases have come to an equilibrium their equations of states are
\begin{align*} \amp p V_1 = n_1 RT\\ \amp p V_2 = n_2 RT \end{align*}
Therefore
\begin{equation} \frac{V_1}{V_2} = \frac{n_1}{n_2}.\tag{24.33} \end{equation}
Let us denote the total volume by \(V_0\text{.}\)
\begin{equation} V_1 + V_2 = V_0.\tag{24.34} \end{equation}
From Eqs. (24.33) and (24.34) we obtain
\begin{align*} \amp V_1 = \frac{n_1}{n_1 + n_2} V_0.\\ \amp V_2 = \frac{n_2}{n_1 + n_2} V_0. \end{align*}
Using the given numbers we get (writing \(1\, \text{L}\) for \(10^{-3}\,\text{m}^3\))
\begin{equation*} V_1 = \frac{3}{5}\times 2.5\ \textrm{L} = 1.5\ \textrm{L},\ \ \ V_2 = \frac{2}{5}\times 2.5\ \textrm{L} = 1.0\ \textrm{L}. \end{equation*}
Solution 2. b
Since the process for each gas is a constant pressure process, it is easy to integrate \(pdV\) using the ideal gas to replace \(p\) in the integrand. The work done by the gas in the compartment 1 is found to be
\begin{equation*} W_{\textrm{by 1}} = n_1 RT\ln\left( V_f^{(1)}/V_i^{(1)}\right) = n_1 RT\ln\left(\frac{2n_1}{n_1 + n_2}\right). \end{equation*}
Putting in the numbers now
\begin{equation*} W_{\textrm{by 1}} = 0.03\ \textrm{mol}\times \frac{8.31\ \textrm{J}}{\textrm{mol.K}}\times 300.15\ \textrm{K}\ln\left(\frac{2\times 0.03}{0.03 + 0.02}\right) = 13.6\ \textrm{J}. \end{equation*}
Solution 3. c
Since the process is isothermal and the system is ideal gas, \(\Delta U = 0\text{.}\)
Solution 4. d
The heat entering system (1), which is the side with the Oxygen gas here, will be equal to the work by this side.
\begin{equation*} Q_1 = \Delta U_1 + W_{\textrm{by 1}} = 13.6\ \textrm{J}. \end{equation*}
25. Two Different Ways to Transform States Give Same Internal Energy Change But Different Work and Heat.
A gaseous system goes from a state A to another state B on a curve \(pV^{1.8}\) = constant in the \(pV\) plane as shown in Figure 24.28. Alternately, we go from A to B by first lowering the pressure at constant volume to C and then heat at constant pressure to B as shown.
(for accessibility)
Figure 24.28.
(a) Find the amount of work done on the A-C-B path. (b) Find the amount of heat exchanged by the system when it goes from A to B on A-C-B path. (c) Compare the change in the internal energy when A-B process occur via the A-B path versus the two-step A-C-B path.
Solution 1. a
The work done on path A-C-B is easy to do if you recognize that no work is done on the constant volume part A-C. The work in teh C-B part will be just the product of the constant pressure and the volume change.
\begin{equation*} W_{ACB} = p_2(V_2-V_1). \end{equation*}
We do need to work out the pressure \(p_2\text{.}\) Since A and B are related by an adiabatic process the pressures and volumes at those points are related by
\begin{equation*} p_1 V_1^{\gamma} = p_2 V_2^{\gamma}. \end{equation*}
Therefore
\begin{equation*} W_{ACB} = p_1(V_2-V_1)\left( \frac{V_1}{V_2} \right)^{\gamma} = 16.4\ \textrm{L.atm} = 1660\textrm{J}. \end{equation*}
Solution 2. b
The difference of the internal energy between states A and B was obtained in the last problem. The change in internal energy will be same regardless of how you go from A to B.
\begin{equation*} \Delta U = -4.39 \textrm{MJ}. \end{equation*}
Using the first law now we find that heat into the system when the system goes in the path A-C-B is
\begin{equation*} Q = \Delta U + W = -4.39\ \textrm{kJ} + 1660\ \textrm{J} = -2730\ \textrm{J}, \end{equation*}
where \(W_{ACB}\) is given above.
Solution 3. c
The change in internal energy must be same for the two paths between same two sates since \(U\) is a state function and depends on the state variables and not on paths.
26. Work, Heat, and Energy Change in a Cyclic Process.
Two moles of monatomic ideal gas at (\(5\) MPa, \(5\) L) is expanded isothermally until the volume is doubled as shown in Figure 24.29. Then, it is cooled isochorically till the pressure is \(1\) MPa. The temperature drops in this process. The gas is now compressed isothermally till its volume is back to \(5\) L, but its pressure is now \(2\) MPa. Finally, the gas is heated isochorically to return to the initial state.
Figure 24.29.
Find the total work done by the gas, the net change in the internal energy and the net heat entering the gas in the cycle.
Solution.
The work in the steps of the cycle will be
\begin{align*} \amp W_{12} = n RT_1 \ln\left( \frac{V_2}{V_1}\right)\ \ (\textrm{Isothermal Process})\\ \amp W_{23} = 0\ \ (\textrm{Isochoric Process})\\ \amp W_{34} = n RT_3 \ln\left( \frac{V_4}{V_3}\right)\ \ (\textrm{Isothermal Process})\\ \amp W_{41} = 0\ \ (\textrm{Isochoric Process}) \end{align*}
The net work will be the sum of these terms.
\begin{equation*} W_{12341} = W_{12} + W_{23} + W_{34} + W_{41}. \end{equation*}
Since in a cyclic process the system returns to the original state at the end of the cycle, the net change in the internal energy will be zero.
\begin{equation*} \Delta U_{\textrm{complete cycle}} = 0. \end{equation*}
Therefore, net heat into the system will equal the net work done.
\begin{equation*} Q = W _{12341}. \end{equation*}
You can put the numerical values in the formulas. Use ideal gas law at any one point on the cycle to relate pressure, volume and temperature at that point in the \(pV\)-plane.
27. Change in Internal Energy and Enthalpy of an Ideal Gas in a Isochoric Process.
An \(n\) moles of helium gas, assumed a monatomic ideal gas, contained in a rigid container with fixed volume is heated in a quasi-static process. As a result, the pressure inside the container doubles with respect to the initial pressure. (a) Find the change in the internal energy of the gas in terms of the initial temperature \(T_0\text{.}\) (b) Find the change in enthalpy of the gas in terms of the initial temperature \(T_0\text{.}\)
Solution 1. a
Since the volume is fixed, doubling the pressure will double the temperature in the absolute scale. Therefore, the change in the internal energy of the monatomic ideal gas will be
\begin{equation*} \Delta U = \frac{3}{2} n R (2T_0 - T_0) = \frac{3}{2} n R T_0. \end{equation*}
Solution 2. b
The change in the enthalpy will be
\begin{equation*} \Delta H = \Delta U + \Delta (p V). \end{equation*}
Let us work out \(\Delta (pV)\text{.}\)
\begin{equation*} \Delta (pV) = \Delta (n RT) = n R (2T_0-T_0) = n RT_0. \end{equation*}
Therefore
\begin{equation*} \Delta H = \Delta U + \Delta (p V) = \frac{5}{2} n R T_0. \end{equation*}
28. Equilibrium when Mixing Ice and Water.
A 100 g ice cube from freezer at \(-15^{\circ}\)C is dropped into 500-g water in a 250 g insulated aluminum container at \(20^{\circ}\)C. Find the temperature and phase of the final state.
Solution.
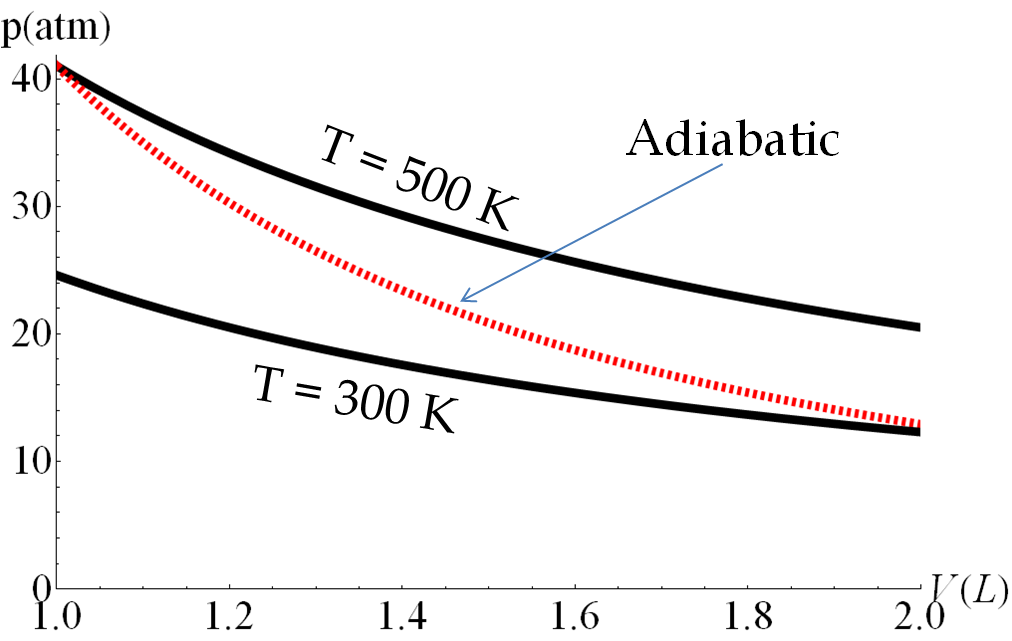
By a rough calculation, you can confirm that if the entire water were to come down in temperature to \(0^{\circ}\)C, the energy released would be enough to melt the ice and some energy will be left over. Therefore, the final state will consist of a mixture 600 g of water ata temperature T between \(0^{\circ}\)C and \(20^{\circ}\)C. Here are the rough calculations. [To simplify we ignore the energy involved with the container.
The energy needed to melt all ice into water:
\begin{align*} \amp \textrm{1. Raise the temp to }0^{\circ}\text{C}: \ 0.100\ \textrm{kg}\times \frac{\textrm{2000\ J}}{\textrm{kg. C}}\times 15^{\circ}\textrm{C}.\\ \amp \textrm{2. Melt the ice at }0^{\circ}\text{C}: \ 0.100\ \textrm{kg}\times \frac{\textrm{335,000\ J}}{\textrm{kg }}. \end{align*}
The total needed = 36,400 J.
The energy released when the temperature of the water comes down from \(20^{\circ}\)C to \(0^{\circ}\)C:
\begin{align*} \amp 0.500\ \textrm{kg}\times \frac{\textrm{4180\ J}}{\textrm{kg. C}}\times 20^{\circ}\textrm{C} = 41,800\ \textrm{J}. \end{align*}
That means we have more than enough energy to melt all ice and the final temperature will be above \(0^{\circ}\)C. Now, we can set up the equation for \(T\text{.}\)
\begin{align*} \amp 36,400 J + 0.1\ \textrm{kg}\times \frac{\textrm{4180\ J}}{\textrm{kg. C}}\times T\\ \amp \ \ \ \ \ \ \ \ \ =\left[ \ 0.500\ \textrm{kg}\times \frac{\textrm{4180\ J}}{\textrm{kg. C}} + 0.250\ \textrm{kg}\times \frac{\textrm{ 910\ J}}{\textrm{kg. C}} \right]\ \times (20-T). \end{align*}
Working out the numerical parts we find
\begin{equation*} 36,400 + 418\ T = 2318(20-T) \end{equation*}
Solving for \(T\) gives
\begin{equation*} T = \frac{46400 - 36400}{418+2318} = 3.65^{\circ}\textrm{C}. \end{equation*}
PrevTopNext
Found typo?