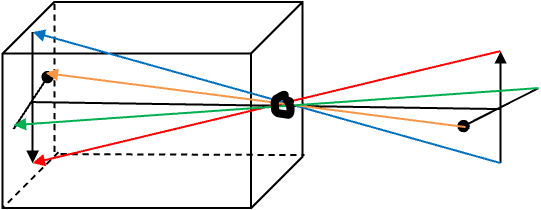
Example 45.18. Image and Angular Magnification of a Pin-hole Camera.
A \(20\text{-m}\) tall tree is at a distance of \(50\,\text{m}\) from the hole of a pinhole camera with wall \(2\,\text{m}\) from the hole. (a) How large is the image on the wall? (b) What is the angular magnification of the camera?
Answer.
(a) \(\frac{4}{5}\,\text{m}\text{,}\) (b) \(0.7\text{.}\)
Solution 1. a
Let \(d\) denote the distance to the tree, \(L\) distance to the wall. From the geometry of a pinhole camera, you can use similar triangles to get (ignoring the sign corresponding to the inversion of the image)
\begin{equation*}
\frac{h_i}{L} = \frac{h_o}{d}.
\end{equation*}
Therefore
\begin{equation*}
h_i = \frac{20}{50}\times 2 = \frac{4}{5}\,\text{m}.
\end{equation*}
Solution 2. a
The angle subtended by the image will be
\begin{equation*}
\theta_i \approx \tan\theta_i = \frac{4/5}{2}\, \text{rad}.
\end{equation*}
This small angle approx. is not quite correct. So, let us get \(\theta_i\) from arc-tan.
\begin{equation*}
\theta_i = \tan^{-1}\left( \frac{8}{5} \right) = 1.01\,\text{rad}.
\end{equation*}
We place the \(20\,\text{m}\) tree at wall at a distance \(2\,\text{m}\text{.}\) This gives
\begin{equation*}
\theta_i = \tan^{-1}\left( \frac{20}{2} \right) = 1.47\,\text{rad}.
\end{equation*}
Therefore, angular magnification will be
\begin{equation*}
M = \frac{\theta_i}{\theta_o} = \frac{1.01}{1.47} = 0.7.
\end{equation*}