Forces on Dielectrics

Section 33.6 Forces on Dielectrics

When you place a dielectric in a uniform electric field, the net force on the dielectric must be zero because the sum of forces on each dipole is zero. But, if you put a dielectric in a non-uniform electric field, there will be a net force on each dipole due to different electric field at the positive charge than on the negative charge. As a result, the dielectric will be pulled towards region of increasing electric field.

Previously we have stated that force on a dipole of dipole moment \(\vec p\) in a non-homogeneous electric field \(\vec E\) is given by

\begin{equation*} \vec F = p_x \frac{\partial \vec E}{\partial x} + p_y \frac{\partial \vec E}{\partial y} + p_z \frac{\partial \vec E}{\partial z}. \end{equation*}

For instance, if you place a dielectric at the edge of parallel plate, which have been charge by opposite charges, the non-uniformity of the field at the edge will tend to pull the dielectric.

One way to find the force on a dielectric will be to sum up forces on every microscopic dipole in the sample. This brute-force method turns out to be rather difficult to implement in practice since we usually do not know the orientation of various microscopic dipoles in the material.

An alternative method based on the following relation between a force \(\vec F\) and the work done by this force is more useful as we will now illustrate.

\begin{equation*} dW = \vec F_{\textrm{applied}} \cdot d\vec r. \end{equation*}

To find the energy associated with the electric force on the dielectric we envision applying a force that would balance the electric force as we have done when deducing the change in the potential energy. The required applied force would act in the opposite direction to the electric force \(\vec F_e\) on the dielectric and therefore they are related by

\begin{equation*} \vec F_{\textrm{applied}} =-\vec F_e. \end{equation*}

The work done by an applied force \(\vec F_{\textrm{applied}}\) would change the potential energy energy \(U\) of the dielectric body.

\begin{equation*} dW = \vec F_{\textrm{applied}}\cdot d\vec r. -\vec F \cdot d\vec r. \end{equation*}

This can be written in terms of the electric force as

\begin{equation*} dW = -\vec F_e \cdot d\vec r. \end{equation*}

The work done by the applied force changes the potential energy by amount \(dU\text{.}\) Hence the change in the potential energy of the dielectric \(dU\) is related to the electric force on the dielectric by the following equation.

\begin{equation*} dU = -\vec F_e \cdot d\vec r. \end{equation*}

For a concrete application of this result consider the displacement along the \(x\) axis of a coordinate system. In that case we will find that

\begin{equation*} dU = -\vec F_e \cdot d\vec r = -F_{x} dx, \ \ \ (x\textrm{-axis displacement only}), \end{equation*}

where \(F_{x}\) is the \(x\)-component of the electric force \(\vec F_e\) on the dielectric. Therefore, the \(x\)-component of the electric force will be related to the way the potential energy changes with the position.

\begin{equation*} F_x = -\frac{dU}{dx} \ \ \ (x\textrm{-axis displacement only}) \end{equation*}

Thus if there is a way to find the potential energy of a dielectric in a nonuniform electric field as a function of position, then we can obtain the force from this function. We now illustrate the use of this approach in a simple example of a dielectric rectangular slab being pulled between two charged parallel plates.

Example 33.22. Force on a Dielectric Slab Between Two Charged Plates.

Suppose \(\pm Q\) are on the plates separated by a distance \(d\text{.}\) Let \(w\) be the width of the plates and \(L\) their length, and at some instant, let \(L-x\) along the length have a dielectric of dielectric constant \(\epsilon_r\) and length \(x\) be empty.

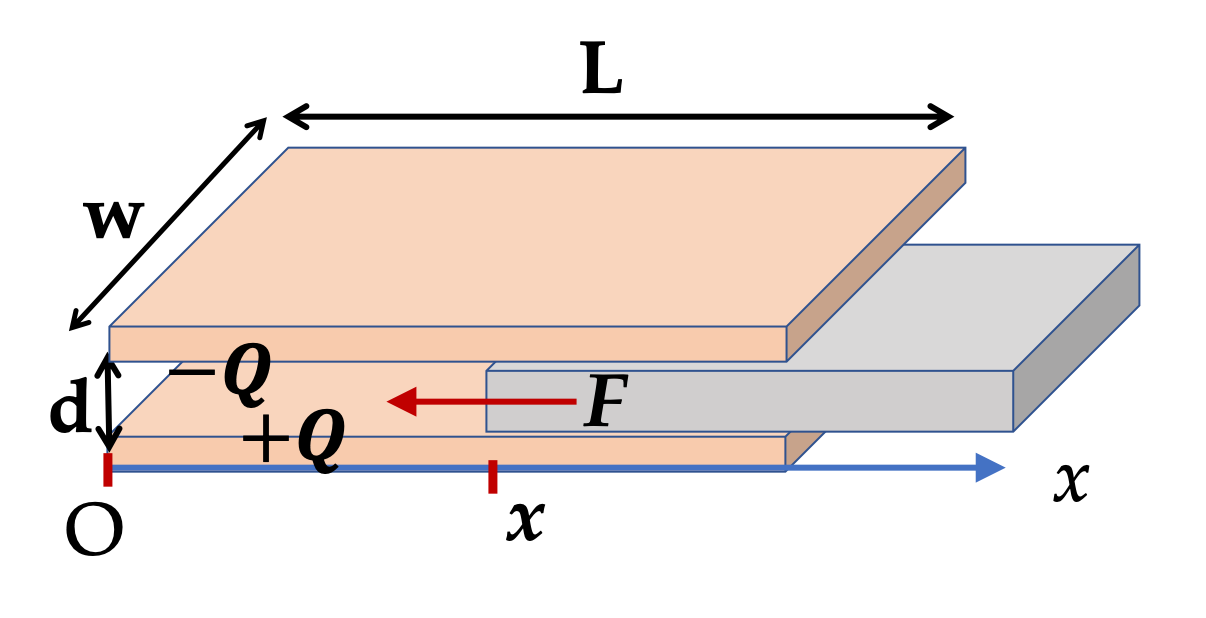
What is the force on the dielectric slab when the dielectric is partially inside the space between the plates as shown in the figure?

Solution.

To find the electric force on the dielectric slab, we need to find the expression of the potential energy as a function of the position of the slab so that we can find how the energy changes with its position.

In the chapter on capacitance, we will find the following expression for the potential energy of this entire structure as a function of the variable \(x\text{.}\)

\begin{equation*} U(x) = \frac{1}{2}\frac{Q^2}{C(x)}, \end{equation*}

with

\begin{equation*} C(x) = \frac{\epsilon_0 w . x}{d} + \frac{\epsilon_r\epsilon_0 w . (L-x)}{d}. \end{equation*}

Using \(C(x)\text{,}\) we can write \(F_x\) explicitly.

\begin{equation*} F_x = - \frac{1}{2}\ \frac{Q^2d}{\epsilon_0 w}\ \frac{\epsilon_r - 1}{\left[ x + \epsilon_r(L-x)\right]^2}. \end{equation*}

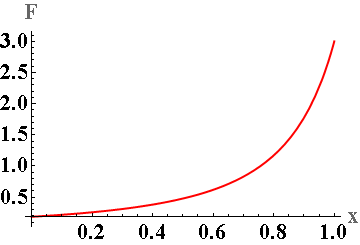
Since \(\epsilon_r \gt 1\) for dielectrics, \(F_x \lt 0\text{,}\) therefore force on the dielectric will tend to pull the dielectric inside the space between the parallel plates. Note the net force on the dipoles of the dielectric must come from the inhomogeneous fringing fields since the force on a dipole in a uniform field is zero. Figure 33.24 shows that when the entire dielectric is just outside the edge, force is greates, and as the dielectric gets pulled in further and further, the force decreases to zero when the dielectric is all the way in, which is at \(x=0\) in the plot.

Figure 33.24. Force on a dielectric as the dielectric gets pulled in. As the dielectric enters the space between the plots, near \(x=L\text{,}\) the force is strongest. The force, gradually and non-linearly, decreases to zero at the instant the dielectric is fully in as indicated at \(x=0\text{.}\) I have set \(\frac{Q^2d}{\epsilon_0 w} = 2\text{,}\) \(\epsilon_r=4\text{,}\) and \(L=1\text{.}\)

The present method based on the energy consideration avoids the calculation of fringing fields which are difficult to compute. Once the dielectric is in the uniform field region between the plates, it can be moved about without any work since there is no net electric force on a dielectric in a uniform electric field.

Prev Top Next