Length Expansion
1. Expansion of an Aluminum and a Copper Rod with Rise in Temeperature.
Follow the link: Example 20.5.
2. Gap Requirement for Train Tracks for Temperature Variations.
Follow the link: Example 20.6.
Section 20.6 Thermal Expansion Bootcamp
Exercises Exercises
Area Expansion
3. Expansion of Copper Plates When Heated.
Follow the link: Example 20.7.
4. Expansion of Copper Plates with a rectangular hole When Heated.
Follow the link: Exercise 20.2.1.
5. Fitting Rivets into Holes by Cooling the Rivets.
Follow the link: Exercise 20.2.2.
Volume Expansion
6. Expansion of Volume of Water.
Follow the link: Example 20.9.
7. Thermal Expansion of a Spherical Steel Ball.
Follow the link: Example 20.10.
Thermal Stress
8. Thermal Stress in Concrete.
Follow the link: Example 20.12.
9. Thermal Stress on Brass Cylinder.
Follow the link: Exercise 20.4.4.1.
10. Thermal Stress on Steel Bar Between Two Rigid Walls.
Follow the link: Exercise 20.4.4.2.
11. Change in Tension of a Wire with Temperature.
Follow the link: Exercise 20.4.4.3.
Miscellaneous
12. Bending Angle of a Bimetallic Strip.
A bimetallic strip of length 8 cm and thickness 1 mm at \(25^{\circ}\)C made of brass and steel is to be used for measuring the temperature. When the bimetal strip is placed in \(200^{\circ}\)C superheated steam, the strip bends such that the strip makes an arc of angle theta as shown in Figure 20.13. Find this angle.
Hint.
Work out the change in lengths of the two metals.
Answer.
\(6.9^{\circ}\text{.}\)
Solution.
Let \(s_1\) and \(s_2\) be the lengths of the two metal strips separated by thickness \(w\text{,}\) which we will assume to be same after heating as before. Let \(r_1\) and \(r_2\) be the radii of the arcs of the two metals. Here we use the subscript 1 for the metal that expands less and hence is inside part of the arc.
From the thermal expansion from the original length \(h\) we have
\begin{align*}
\amp s_1 - h = \alpha_1 h \Delta T, \\
\amp s_2 - h = \alpha_2 h \Delta T.
\end{align*}
From the geometry we have
\begin{align*}
\amp s_1= r_1 \theta, \\
\amp s_2 = r_2 \theta.
\end{align*}
Combining the two and using \(r_2-r_1 = w\) we get
\begin{equation*}
\theta = \frac{h}{w} \left(\alpha_2 - \alpha_1 \right) \Delta T.
\end{equation*}
Now, putting in the numbers we find
\begin{align*}
\theta \amp = \frac{8\ \text{cm}}{0.1\ \text{cm}}\times \frac{ \left(20.3 - 11.7 \right)\times 10^{-6}}{\ ^{\circ}\text{C}}\times 175^{\circ}\text{C},\\
\amp = 0.12\ \text{rad} = 6.9^{\circ}.
\end{align*}
13. Problem with Using Platinium-Iridium Rod for Meter.
One of the major problems with a standard of length based on a physical material such as a platinum rod is the expansion of the rod with the temperature.
We are supposed to compare other rods with the standard platinum-iridium rod which is assumed to be of a “fixed” length of 1 m. If the standard rod is 1 m at \(20^{\circ}\text{C}\text{,}\) what will be the error in assuming the the rod is still 1 m at \(27^{\circ}\text{C}\text{?}\)
Data: \(\alpha_\text{Pt/Ir} = 8.7\times 10^{-6} \text{ per deg} \text{C}\text{.}\)
Hint.
Use \(\Delta L = \alpha L \Delta T\text{.}\)
Answer.
\(0.0061\%\text{.}\)
Solution.
The absolute error will be the unaccounted-for extra length due to the thermal expansion.
\begin{align*}
\Delta L \amp= \alpha L \Delta T, \\
\amp = \frac{8.7\times 10^{-6}}{\ ^{\circ}\text{C}}\times 1\ \text{m} \times 7^{\circ}\text{C} = 61\ \mu\textrm{m}.
\end{align*}
Percentage error will be
\begin{equation*}
\dfrac{\Delta L}{L} = 61\times 10^{-6} = 0.0061\%.
\end{equation*}
14. (Calculus) Slowing of Pendulum with Rise in Temperature.
The frequency of a pendulum in a grandfather clock made of brass is related to its length \(L\) and acceleration due to gravity \(g\) of earth by the following equation.
\begin{equation*}
f = \frac{1}{2\pi}\sqrt{\frac{g}{L}}
\end{equation*}
The clock is calibrated to give the accurate time when the temperature is \(20^{\circ}\text{C}\text{.}\) How much will the clock be off in an 8 hour period when the temperature is \(30^{\circ}\text{C}\text{?}\)
Data: \(\alpha_\text{brass} = 20.3\times 10^{-6}\ \text{C}^{-1}\text{.}\)
Hint.
Use: \(\Delta f = \frac{df}{dL} \Delta L\text{.}\)
Answer.
\(0.03\ \text{s}\text{.}\)
Solution.
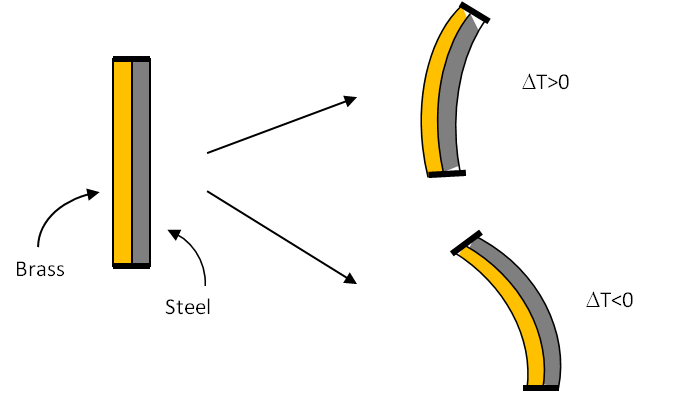
At higher temperarture, \(L\) be larger, and hence \(f\) smaller. Let \(\Delta L\) be the increase in length.
\begin{equation*}
\dfrac{\Delta L}{L} = \alpha \Delta T.
\end{equation*}
Let \(\Delta f \) be the change in frequency due to a chenge \(\Delta L\) in length. From the frequency formula we will get
\begin{align*}
\Delta f \amp = \frac{df}{dL}\, \Delta L = -\frac{1}{2}\, f\, \frac{\Delta L}{L},
\end{align*}
Therefore,
\begin{equation*}
\Delta f = -\dfrac{1}{2}\, f\, \alpha \Delta T.
\end{equation*}
Putting in the given numbers we obtain
\begin{align*}
\left| \frac{\Delta f}{f} \right| \amp = \frac{1}{2}\times \frac{20.3\times 10^{-6}}{\ ^\circ\text{C}}\times 10^{\circ}\text{C}
\end{align*}
Since \(f=1/\tau\text{,}\) where \(\tau\) is the period, the relative change in the period will be related to the relative change in frequency by
\begin{equation*}
\left|\frac{\Delta\tau}{\tau}\right| = \left|\frac{\Delta f}{f}\right| = 1.015\times 10^{-6}.
\end{equation*}
Since \(f\) will decrease, the time \(\tau\) will increase. That is, the clock will run slower. Therefore the time difference over a time period of \(8\text{ h}\) will be
\begin{equation*}
|\Delta \tau| = 1.015\times 10^{-6}\times 8\times 3600\ \text{s}= 0.03\ \text{s}.
\end{equation*}
