Skip to main content
   
Logo image

Physics Bootcamp

Samuel J. Ling

Section 43.7 Reflection and Refraction

Light rays travel in a straight line in a homogeneous tranaparent medium. At the interface of two such media, some of the light is reflected back and the rest enters the second medium, which is called refraction. The relations of the directions of the reflected and transmitted rays to that of the direction of incident lights are codified in two laws - the laws of reflection and refraction.

Subsection 43.7.1 Law of reflection

When light is incident on an interface between two media, some or all of it comes back to the first medium. The phenomenon is called reflection and the returned ray is called the reflected ray while the starting ray is called the incident ray.
Figure 43.21 shows two types of reflection - specular and diffuse. When the interface is smooth the reflected ray is sharp whose direction is symmetrical with respect to the incident ray. Such a reflection is called specular reflection, from the word Speculum for mirror in Latin. This is what happens when a visible light ray is reflected from a mirror. When the reflection is not sharp it is called a diffuse reflection, e.g. reflection from a ground glass. You are reading this book from diffuse reflected light from the paper, which makes it possible to read the same letter from different angles.
Figure 43.21. Specular and diffuse reflections. In specular reflection, only eye A is in a position to receive the reflected light while diffused reflected light can reach both eyes A and B.
As shown in Figure 43.22, the directions of incident and reflected rays are given by angles with respect to the normal to the interface. Thus, incidence angle \(\theta_1\) made by the incident ray with the normal is called the angle of incidence, and angle \(\theta_1^{\prime}\) made by the reflected ray is called the angle of reflection. The law of reflection asserts that the two angles are equal to each other.
\begin{equation} \theta_1^{\prime} = \theta_1.\tag{43.24} \end{equation}
We will try to use the common convention - add a prime to designate a reflected angle for the corresponding incident angle.
Figure 43.22. Geometric optics at an interface of two media. The figure has plane interface between two media. All angles are measured from the normal to the interface. Measuring angles with respect to the normal is a convention in which the law of refraction is written in terms of sine functions of angles rather than cosines.

Subsection 43.7.2 Law of Refraction or Snell’s Law

At the interface of two media some or the entire incident light manages to enter the second medium as shown in Figure 43.22. The light ray in the second medium is called the refracted ray. The direction of the refracted is given by the angle (\(\theta_2\)) the refracted ray makes with the normal as shown in the figure. The angle of refraction \(\theta_2\) is related to the angle of incidence and the refractive indices \(n_1\) and \(n_2\) of the two media by the law of refraction, also called the Snell’s law.
\begin{equation} n_1\ \sin\theta_1 = n_2\ \sin\theta_2.\tag{43.25} \end{equation}
According to Snell’s Law, if \(n_2 \lt n_1\) then \(\theta_2 \gt \theta_1\) and if \(n_2 \gt n_1\) then \(\theta_2 \lt \theta_1\) as shown in Figure 43.23. Remember: Higher \(n\) smaller \(\theta\). Thus, if a ray of light in air (\(n_1 = 1.0\)) is incident on water (\(n_2 = 1.33\)), it will bend towards the normal, but if a ray of light enter water from its path in glass (\(n_1 = 1.5\)), it will bend away from the normal.
Figure 43.23. Refraction at two type of interfaces. (a) Light is refracted into a medium of higher refractive index, which bends the ray towards the normal. (b) Light is refracted into a medium of lower refractive index, which bends the ray further away from the normal.

Exercises 43.7.3 Exercises

1. Rotation of Reflected Light upon Rotation of Mirror.

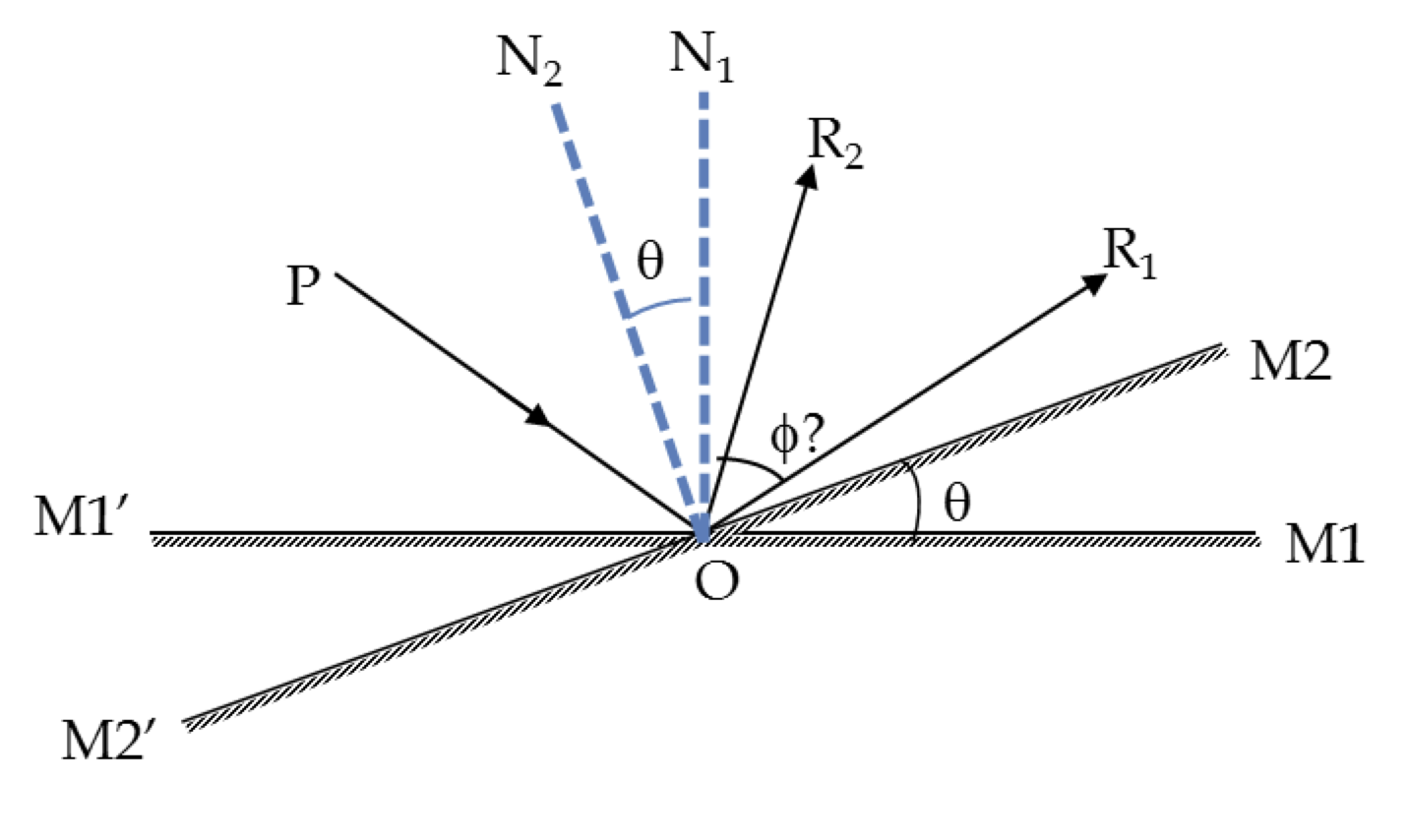
A ray of light PO is incident on a plane mirror M1 as shown in Figure 43.24. If the mirror is rotated to a new orientation M2, the reflected ray rotates from \(\text{OR}_1\) to \(\text{OR}_2\text{.}\) Find the relation between the angle of rotation of the mirror \(\angle\text{M}_1\text{OM}_2\) and the angle \(\angle\text{R}_1\text{OR}_2\text{.}\)
Figure 43.24. Figure for Exercise 43.7.3.1.
Hint.
Answer.
\(\phi = 2\theta\text{.}\)
Solution.
From the figure
\begin{align*} \amp \angle \text{PON}_1 = \angle \text{N}_1\text{OR}_1 = 90^{\circ}-\angle \text{R}_1\text{OM}_1, \\ \amp \angle \text{PON}_2 = \angle \text{N}_2\text{OR}_2 = 90^{\circ}-\angle \text{R}_2\text{OM}_2. \end{align*}
Therefore,
\begin{align*} \angle \text{PON}_1 - \angle \text{PON}_2 \amp = \angle \text{R}_2\text{OM}_2 - \angle \text{R}_1\text{OM}_1,\\ \amp = \angle \text{R}_2\text{OR}_1 + \angle \text{R}_1\text{OM}_2 -(\angle \text{R}_1\text{OM}_2 + \angle \text{M}_2\text{OM}_1),\\ \amp = \angle \text{R}_2\text{OR}_1 - \angle \text{M}_2\text{OM}_1 = \phi - \theta. \ \ \ \ \ \ (1) \end{align*}
We also have
\begin{align*} \amp \angle \text{PON}_1 = 90^{\circ}-\angle \text{P}\text{OM}_1^{\prime},\\ \amp \angle \text{PON}_2 = 90^{\circ}-\angle \text{P}\text{OM}_2^{\prime}. \end{align*}
These give
\begin{equation*} \angle \text{PON}_1 - \angle \text{PON}_2 = \angle \text{P}\text{OM}_2^{\prime}-\angle \text{P}\text{OM}_1^{\prime} = \theta.\ \ \ \ \ \ (2) \end{equation*}
From (1) and (2) we get
\begin{equation*} \phi - \theta = \theta,\ \ \ \Longrightarrow\ \ \ \phi = 2\theta. \end{equation*}

2. Refraction at Air/Water Interface.

Find the angle of refraction when light from air is incident on a water surface with an angle of incidence \(60^{\circ}\text{.}\)
Hint.
Use Snell’s law.
Answer.
\(41^{\circ}\text{.}\)
Solution.
We use Snell’s law, \(n_1\, \sin\theta_1 = n_2\, \sin\theta_2\text{.}\) Here \(n_1 = 1\text{,}\) \(n_2 = \frac{4}{3}\text{,}\) \(\theta_1 = 60^{\circ}\text{.}\) Therefore,
\begin{equation*} \theta_2 = \sin^{-1}\left(\frac{n_1}{n_2}\sin\theta_1 \right) = 41^{\circ}. \end{equation*}

3. Light Bending from a Bulb Immersed in Water.

A light bulb is immersed inside a water tank. A ray of light from the bulb is incident on the water/air interface at an angle of \(65^\circ\) from the horizontal interface. At what angle from the normal does the ray come out in the air?
Hint.
Use Snell’s law.
Answer.
\(34.3^\circ\) from normal.
Solution.
\begin{align*} \theta_1 \amp = 90^{\circ}-65^{\circ} = 25^{\circ}.\\ \theta_2 \amp = \sin^{-1}\left( \dfrac{n_1\sin\theta_1}{n_2}\right)\\ \amp = \sin^{-1}\left( \dfrac{\frac{4}{3}\sin25^{\circ}}{1}\right) = 34.3^{\circ}. \end{align*}

4. Lateral Displacment of a Ray when Traversing a Rectangular Plate.

A ray of light is incident at \(30^\circ\) to the normal on a rectangular glass plate of width \(5\text{ cm}\text{,}\) and emerges on the other side (see Figure 43.25 ). Find (a) the direction of the emergent ray, and (b) the lateral displacement from the original direction. Use \(n = 1.5\) for glass.
Figure 43.25. figure for Exercise 43.7.3.4.
Hint.
First draw ray diagram for the two refraction points for the ray. Then find angle of refraction at the first refraction.
Answer.
\(d = 0.97\text{ cm}\text{.}\)
Solution.
The ray through the glass plate is shown in the figure below. The ray exiting the other end of the rectangular plate at A would be parallel to the incident ray at P. Let \(\theta\) be the angle of refraction at point P.
\begin{equation*} \theta = \sin^{-1}\left( \dfrac{1\times \sin\:30^{\circ}}{1.5}\right) = 19.5^{\circ}. \end{equation*}
Therefore, the distance OA and OB will be
\begin{align*} \amp \text{OA} = (5\:\text{cm})\:\tan\:19.5^{\circ} = 1.77\:\text{cm}.\\ \amp \text{OB} = (5\:\text{cm})\:\tan\:30^{\circ} = 2.89\:\text{cm}. \end{align*}
Now, in the triangle \(\angle\text{ABC} = 30^{\circ}\text{.}\) Therefore,
\begin{equation*} \text{BC} = \text{AB}\:\cos\:30^{\circ} = 0.97\:\text{cm}. \end{equation*}

5. Separation of Two Rays of Different Frequencies when Traversing a Rectangular Plate.

A ray of light consisting of two wavelengths of light (\(700\text{ nm}\) and \(400\text{ nm}\) in air) is incident at \(30^\circ\) to the normal on a rectangular flint glass plate of width \(5\text{ cm}\text{,}\) and emerges on the other side as shown in Figure 43.25 of Exercise 43.7.3.4. The refractive indices of flint glass for \(700\text{-nm}\) and \(400\text{-nm}\) light are \(1.62\) and \(1.67\) respectively.
Find (a) direction(s) of the emergent ray, and (b) the lateral displacement(s) d from the original direction. (c) Using a protractor and a ruler, draw as accurately as you can the rays you found in exercise above.
Hint.
Find displacements of each ray separately as in Exercise 43.7.3.4.
Answer.
\(d_{\text{R}} = 1.09\text{ cm}\text{,}\) \(d_{\text{B}} = 1.14\text{ cm}\text{.}\)
Solution.
Refer to the figures in the Exercise 43.7.3.4. There will be one such ray for each color. Let \(\theta = \theta_{\text{R}}\) for the red light of wavelength \(700\text{ nm}\) and \(\theta = \theta_{\text{B}}\) for the blue light of wavelength \(400\text{ nm}\text{.}\) These angles in glass will be
\begin{align*} \amp \theta_{\text{R}} = \sin^{-1}\left( \dfrac{1\times \sin\:30^{\circ}}{1.62}\right) = 18^{\circ}.\\ \amp \theta_{\text{B}} = \sin^{-1}\left( \dfrac{1\times \sin\:30^{\circ}}{1.67}\right) = 17.4^{\circ}. \end{align*}
The displacemets of the two rays when they exit on the other side would be \(d = d_{\text{R}}\) and \(d = d_{\text{B}}\) given by
\begin{align*} \amp d_{\text{R}} = (5\:\text{cm})\:\left( \tan\:30^{\circ} - \tan\:18^{\circ}\right)\:\cos\:30^{\circ} = 1.09\:\text{cm}.\\ \amp d_{\text{B}} = (5\:\text{cm})\:\left( \tan\:30^{\circ} - \tan\:17.4^{\circ}\right)\:\cos\:30^{\circ} = 1.14\:\text{cm}. \end{align*}
PrevTopNext
Found typo?